28 releases (14 stable)
Uses new Rust 2024
| 1.7.0 | Apr 6, 2025 |
|---|---|
| 1.5.0 | Feb 5, 2025 |
| 1.4.1 | Dec 27, 2024 |
| 1.4.0 | Aug 29, 2024 |
| 0.1.7 | Jul 25, 2023 |
#88 in Algorithms
740 downloads per month
Used in 5 crates
(3 directly)
130KB
1.5K
SLoC
orx-priority-queue
Priority queue traits and high performance d-ary heap implementations.
no-std: This crate supports no-std; however, std is added as a default feature. Please include with no-default-features for no-std use cases:
cargo add orx-priority-queue --no-default-features.
A. Priority Queue Traits
This crate aims to provide algorithms with the abstraction over priority queues. In order to achieve this, two traits are defined: PriorityQueue<N, K> and PriorityQueueDecKey<N, K>. The prior is a simple queue while the latter extends it by providing additional methods to change priorities of the items that already exist in the queue.
The separation is important since additional operations often requires the implementors to allocate internal memory for bookkeeping. Therefore, we would prefer PriorityQueueDecKey<N, K> only when we need to change the priorities.
See DecreaseKey section for a discussion on when decrease-key operations are required and why they are important.
B. d-ary Heap Implementations
d-ary implementations are generalizations of the binary heap; i.e., binary heap is a special case where D=2. It is advantageous to have a parametrized d; as for instance, in the benchmarks defined here, D=4 outperforms D=2.
- With a large d: number of per level comparisons increases while the tree depth becomes smaller.
- With a small d: each level requires fewer comparisons while the tree with the same number of nodes is deeper.
Further, three categories of d-ary heap implementations are introduced.
1. DaryHeap (PriorityQueue)
This is the basic d-ary heap implementing PriorityQueue. It is the default choice unless priority updates or decrease-key operations are required.
2. DaryHeapOfIndices (PriorityQueue + PriorityQueueDecKey)
This is a d-ary heap paired up with a positions array and implements PriorityQueueDecKey.
- It requires the nodes to implement
HasIndextrait which is nothing butfn index(&self) -> usize. Note thatusize,u64, etc., already implementsHasIndex. - Further, it requires to know the maximum index that is expected to enter the queue. In other words, candidates are expected to come from a closed set.
Once these conditions are satisfied, it performs significantly faster than the alternative decrease key queues.
Although the closed set requirement might sound strong, it is often naturally satisfied in mathematical algorithms. For instance, for most network traversal algorithms, the candidates set is the nodes of the graph, or indices in 0..num_nodes. Similarly, if the heap is used to be used for sorting elements of a list, indices are simply coming from 0..list_len.
This is the default decrease-key queue provided that the requirements are satisfied.
3. DaryHeapWithMap (PriorityQueue + PriorityQueueDecKey)
This is a d-ary heap paired up with a positions map (HashMap or BTreeMap when no-std) and also implements PriorityQueueDecKey.
This is the most general decrease-key queue that provides the open-set flexibility and fits to almost all cases.
Other Queues
In addition, queue implementations are provided in this crate for the following external data structures:
std::collections::BinaryHeap<(N, K)>implements onlyPriorityQueue<N, K>,priority_queue:PriorityQueue<N, K>implements bothPriorityQueue<N, K>andPriorityQueueDecKey<N, K>- requires
--features impl_priority_queue - or
--features impl_all
- requires
This allows to use all the queue implementations interchangeably and pick the one fitting best to the use case.
Performance & Benchmarks
You may find the details of the benchmarks at benches folder.
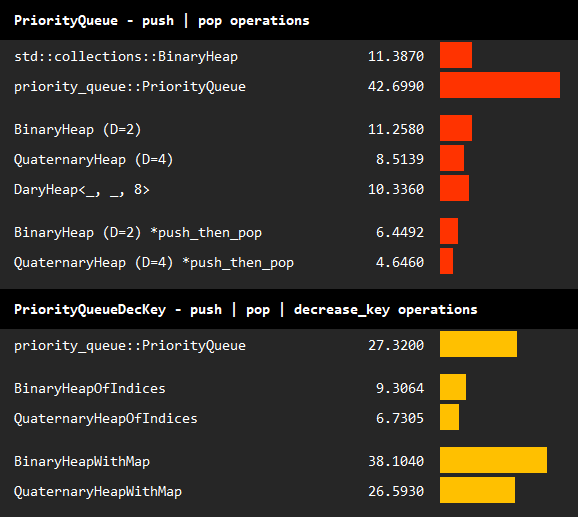
The table above summarizes the benchmark results of basic operations on basic queues, and queues allowing decrease key operations.
- In the first benchmark, we repeatedly call
pushandpopoperations on a queue while maintaining an average length of 100000:- We observe that
BinaryHeap(DaryHeap<_, _, 2>) performs almost the same as the standard binary heap. - Experiments on different values of d shows that
QuaternaryHeap(D=4) outperforms both binary heaps. - Further increasing D to 8 does not improve performance.
- Finally, we repeat the experiments with
BinaryHeapandQuaternaryHeapusing the specializedpush_then_popoperation. Note that this operation further doubles the performance, and hence, should be used whenever it fits the use case.
- We observe that
- In the second benchmark, we add
decrease_key_or_pushcalls to the operations. Standard binary heap is excluded since it cannot implementPriorityQueueDecKey.- We observe that
DaryHeapOfIndicessignificantly outperforms other decrease key queues. - Among
BinaryHeapOfIndicesandQuaternaryHeapOfIndices, the latter with D=4 again performs better.
- We observe that
C. Examples
C.1. Basic Usage
Below example demonstrates basic usage of a simple PriorityQueue. You may see the entire functionalities here.
use orx_priority_queue::*;
// generic over simple priority queues
fn test_priority_queue<P>(mut pq: P)
where
P: PriorityQueue<usize, f64>,
{
pq.clear();
pq.push(0, 42.0);
assert_eq!(Some(&0), pq.peek().map(|x| x.node()));
assert_eq!(Some(&42.0), pq.peek().map(|x| x.key()));
let popped = pq.pop();
assert_eq!(Some((0, 42.0)), popped);
assert!(pq.is_empty());
pq.push(0, 42.0);
pq.push(1, 7.0);
pq.push(2, 24.0);
pq.push(10, 3.0);
while let Some(popped) = pq.pop() {
println!("pop {:?}", popped);
}
}
// d-ary heap generic over const d
const D: usize = 4;
test_priority_queue(DaryHeap::<usize, f64, D>::default());
test_priority_queue(DaryHeapWithMap::<usize, f64, D>::default());
test_priority_queue(DaryHeapOfIndices::<usize, f64, D>::with_index_bound(100));
// type aliases for common heaps: Binary or Quaternary
test_priority_queue(BinaryHeap::default());
test_priority_queue(QuaternaryHeapWithMap::default());
test_priority_queue(BinaryHeapOfIndices::with_index_bound(100));
As mentioned, PriorityQueueDecKey extends capabilities of a PriorityQueue. You may see the additional functionalities here.
use orx_priority_queue::*;
// generic over decrease-key priority queues
fn test_priority_queue_deckey<P>(mut pq: P)
where
P: PriorityQueueDecKey<usize, f64>,
{
pq.clear();
pq.push(0, 42.0);
assert_eq!(Some(&0), pq.peek().map(|x| x.node()));
assert_eq!(Some(&42.0), pq.peek().map(|x| x.key()));
let popped = pq.pop();
assert_eq!(Some((0, 42.0)), popped);
assert!(pq.is_empty());
pq.push(0, 42.0);
assert!(pq.contains(&0));
pq.decrease_key(&0, 7.0);
assert_eq!(Some(&0), pq.peek().map(|x| x.node()));
assert_eq!(Some(&7.0), pq.peek().map(|x| x.key()));
let deckey_result = pq.try_decrease_key(&0, 10.0);
assert!(matches!(ResTryDecreaseKey::Unchanged, deckey_result));
assert_eq!(Some(&0), pq.peek().map(|x| x.node()));
assert_eq!(Some(&7.0), pq.peek().map(|x| x.key()));
while let Some(popped) = pq.pop() {
println!("pop {:?}", popped);
}
}
// d-ary heap generic over const d
const D: usize = 4;
test_priority_queue_deckey(DaryHeapOfIndices::<usize, f64, D>::with_index_bound(100));
test_priority_queue_deckey(DaryHeapWithMap::<usize, f64, D>::default());
// type aliases for common heaps: Binary or Quaternary
test_priority_queue_deckey(BinaryHeapOfIndices::with_index_bound(100));
test_priority_queue_deckey(QuaternaryHeapWithMap::default());
C.2. Usage in Dijkstra's Shortest Path
You may see below two implementations of the Dijkstra's shortest path algorithm: one using a PriorityQueue and the other with a PriorityQueueDecKey. Please note the following:
- Priority queue traits allow us to be generic over queues. Therefore, we are able to implement the algorithm once that works for any queue implementation.
- The second implementation with a decrease key queue pushes some of the bookkeeping to the queue, and arguably leads to a cleaner algorithm implementation.
use orx_priority_queue::*;
pub struct Edge {
head: usize,
weight: u32,
}
pub struct Graph(Vec<Vec<Edge>>);
impl Graph {
fn num_nodes(&self) -> usize {
self.0.len()
}
fn out_edges(&self, node: usize) -> impl Iterator<Item = &Edge> {
self.0[node].iter()
}
}
// Implementation using a PriorityQueue
fn dijkstras_with_basic_pq<Q: PriorityQueue<usize, u32>>(
graph: &Graph,
queue: &mut Q,
source: usize,
sink: usize,
) -> Option<u32> {
// init
queue.clear();
let mut dist = vec![u32::MAX; graph.num_nodes()];
dist[source] = 0;
queue.push(source, 0);
// iterate
while let Some((node, cost)) = queue.pop() {
if node == sink {
return Some(cost);
} else if cost > dist[node] {
continue;
}
let out_edges = graph.out_edges(node);
for Edge { head, weight } in out_edges {
let next_cost = cost + weight;
if next_cost < dist[*head] {
queue.push(*head, next_cost);
dist[*head] = next_cost;
}
}
}
None
}
// Implementation using a PriorityQueueDecKey
fn dijkstras_with_deckey_pq<Q: PriorityQueueDecKey<usize, u32>>(
graph: &Graph,
queue: &mut Q,
source: usize,
sink: usize,
) -> Option<u32> {
// init
queue.clear();
let mut visited = vec![false; graph.num_nodes()];
// init
visited[source] = true;
queue.push(source, 0);
// iterate
while let Some((node, cost)) = queue.pop() {
if node == sink {
return Some(cost);
}
let out_edges = graph.out_edges(node);
for Edge { head, weight } in out_edges {
if !visited[*head] {
queue.try_decrease_key_or_push(&head, cost + weight);
}
}
visited[node] = true;
}
None
}
// example input
let e = |head: usize, weight: u32| Edge { head, weight };
let graph = Graph(vec![
vec![e(1, 4), e(2, 5)],
vec![e(0, 3), e(2, 6), e(3, 1)],
vec![e(1, 3), e(3, 9)],
vec![],
]);
// TESTS: basic priority queues
let mut pq = BinaryHeap::new();
assert_eq!(Some(5), dijkstras_with_basic_pq(&graph, &mut pq, 0, 3));
assert_eq!(None, dijkstras_with_basic_pq(&graph, &mut pq, 3, 1));
let mut pq = QuaternaryHeap::new();
assert_eq!(Some(5), dijkstras_with_basic_pq(&graph, &mut pq, 0, 3));
assert_eq!(None, dijkstras_with_basic_pq(&graph, &mut pq, 3, 1));
let mut pq = DaryHeap::<_, _, 8>::new();
assert_eq!(Some(5), dijkstras_with_basic_pq(&graph, &mut pq, 0, 3));
assert_eq!(None, dijkstras_with_basic_pq(&graph, &mut pq, 3, 1));
// TESTS: decrease key priority queues
let mut pq = BinaryHeapOfIndices::with_index_bound(graph.num_nodes());
assert_eq!(Some(5), dijkstras_with_deckey_pq(&graph, &mut pq, 0, 3));
assert_eq!(None, dijkstras_with_deckey_pq(&graph, &mut pq, 3, 1));
let mut pq = DaryHeapOfIndices::<_, _, 8>::with_index_bound(graph.num_nodes());
assert_eq!(Some(5), dijkstras_with_deckey_pq(&graph, &mut pq, 0, 3));
assert_eq!(None, dijkstras_with_deckey_pq(&graph, &mut pq, 3, 1));
let mut pq = BinaryHeapWithMap::new();
assert_eq!(Some(5), dijkstras_with_deckey_pq(&graph, &mut pq, 0, 3));
assert_eq!(None, dijkstras_with_deckey_pq(&graph, &mut pq, 3, 1));
Contributing
Contributions are welcome! If you notice an error, have a question or think something could be improved, please open an issue or create a PR.
License
Dual-licensed under Apache 2.0 or MIT.