77 releases (46 stable)
Uses new Rust 2024
| new 3.17.0 | May 17, 2025 |
|---|---|
| 3.15.0 | Feb 11, 2025 |
| 3.11.0 | Dec 12, 2024 |
| 3.10.0 | Sep 20, 2024 |
| 0.9.2 | Sep 10, 2023 |
#68 in Data structures
4,058 downloads per month
Used in 14 crates
(11 directly)
365KB
8K
SLoC
orx-split-vec
An efficient dynamic capacity vector with pinned element guarantees.
A SplitVec implements PinnedVec; you may read the detailed information about pinned element guarantees and why they are useful in the motivation-and-examples section. In brief, a pinned vector does not allow implicit changes in memory locations of its elements; such as moving the entire vector to another memory location due to additional capacity requirement.
Growth and Capacity Decisions
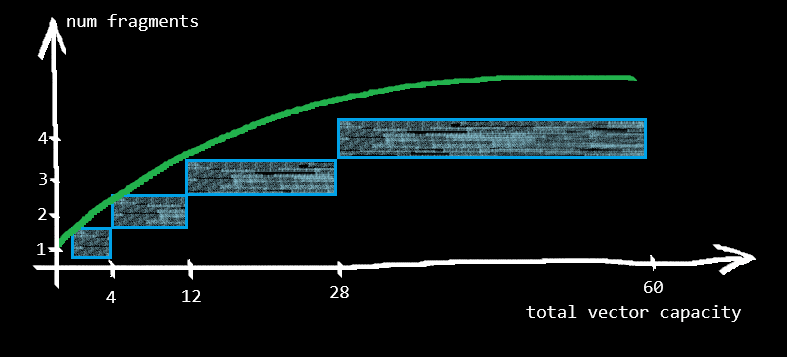
As the name suggests, a split vector is a collection of fragments. Each fragment is a contiguous memory chunk used to store elements. Unlike standard vectors, a fragment's capacity never changes. However, the fragments of a split vector might have different capacities. The decision on the capacity of the next fragment to be allocated is decided by the Growth strategy. Notice that the split vector has two generic parameters: the element type and the growth strategy; i.e., SplitVec<T, G: Growth>.
Defining a growth strategy is straightforward, there exists one required method:
fn new_fragment_capacity_from(
&self,
fragment_capacities: impl ExactSizeIterator<Item = usize>,
) -> usize;
The strategy must decide:
- what the first fragment's capacity must be when the
fragment_capacitiesis empty, and - given the prior
fragment_capacities, what the next fragment's capacity must be.
One can define a custom growth strategy and use it with the split vector. This crate provides three efficient growth strategy implementations that are useful in different situations.
Doubling
This is the default growth strategy; i.e., SplitVec<T> is equivalent to SplitVec<T, Doubling>. With Doubling strategy:
- the first fragment will hold 4 elements,
- the second fragment will hold 8 elements,
- the third fragment will hold 16 elements,
- and so on.
In addition to Growth, Doubling strategy also implements GrowthWithConstantTimeAccess. In other words, it provides constant time random access to elements.
Its sequential access performance is close to that of the standard vector since the impact of fragmentation diminishes and converges to zero as the size of the vector grows.
Linear
This strategy leads to a (stepwise) linear growth of the total vector capacity:
- the first fragment will hold n elements,
- the second fragment will hold n elements,
- the third fragment will hold n elements,
- and so on.
Therefore, for creating a split vector with linear growth, we are required to explicitly provide the fixed fragment capacity n (hence, it does not implement Default).
This strategy gives the caller better control on memory usage and is specifically useful when memory is more valuable or scarcer. The impact of fragmentation on sequential access is again up to the caller since n directly defines how many contiguous fragments will exist.
Linear strategy also implements GrowthWithConstantTimeAccess providing constant time random access to elements.

Recursive
Recursive strategy is a specialized variant of the Doubling, which works identical unless at some point extend method is called on the vector. The extend operation of a SplitVec with recursive growth strategy is a constant time operation. This makes it appealing for recursive data structures such as linked lists or trees; hence the name. Consider for instance extending a tree by appending another tree to its leaf. Recursive strategy aims to perform this operation in O(1).
It is equivalent to Doubling strategy in terms of sequential access performance. However, due to the additional flexibility, it cannot implement GrowthWithConstantTimeAccess. Its random access time complexity is O(f) where f is the number of fragments in the split vector.
Parallelization
SplitVec implements ConcurrentCollection for all above-mentioned growth strategies.
Therefore, when orx_parallel crate is included, SplitVec also automatically implements ParallelizableCollection.
This means that computations over the split vector can be efficiently parallelized:
split_vec.par()returns a parallel iterator over references to its elements, andsplit_vec.into_par()consumes the vector and returns a parallel iterator of the owned elements.
You may find demonstrations in demo_parallelization and bench_parallelization examples.
Examples
SplitVec api resembles and aims to cover as much as possible the standard vector's api.
use orx_split_vec::*;
let mut vec = SplitVec::new();
vec.push(0);
vec.extend_from_slice(&[1, 2, 3]);
assert_eq!(vec, &[0, 1, 2, 3]);
vec[0] = 10;
assert_eq!(10, vec[0]);
vec.remove(0);
vec.insert(0, 0);
assert_eq!(6, vec.iter().sum());
assert_eq!(vec.clone(), vec);
let std_vec: Vec<_> = vec.into();
assert_eq!(&std_vec, &[0, 1, 2, 3]);
Naturally, it has certain specific differences and operations. For instance, we cannot have as_slice method for the split vector since it is not a single big chunk of memory. Instead, we have the slices, slices_mut and try_get_slice methods.
use orx_split_vec::*;
#[derive(Clone)]
struct MyCustomGrowth;
impl Growth for MyCustomGrowth {
fn new_fragment_capacity_from(&self, fragment_capacities: impl ExactSizeIterator<Item = usize>) -> usize {
fragment_capacities.last().map(|f| f + 1).unwrap_or(4)
}
}
impl PseudoDefault for MyCustomGrowth {
fn pseudo_default() -> Self {
MyCustomGrowth
}
}
// set the growth explicitly
let vec: SplitVec<i32, Linear> = SplitVec::with_linear_growth(4);
let vec: SplitVec<i32, Doubling> = SplitVec::with_doubling_growth();
let vec: SplitVec<i32, MyCustomGrowth> = SplitVec::with_growth(MyCustomGrowth);
// methods revealing fragments
let mut vec = SplitVec::with_doubling_growth();
vec.extend_from_slice(&[0, 1, 2, 3]);
assert_eq!(4, vec.capacity());
assert_eq!(1, vec.fragments().len());
vec.push(4);
assert_eq!(vec, &[0, 1, 2, 3, 4]);
assert_eq!(2, vec.fragments().len());
assert_eq!(4 + 8, vec.capacity());
// SplitVec is not contiguous; instead a collection of contiguous fragments
// so it might or might not return a slice for a given range
let slice: SplitVecSlice<_> = vec.try_get_slice(1..3);
assert_eq!(slice, SplitVecSlice::Ok(&[1, 2]));
let slice = vec.try_get_slice(3..5);
// the slice spans from fragment 0 to fragment 1
assert_eq!(slice, SplitVecSlice::Fragmented(0, 1));
let slice = vec.try_get_slice(3..7);
assert_eq!(slice, SplitVecSlice::OutOfBounds);
// instead of a single slice; we can get an iterator of slices
let mut slices = vec.slices(..);
assert_eq!(2, slices.len());
assert_eq!(slices.next().unwrap(), &[0, 1, 2, 3]);
assert_eq!(slices.next().unwrap(), &[4]);
let mut slices = vec.slices(0..3);
assert_eq!(1, slices.len());
assert_eq!(slices.next().unwrap(), &[0, 1, 2]);
let mut slices = vec.slices(3..5);
assert_eq!(2, slices.len());
assert_eq!(slices.next().unwrap(), &[3]);
assert_eq!(slices.next().unwrap(), &[4]);
Finally, its main difference and objective is to provide pinned element guarantees as demonstrated in the example below.
use orx_split_vec::*;
let mut vec = SplitVec::new(); // Doubling growth as the default strategy
// split vec with 1 item in 1 fragment
vec.push(42usize);
assert_eq!(&[42], &vec);
assert_eq!(1, vec.fragments().len());
assert_eq!(&[42], &vec.fragments()[0]);
// let's get a pointer to the first element to test later
let addr42 = &vec[0] as *const usize;
// let's push 3 + 8 + 16 new elements to end up with 3 fragments
for i in 1..(3 + 8 + 16) {
vec.push(i);
}
for (i, elem) in vec.iter().enumerate() {
assert_eq!(if i == 0 { 42 } else { i }, *elem);
}
assert_eq!(3, vec.fragments().len());
// the memory location of the first element remains intact
assert_eq!(addr42, &vec[0] as *const usize);
// we can safely dereference it and read the correct value
// of course, dereferencing is still through the unsafe api,
// however, the guarantee allows for safe api's for wrapper types such as
// ConcurrentVec, ImpVec, SelfRefCol
assert_eq!(unsafe { *addr42 }, 42);
Benchmarks
Recall that the motivation of using a split vector is to provide pinned element guarantees. However, it is also important to keep the performance within an acceptable range compared to the standard vector. Growth strategies implemented in this crate achieve this goal.
Benchmark: Growth
You may see the benchmark at benches/grow.rs.
The benchmark compares the build up time of vectors by pushing elements one by one. The baseline is the standard vector created by Vec::with_capacity which has the perfect information on the number of elements to be pushed. Compared variants are vectors created with no prior knowledge about capacity: Vec::new, SplitVec<_, Linear> and SplitVec<_, Doubling>.
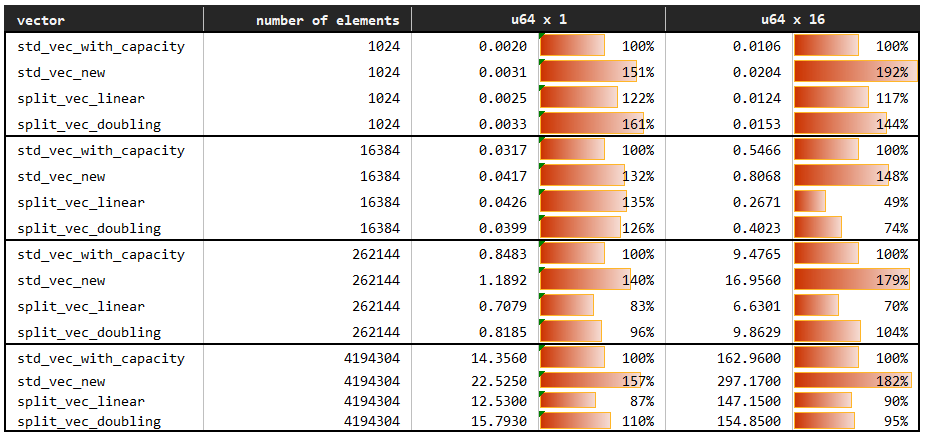
The baseline Vec::with_capacity performs between 1.5 and 2.0 times faster than Vec::new. SplitVec variants also do not use prior knowledge about the number of elements to be pushed; however, it has the advantage of copy-free growth. Overall, its growth performance is much closer to standard vector with perfect capacity information than that of the Vec::new.
Recursive strategy is omitted here since it behaves exactly as the Doubling strategy in the growth scenario.
Benchmark: Random Access
You may see the benchmark at benches/random_access.rs.
In this benchmark, we access vector elements by indices in a random order. The baseline standard vector is compared to Linear and Doubling growth strategies that allow for constant time random access. Recursive strategy without constant time random access is also included in the experimentation.

We can see that Linear is slower than Doubling. Random access performance of Doubling is at most 40% slower than that of the standard vector, and the difference diminishes as the element size or number of elements gets larger.
Recursive, on the other hand, is between 5 and 7 times slower for small elements and around 1.5 times slower for larger structs.
Benchmark: Serial Access
You may see the benchmark at benches/serial_access.rs.
Here, we benchmark the case where we access each element of the vector in order starting from the first element to the last. Baseline Vec is compared with Doubling, Linear and Recursive growth strategies; however, SplitVec actually uses the same iterator to allow for the serial access for any growth strategy. The difference, if any, stems from the sizes of fragments and their impact on cache locality.
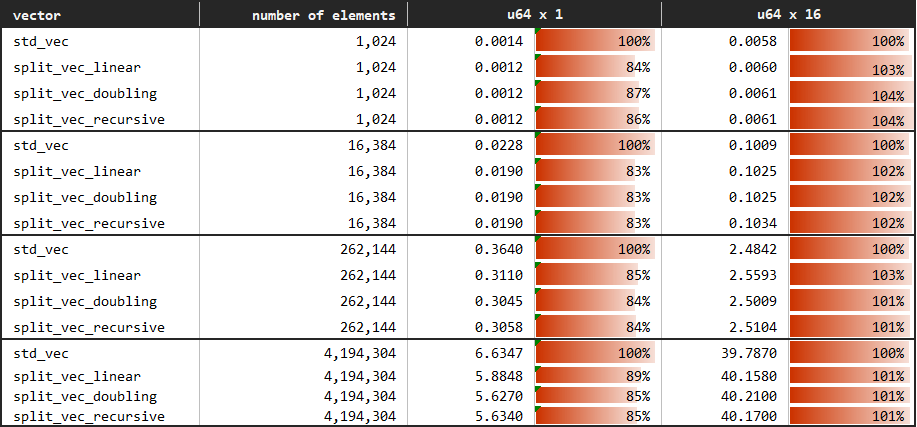
We observe that split vector performance is almost identical to that of the standard vector. Although there are minor deviations, we do not observe any significant difference among tested growth strategies.
Benchmark: Append
You may see the benchmark at benches/serial_access.rs.
Appending vector to another vector is a critical operation for certain use cases. One example is recursive data structures such as trees or linked lists. Consider appending a tree to the leaf of another tree to get a new merged tree. This operation could be handled by copying data around to maintain a certain structure or by simply accepting the incoming chunk in constant time.
- Vec,
SplitVec<_, Doubling>andSplitVec<_, Linear>perform memory copies in order to keep their internal structure which allows for efficient random access. SplitVec<_, Recursive>, on the other hand, utilizes its fragmented structure and accepts the incoming chunk as it is. Hence, appending another vector to it is simply no-ops. This does not degrade serial access performance. However, it leads to slower random access as we observe in the previous benchmark.
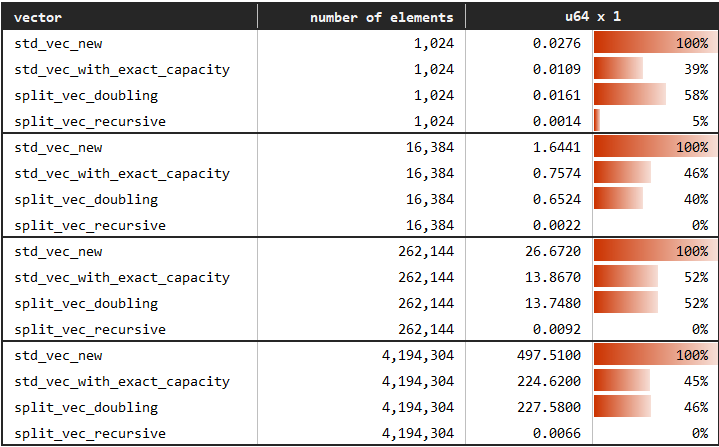
Further, SplitVec<T, Doubling> is around twice faster than Vec::new when we do not have any prior information about the required capacity. When we have perfect information and create the standard vector with Vec::with_capacity, standard vector and SplitVec perform equivalently.
Contributing
Contributions are welcome! If you notice an error, have a question or think something could be improved, please open an issue or create a PR.
License
Dual-licensed under Apache 2.0 or MIT.