9 releases
| 0.2.12 | Sep 20, 2024 |
|---|---|
| 0.2.11 | Sep 20, 2024 |
| 0.2.10 | May 28, 2024 |
| 0.2.8 | Oct 16, 2023 |
| 0.1.4 | Oct 24, 2022 |
#26 in Science
26 downloads per month
Used in 2 crates
(via qecp)
1.5MB
23K
SLoC
Fusion Blossom
A fast Minimum-Weight Perfect Matching (MWPM) solver for Quantum Error Correction (QEC)
Please see our tutorial for a quick explanation and some Python demos.
Our paper is out on arXiv! https://arxiv.org/abs/2305.08307
Key Features
- Correctness: This is an exact MWPM solver, verified against the Blossom V library with millions of randomized test cases .
- Linear Complexity: The average decoding time is roughly $O(N)$ given small physical error rate, proportional to the number of defect vertices $N$.
- Parallelism: A single MWPM decoding problem can be partitioned and solved in parallel, then fused together to find an exact global MWPM solution.
- Simple Interface: The graph problem is abstracted and easy-to-use for QEC applications. Especially, it supports decoding erasure errors (by setting some edge weights to 0 on the fly).
Benchmark Highlights
- In circuit-level noise model with $p$ = 0.001, code distance $d$ = 21, rotated CSS code, 100000 measurement rounds
- single-thread: 3.9us per defect vertex or 13us per measurement round
- 64-threads: 95ns per defect vertex or 0.3us per measurement round
- in streaming mode, the latency is 0.7ms regardless of rounds of measurement
Background and Key Ideas
MWPM decoders are widely known for its high accuracy [1] and several optimizations that further improves its accuracy [2]. However, there weren't many publications that improve the speed of the MWPM decoder over the past 10 years. Fowler implemented an $O(N)$ asymptotic complexity MWPM decoder in [3] and proposed an $O(1)$ complexity parallel MWPM decoder in [4], but none of these are publicly available to our best knowledge. Higgott implemented a fast but approximate MWPM decoder (namely "local matching") with roughly $O(N)$ complexity in [5]. With recent experiments of successful QEC on real hardware, it's time for a fast and accurate MWPM decoder to become available to the community.
Our idea comes from our study on the Union-Find (UF) decoder [6]. UF decoder is a fast decoder with $O(N)$ worst-case time complexity, at the cost of being less accurate compared to the MWPM decoder. Inspired by the Fowler's diagram [3], we found a relationship between the UF decoder [7]. This nice animation (press space to trigger animation) could help people see the analogy between UF and MWPM decoders. With this interpretation, we're able to combind the strength of UF and MWPM decoders together.
- From the UF decoder, we learnt to use a sparse decoding graph representation for fast speed
- From the MWPM decoder, we learnt to find an exact minimum-weight perfect matching for high accuracy
We shall note that Oscar Higgott and Craig Gidney independently reach the same approach of using sparse decoding graph to solve MWPM more efficiently in PyMatching V2 [8]. It's impressive to see that they have much better single-thread performance than fusion-blossom (about 5x-20x speedup). They use more optimizations like priority queue that appears in existing literature of blossom algorithms (check their paper at [9]). Also, they use C++ language rather than Rust programming language. Rust enforces memory safety which adds some runtime overhead (like vector boundary check and unnecessary locks in parallel programming). We use unsafe Rust to improve the speed by 1.5x-3x but these features are not yet enabled in the Python library and only available when using the native Rust library. In fact, PyMatching V2's optimizations and fusion-blossom's parallel computation (fusion operation) are compatible with each other. With their impressive work, we're looking forward to another 5x-20x speed of the parallel MWPM decoder if combined together. For now, user should use PyMatching for better CPU efficiency in large-scale simulations, and use fusion-blossom library as an educational tool with visualization tool and entry-level tutorials.
Demo
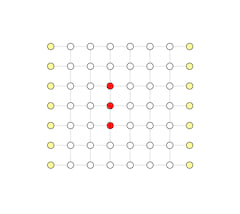
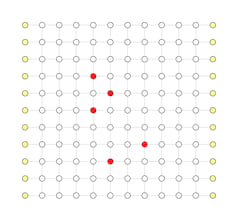
We highly suggest you watch through several demos here to get a sense of how the algorithm works. All our demos are captured from real algorithm execution. In fact, we're showing you the visualized debugger tool we wrote for fusion blossom. The demo is a 3D website and you can control the view point as you like.
Click the demo image below to view the corresponding demo
Serial Execution
Parallel Execution (Shown in Serial For Better Visual)
Usage
Our code is written in Rust programming language for speed and memory safety, but it's hardly an easy language to learn. To make the decoder more accessible, we bind the library to Python and user can simply install the library using pip3 install fusion-blossom.
We have several Python demos at the tutorial website . Also there is a simple example for decoder, and you can run it by cloning the project and run python3 scripts/demo.py.
For parallel solver, it needs user to provide a partition strategy. Please check our paper for a thorough description of how partition works.
Interface
Sparse Decoding Graph and Integer Weights
The weights in QEC decoding graph are computed by taking the log of error probability, e.g. $w_e = \log{(1-p)/p}$ or roughly $w_e = -\log{p}$, we can safely use integers to save weights by e.g. multiplying the weights by 1e6 and truncate to nearest integer. In this way, the truncation error $\Delta w_e = 1$ of integer weights corresponds to relative error $\Delta p /{p}=10^{-6}$ which is small enough. Suppose physical error rate $p$ is in the range of a positive f64 variable (2.2e-308 to 1), the maximum weight is 7e7,which is well below the maximum value of a u32 variable (4.3e9). Since weights only sum up in our algorithm (no multiplication), u32 is large enough and accurate enough. By default we use usize which is platform dependent (usually 64 bits), but you can
We use integer also for ease of migrating to FPGA implementation. In order to fit more vertices into a single FPGA, it's necessary to reduce the resource usage for each vertex. Integers are much cheaper than floating-point numbers, and also it allows flexible trade-off between resource usage and accuracy, e.g. if all weights are equal, we can simply use a 2 bit integer.
Note that other libraries of MWPM solver like Blossom V also default to integer weights as well. Although one can change the macro to use floating-point weights, it's not recommended because "the code may even get stuck due to rounding errors".
Tests
In order to test the correctness of our MWPM solver, we need a ground-truth MWPM solver. Blossom V is widely-used in existing MWPM decoders, but according to the license we cannot embed it in this library.To run the test cases with ground truth comparison or enable the functions like blossom_v_mwpm, you need to download this library at this website to a folder named blossomV at the root directory of this git repo.
wget -c https://pub.ist.ac.at/~vnk/software/blossom5-v2.05.src.tar.gz -O - | tar -xz
cp -r blossom5-v2.05.src/* blossomV/
rm -r blossom5-v2.05.src
Visualization
Visualize the solving procedure of a single decoding problem
To start a server, run the following
cd visualize
python3 server.py # server
# to view it in a browser interactively, you can run the following command to get url
cd ..
cargo test visualize_paper_weighted_union_find_decoder -- --nocapture
# alternatively, you can choose to render locally
npm install # to download packages
node index.js <url> <width> <height> # local render
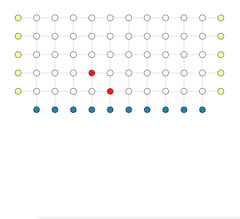
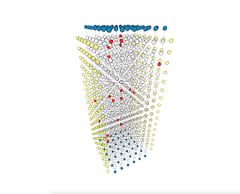
Visualize parallel execution of multiple decoding problems
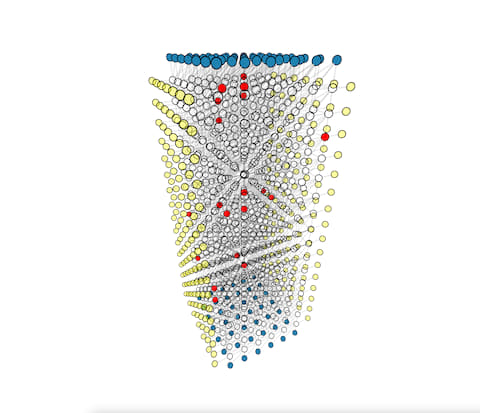
In order to understand the bottleneck of parallel execution, we wrote a visualization tool to display the execution windows of base partitions and fusion operations on multiple threads. Fusion operation only scales with the size of the fusion boundary and the depth of active partitions, irrelevant to the base partition's size. We study different partition and fusion strategies in our paper. Below shows the parallel execution on 64 threads. Blue blocks are base partitions, each consists of 49 rounds of measurement. Green blocks are fusion operations, a single round of measurement sandwiched by two neighbor base partitions. You can click the image which jumps to this interactive visualization tool.
TODOs
- support erasures in parallel solver
Acknowledgements
This project is funded by NSF MRI: Development of PARAGON: Control Instrument for Post NISQ Quantum Computing
References
Fowler, Austin G., et al. "Topological code autotune." Physical Review X 2.4 (2012): 041003.
Criger, Ben, and Imran Ashraf. "Multi-path summation for decoding 2D topological codes." Quantum 2 (2018): 102.
Fowler, Austin G., Adam C. Whiteside, and Lloyd CL Hollenberg. "Towards practical classical processing for the surface code: timing analysis." Physical Review A 86.4 (2012): 042313.
Fowler, Austin G. "Minimum weight perfect matching of fault-tolerant topological quantum error correction in average $ O (1) $ parallel time." arXiv preprint arXiv:1307.1740 (2013).
Higgott, Oscar. "PyMatching: A Python package for decoding quantum codes with minimum-weight perfect matching." ACM Transactions on Quantum Computing 3.3 (2022): 1-16.
Delfosse, Nicolas, and Naomi H. Nickerson. "Almost-linear time decoding algorithm for topological codes." Quantum 5 (2021): 595.
Wu, Yue. APS 2022 March Meeting Talk "Interpretation of Union-Find Decoder on Weighted Graphs and Application to XZZX Surface Code". Slides: https://us.wuyue98.cn/aps2022, Video: https://youtu.be/BbhqUHKPdQk
Higgott, Oscar. PyMatching v2 https://github.com/oscarhiggott/PyMatching
Higgott, Oscar, and Craig Gidney. "Sparse Blossom: correcting a million errors per core second with minimum-weight matching." arXiv preprint arXiv:2303.15933 (2023).
Dependencies
~7–20MB
~285K SLoC