6 releases (3 breaking)
Uses new Rust 2024
| 0.4.0 | May 7, 2025 |
|---|---|
| 0.3.0 | Apr 23, 2025 |
| 0.2.0 | Apr 14, 2025 |
| 0.1.2 | Apr 3, 2025 |
#16 in Simulation
299 downloads per month
220KB
1.5K
SLoC
onq: Operations for Next Generation Quantum Computing
onq is a Rust library for simulating quantum computation and information processing derived strictly from the theoretical first principles.
Unlike conventional quantum computing simulators based on quantum mechanics postulates, onq explores how computational dynamics might emerge necessarily from a single axiom. It aims to model phenomena analogous to quantum computation (superposition, entanglement analogs, interference, stabilization/measurement analogs) without assuming physics, relying instead on the structural and logical consequences defined by the framework provided during its development context.
This library serves as a tool for:
- Exploring the computational implications of the framework.
- Comparing the resulting dynamics with standard quantum mechanics to understand how foundational assumptions shape computation.
- Investigating alternative models of computation derived from abstract principles.
Core Concepts
Key concepts derived and implemented in onq:
- Qualitative Distinction Unit (QDU): (
onq::core::QduId, structonq::core::Qduimplicitly managed by VM/Engine) The fundamental unit, analogous to a qubit. Represents a necessary, bounded distinction with inherent qualitative properties. Interpreted as having a minimal binary basis {Quality0, Quality1}. - Potentiality State: (
onq::core::PotentialityState) Represents the state before stabilization. Uses a complex state vector (Vec<Complex<f64>>) to capture multiple potentialities and phase relationships (inspired bye^(iθ)). For N QDUs, uses a 2N dimensional vector to model integrated states. Assumes initial state|Q0...Q0>. - Operations: (
onq::operations::Operation) Transformations derived from interaction principles (T=P⊗Panalog). Implemented as variants acting on the state vector, including:- Single-QDU
InteractionPatterns with derived matrices (analogs for I, X, Y, Z, H, S, T, S†, T†, √X, √X†, plus φ-based rotations). - General
PhaseShift. ControlledInteraction(using derived conditional gating logic via 4x4 matrix).RelationalLock(using derived non-unitary projection onto Bell states).
- Single-QDU
- ONQ Virtual Machine (ONQ-VM): (
onq::vm::OnqVm) An interpreter that executesPrograms containing sequences ofInstructions. - Program / Instructions: (
onq::vm::Program,onq::vm::Instruction,onq::vm::ProgramBuilder) Defines programs with mixed quantum operations, stabilization, classical memory access (Record), classical computation (arithmetic, logic, compare), and control flow (labels, jumps, branches). - Stabilization: (
onq::vm::Instruction::Stabilize, internalSimulationEngine::stabilize) The analog of measurement. Deterministically resolvesPotentialityStateintoStableState. See "Key Differences" below. - Validation: (
onq::validation::*) Functions to check state normalization and Phase Coherence criteria.
Key Differences from Quantum Mechanics
Understanding onq requires recognizing its fundamental departures from standard quantum mechanics (QM):
- Foundation:
onqderives from abstract logical necessity, not QM postulates derived from physical observation. - "Measurement" (Stabilization): This is the most significant difference.
- QM: Projective measurement is probabilistic (Born rule), collapsing the state vector onto an eigenstate, inherently random for superpositions.
onq:Stabilizeis deterministic. It resolves potentiality based on criteria:- Filtering: Potential outcomes (basis states
|k>) must meet an interpreted Phase Coherence threshold (Score_C1(k) > 0.618) relative to the input state. States failing this cannot be stabilized into. - Scoring: Valid outcomes are weighted by
S(k) = Score_C1(k) * |amplitude_k|^2(interpreting resonance/convergence via amplitude). - Selection: A single outcome
kis chosen deterministically from the valid, scored possibilities using a pseudo-random number generator seeded by a hash of the input state vector. (Same input state -> Same outcome).
- Filtering: Potential outcomes (basis states
- Consequence: Running the same
onqprogram yields the same stabilization results every time. Statistical distributions seen in QM experiments must emerge differently, if at all (perhaps through variations in initial state preparation or environmental interaction, which are not yet modeled).
- Operations: While many operations have QM analogs (H, X, Z, CNOT...), their existence and specific matrix forms are justified solely by interpretation. Unique operations like
PhiRotatemay exist, and standard QM operations might be absent if not derivable. - "Entanglement" (Locking):
RelationalLockuses non-unitary projection to force the state into specific integrated subspaces (Bell states currently), directly modeling Integration/Coherence. This differs from QM where entanglement arises purely from unitary evolution (e.g., CNOT on superposition).
Interpretations, Assumptions, and Limitations
This library is heavily based on interpretation due to the abstract nature and mathematical ambiguities within the source texts provided. Key assumptions include:
- QDU Basis: Assumes a minimal binary {Quality0, Quality1} basis per QDU.
- Initial State: Assumes a default
|Q0...Q0>state. - State Vector Model: Uses a standard complex state vector and interprets operations as matrix multiplications (interpreting
T=P⊗P). - Stabilization Scoring: The metrics used for C1 (neighbour phase diff avg cosine) and C3 (via amplitude
|c_k|^2weighting) are interpretations. The application of the C1>0.618threshold as a filter on outcomes is also an interpretation. - Control Logic:
ControlledInteractionassumes simple gating based on control quality. - Locking:
RelationalLockassumes non-unitary projection is a valid mechanism for achieving integrated states. - Mathematical Gaps: The library cannot fully resolve ambiguities stemming from undefined operators (
⊗,×,∇², etc.) and terms (φ, ψ inΩ(x)).
Therefore, simulation results reflect the behavior of this specific interpretation of the framework.
Current Status
- Core simulation engine for state vector evolution based on derived operations.
- ONQ-VM interpreter supporting mixed quantum/classical programs with control flow.
- stabilization mechanism implemented.
- State validation checks integrated.
- Circuit visualization via
Displaytrait. - Basic tests and examples demonstrating functionality.
- Ongoing: Refinement of interpretations, derivation of more operations, addressing framework ambiguities.
Usage Example (Quantum Teleportation Analog)
// From examples/vm_teleportation.rs
use onq::{
CircuitBuilder, Operation, QduId, Simulator, StableState
};
// Helper for QduId creation for brevity in examples
fn qid(id: u64) -> QduId { QduId(id) }
fn main() {
// Define the three QDUs involved
let msg_q = qid(0); // Message QDU (will be prepared in |+>)
let alice_q = qid(1); // Alice's QDU (part of the Bell pair)
let bob_q = qid(2); // Bob's QDU (part of the Bell pair, receives the state)
println!("QDUs defined: msg={}, alice={}, bob={}", msg_q, alice_q, bob_q);
// --- Build Circuit using Quantum Recovery Logic ---
let mut builder = CircuitBuilder::new();
println!("Building Teleportation Circuit...");
// 1. Prepare Message State: Put msg_q in |+> state
builder = builder.add_op(Operation::InteractionPattern {
target: msg_q,
pattern_id: "Superposition".to_string(), // H analog
});
println!(" Step 1: Prepared Message QDU in |+> state (using Superposition).");
// 2. Create Bell Pair between Alice and Bob: |Φ+> = (1/sqrt(2))(|00> + |11>)
builder = builder.add_op(Operation::InteractionPattern { // H on Alice
target: alice_q,
pattern_id: "Superposition".to_string(),
});
builder = builder.add_op(Operation::ControlledInteraction { // CNOT(Alice, Bob)
control: alice_q,
target: bob_q,
pattern_id: "QualityFlip".to_string(), // X analog
});
println!(" Step 2: Created Bell Pair between Alice and Bob.");
// 3. Alice performs Bell Measurement operations (basis change)
builder = builder.add_op(Operation::ControlledInteraction { // CNOT(Message, Alice)
control: msg_q,
target: alice_q,
pattern_id: "QualityFlip".to_string(),
});
builder = builder.add_op(Operation::InteractionPattern { // H on Message
target: msg_q,
pattern_id: "Superposition".to_string(),
});
println!(" Step 3: Applied Bell Measurement basis change gates (CNOT, H).");
// 4. Quantum Recovery Operations (before stabilization)
// These apply corrections based on the state *before* stabilization.
builder = builder.add_op(Operation::ControlledInteraction { // CNOT(Alice, Bob)
control: alice_q,
target: bob_q,
pattern_id: "QualityFlip".to_string(),
});
builder = builder.add_op(Operation::ControlledInteraction { // CZ(Message, Bob) analog
control: msg_q,
target: bob_q,
pattern_id: "PhaseIntroduce".to_string(), // Use derived Z analog pattern
});
println!(" Step 4: Applied Quantum Recovery gates (CNOT, CZ analog).");
// 5. Stabilize Bob's QDU to observe the teleported state
// Optionally stabilize Alice and Message to see their final states too.
builder = builder.add_op(Operation::Stabilize {
targets: vec![msg_q, alice_q, bob_q],
});
println!(" Step 5: Added final stabilization for all QDUs.");
let circuit = builder.build();
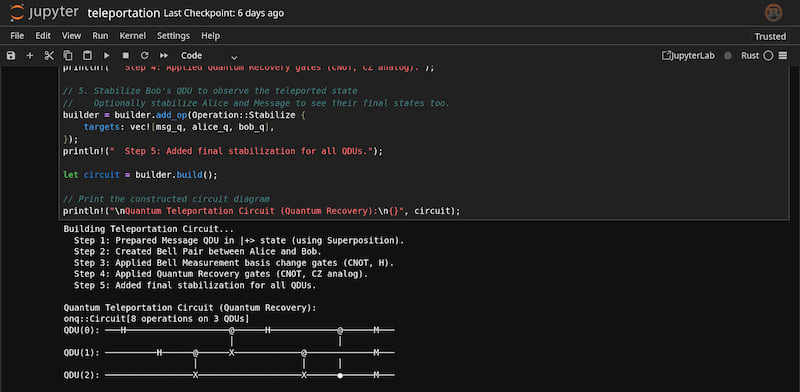
// Print the constructed circuit diagram
println!("\nQuantum Teleportation Circuit (Quantum Recovery):\n{}", circuit);
// --- Run Simulation ---
let simulator = Simulator::new();
println!("\nRunning simulation...");
match simulator.run(&circuit) {
Ok(result) => {
println!("Simulation finished successfully.");
println!("\nSimulation Result Details:");
println!("{}", result);
// --- Basic Result Analysis ---
// Ideally, Bob's QDU (bob_q) now holds the original state of msg_q (which was |+>).
// Stabilizing the |+> state = (1/sqrt(2))[|0> + |1>] depends on the rules.
// Based on our current stabilization (S(0)=0.25, S(1)=0.25), the outcome for Bob
// will be deterministically 0 or 1 based on the final state hash and PRNG.
// A full verification would require state vector tomography (not implemented)
// or running statistical tests if stabilization were probabilistic.
println!("\nAnalysis:");
if let Some(StableState::ResolvedQuality(bob_outcome)) = result.get_stable_state(&bob_q) {
println!("- Bob's QDU ({}) stabilized to state: {}", bob_q, bob_outcome);
println!(" (Note: Expected pre-stabilization state was |+>, outcome {} depends on deterministic stabilization)", bob_outcome);
} else {
println!("- Bob's QDU ({}) was not found in stabilization results.", bob_q);
}
// Print Alice and Message outcomes too
if let Some(StableState::ResolvedQuality(alice_outcome)) = result.get_stable_state(&alice_q) {
println!("- Alice's QDU ({}) stabilized to state: {}", alice_q, alice_outcome);
}
if let Some(StableState::ResolvedQuality(msg_outcome)) = result.get_stable_state(&msg_q) {
println!("- Message's QDU ({}) stabilized to state: {}", msg_q, msg_outcome);
println!(" (These represent the classical bits Alice would send in standard protocol)");
}
println!("\nVerification of perfect state teleportation would require state vector analysis.");
}
Err(e) => {
eprintln!("\n--- Simulation Failed ---");
eprintln!("Error: {}", e);
}
}
}
Development
# Clone the repository (if applicable)
# git clone ...
# cd onq
# Build
cargo build [--release]
# Run tests (unit, integration, doc)
cargo test [--release]
# Run examples
cargo run --example sqrt_flip_demo [--release]
cargo run --example vm_teleportation [--release]
Notebooks
- install jupyter-lab
- install evcxr
- see the
onq/notebooksdirectory
License
Licensed under
MIT license (LICENSE-MIT or http://opensource.org/licenses/MIT)
Contributing
Contributions are welcome! Please feel free to submit issues or pull requests.
Dependencies
~665KB
~12K SLoC