34 releases (19 breaking)
| 0.20.0 | Oct 4, 2024 |
|---|---|
| 0.18.2 | Jul 6, 2024 |
| 0.17.0 | Mar 30, 2024 |
| 0.16.0 | Dec 29, 2023 |
| 0.5.1 | Mar 29, 2022 |
#32 in Audio
1,167 downloads per month
Used in 12 crates
(8 directly)
1MB
20K
SLoC
FunDSP
Audio Processing and Synthesis Library for Rust
FunDSP is an audio DSP (digital signal processing) library for audio processing and synthesis.
FunDSP features a powerful inline graph notation for describing audio processing networks. The notation taps into composable, zero-cost abstractions that express the structure of audio networks as Rust types.
Another innovative feature of FunDSP is its signal flow system, which can determine analytic frequency responses for any linear network.
FunDSP comes with a combinator environment containing a suite of audio components, math and utility functions and procedural generation tools.
Uses
- Audio processing and synthesis for games and applications
- Education
- Music making
- Sound hacking and audio golfing
- Prototyping of DSP algorithms
Rust Audio Discord
To discuss FunDSP and other topics, come hang out with us at the Rust Audio Discord.
Related Projects
bevy_fundsp integrates FunDSP into the Bevy game engine.
midi_fundsp enables the easy creation of live synthesizer software using FunDSP for synthesis.
quartz is a visual programming and DSP playground with releases for Linux, Mac and Windows.
Installation
Add fundsp to your Cargo.toml as a dependency.
[dependencies]
fundsp = "0.19.1"
The files feature is enabled by default. It adds support for
loading of audio files into Wave objects
via the Symphonia crate.
no_std Support
FunDSP supports no_std environments. To enable no_std, disable
the feature std, which is enabled by default. The alloc crate
is still needed for components that allocate memory.
Audio file reading and writing is not available in no_std.
[dependencies]
fundsp = { version = "0.19.1", default-features = false }
Graph Notation
FunDSP Composable Graph Notation expresses audio networks in algebraic form, using graph operators. It was developed together with the functional environment to minimize the number of typed characters needed to accomplish common audio tasks.
Many common algorithms can be expressed in a natural form
conducive to understanding.
For example, an FM oscillator
can be written simply (for some f and m) as:
sine_hz(f) * f * m + f >> sine()
The above expression defines an audio graph that is compiled into a stack allocated, inlined form using the powerful generic abstractions built into Rust. Connectivity errors are detected during compilation, saving development time.
Audio DSP Becomes a First-Class Citizen
With no macros needed, the FunDSP graph notation integrates audio DSP tightly into the Rust programming language as a first-class citizen. Native Rust operator precedences work in harmony with the notation, minimizing the number of parentheses needed.
FunDSP graph expressions offer even more economy in being generic over channel arities, which are encoded at the type level. A mono network can be expressed as a stereo network simply by replacing its mono generators and filters with stereo ones, the graph notation remaining the same.
Basics
Component Systems
There are two parallel component systems: the static AudioNode and the dynamic AudioUnit.
| Trait | Dispatch | Allocation Strategy | Connectivity |
|---|---|---|---|
AudioNode |
static, inlined | stack | input and output arity fixed at compile time |
AudioUnit |
dynamic, object safe | heap | input and output arity fixed after construction |
All AudioNode and AudioUnit components use 32-bit floating point samples (f32).
The main property of a component in either system is that it is a processing node in a graph with a specific number of input and output connections, called its arity. Audio and control signals flow through input and output connections.
Both systems operate on signals synchronously as an infinite stream. The stream can be
rewound to the start at any time using the reset method.
AudioNodes can be stack allocated for the most part.
Some nodes may use the heap for audio buffers and the like.
The allocate method preallocates all needed memory. It should be called last before
sending something into a real-time context. This is done automatically in
the Net and Sequencer frontends.
The purpose of the AudioUnit system is to grant more flexibility in dynamic situations:
decisions about input and output arities and contents can be deferred to runtime.
Conversions
AudioNodes are converted to the AudioUnit system
using the wrapper type An, which implements AudioUnit.
Opcodes in the preludes return nodes already wrapped.
AudioUnits can in turn be converted to AudioNode with the wrapper unit.
In this case, the input and output arities must be provided as type-level constants
U0, U1, ..., for example:
use fundsp::hacker32::*;
// The number of inputs is zero and the number of outputs is one.
let type_erased: An<Unit<U0, U1>> = unit::<U0, U1>(Box::new(white() >> lowpass_hz(5000.0, 1.0) >> highpass_hz(1000.0, 1.0)));
Processing
Processing samples is easy in both AudioNode and AudioUnit systems.
The tick method is for processing single
sample frames, while the process method processes whole blocks.
If maximum speed is important, then it is a good idea to use block processing, as it reduces function calling, processing setup and dynamic network overhead, and enables explicit SIMD support.
Mono samples can be retrieved with get_mono and filter_mono methods. The get_mono method
returns the next sample from a generator that has no inputs and one or two outputs,
while the filter_mono method filters the next sample from
a node that has one input and one output:
let out_sample = node.get_mono();
let out_sample = node.filter_mono(sample);
Stereo samples can be retrieved with get_stereo and filter_stereo methods.
The get_stereo method returns the next stereo sample pair from a generator that
has no inputs and one or two outputs,
while the filter_stereo method filters the next sample
from a node that has two inputs and two outputs.
let (out_left_sample, out_right_sample) = node.get_stereo();
let (out_left_sample, out_right_sample) = node.filter_stereo(left_sample, right_sample);
Block Processing
The buffer module contains buffers for block processing.
The buffers contain 32-bit float samples. There are two types of owned
buffers: the static BufferArray and the dynamic BufferVec.
Buffers are always 64 samples long (MAX_BUFFER_SIZE),
have an arbitrary number of channels, and are explicitly
SIMD
accelerated with the type f32x8 from the wide crate.
The samples are laid out noninterleaved in a flat array.
BufferArray is an audio buffer backed by an array.
The number of channels is a generic parameter which must be known at compile time.
Using this buffer type it is possible to do block processing without allocating heap memory.
BufferVec is an audio buffer backed by a dynamic vector. The buffer is heap allocated.
The number of channels can be decided at runtime.
use fundsp::hacker::*;
// Create a stereo buffer on the stack.
let mut buffer = BufferArray::<U2>::new();
// Declare stereo noise.
let mut node = noise() | noise();
// Process 50 samples into the buffer. There are no inputs, so we can borrow an empty buffer.
node.process(50, &BufferRef::empty(), &mut buffer.buffer_mut());
// Create another stereo buffer, this one on the heap.
let mut filtered = BufferVec::new(2);
// Declare stereo filter.
let mut filter = lowpole_hz(3000.0) | lowpole_hz(3000.0);
// Filter the 50 noise samples.
filter.process(50, &buffer.buffer_ref(), &mut filtered.buffer_mut());
To call process automatically behind the scenes, use the BlockRateAdapter adapter component.
However, it works only with generators, which are components with no inputs.
To access f32 values in a buffer, use methods with the f32 suffix, for example,
at_f32 or channel_f32.
Sample Rate Independence
Of the signals flowing in graphs, some contain audio while others are controls of different kinds.
With control signals and parameters in general, we prefer to use natural units like Hz and seconds. It is useful to keep parameters independent of the sample rate, which we can then adjust as we like.
In addition to sample rate adjustments, natural units enable support for
selective oversampling (with the oversample component)
in nested sections that are easy to configure and modify.
Some low-level components ignore the sample rate by design, such as the single sample delay tick.
The default sample rate is 44.1 kHz.
In both systems, the sample rate can be set for component A, and any children it may have,
via A.set_sample_rate(sample_rate).
Audio Processing Environment
FunDSP preludes define convenient combinator environments for audio processing.
There are three name-level compatible versions of the prelude.
The default environment (fundsp::prelude) offers a generic interface.
The 64-bit hacker environment (fundsp::hacker) for audio hacking
uses 64-bit internal state for components to maximize audio quality.
The 32-bit hacker environment (fundsp::hacker32) uses 32-bit internal
state for components. It aims to offer maximum processing speed.
An application interfacing fundsp can mix and match preludes as needed.
The aims of the environments are:
- Minimize the number of characters needed to type to express an idiom.
- Keep the syntax clean so that a subset of the hacker environment can be parsed straightforwardly as a high-level DSL for quick prototyping.
- Make the syntax usable even to people with no prior exposure to programming.
Deterministic Pseudorandom Phase
FunDSP uses a deterministic pseudorandom phase system for audio generators. Generator phases are seeded from network structure and node location.
Thus, two identical networks sound identical separately but different when combined.
This means that noise() | noise() is a stereo noise source, for example.
Pseudorandom phase is an attempt to decorrelate different channels of audio. It is also used to pick sample points for envelopes, contributing to a "warmer" sound.
Operators
Custom operators are available for combining audio components inline. In order of precedence, from highest to lowest:
| Expression | Meaning | Inputs | Outputs | Notes |
|---|---|---|---|---|
-A |
negate A |
a |
a |
Negates any number of outputs, even zero. |
!A |
thru A |
a |
same as inputs | Passes through extra inputs. |
A * B |
multiply A with B |
a + b |
a = b |
Aka amplification, or ring modulation when both are audio signals. Number of outputs in A and B must match. |
A * constant |
multiply A |
a |
a |
Broadcasts constant. Same applies to constant * A. |
A + B |
sum A and B |
a + b |
a = b |
Aka mixing. Number of outputs in A and B must match. |
A + constant |
add to A |
a |
a |
Broadcasts constant. Same applies to constant + A. |
A - B |
difference of A and B |
a + b |
a = b |
Number of outputs in A and B must match. |
A - constant |
subtract from A |
a |
a |
Broadcasts constant. Same applies to constant - A. |
A >> B |
pipe A to B |
a |
b |
Aka chaining. Number of outputs in A must match number of inputs in B. |
A & B |
bus A and B |
a = b |
a = b |
Sum A and B. A and B must have identical connectivity. |
A ^ B |
branch input to A and B in parallel |
a = b |
a + b |
Number of inputs in A and B must match. |
A | B |
stack A and B in parallel |
a + b |
a + b |
Concatenates A and B inputs and outputs. |
In the table, constant denotes an f32 value.
All operators are associative, except the left associative -.
An alternative to some operators are functions available in the preludes. Some of them have multiple combination versions; these work only for multiples of the same type of node, with statically (at compile time) set number of nodes.
The nodes are allocated inline in all functions, as are any inner buffers needed for block processing.
| Operator Form | Function Form | Multiple Combination Forms |
|---|---|---|
!A |
thru(A) |
- |
A * B |
product(A, B) |
- |
A + B |
sum(A, B) |
sumi, sumf |
A >> B |
pipe(A, B) |
pipei, pipef |
A & B |
bus(A, B) |
busi, busf |
A ^ B |
branch(A, B) |
branchi, branchf |
A | B |
stack(A, B) |
stacki, stackf |
Operators Diagram
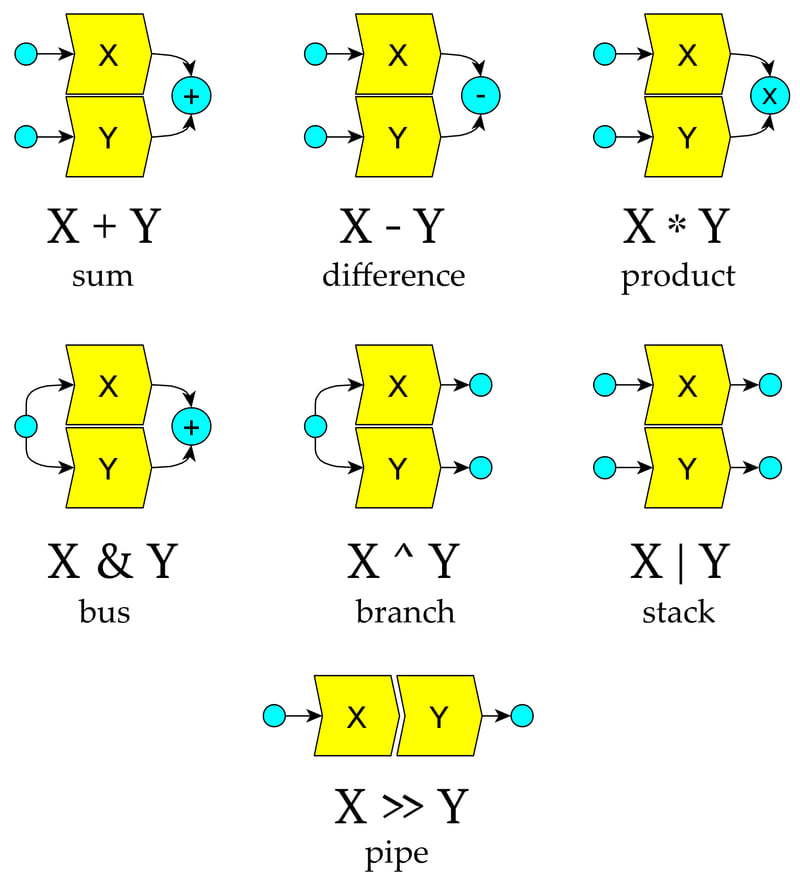
Each cyan dot in the diagram above can contain an arbitrary number of channels, including zero.
In the AudioNode system the number of channels is determined statically, at compile time,
while in the AudioUnit system (using Net) the number of channels can be
decided at runtime.
Broadcasting
Arithmetic operators are applied to outputs channelwise.
Arithmetic between two components never broadcasts channels: channel arities have to match always.
Direct arithmetic with f32 values, however, broadcasts to an arbitrary number of channels.
The negation operator broadcasts also: -A is equivalent with (0.0 - A).
For example, A * constant(2.0) and A >> mul(2.0) are equivalent and expect A to have one output.
On the other hand, A * 2.0 works with any A, even with zero outputs.
Thru
The thru (!) operator is syntactic sugar for chaining filters with similar connectivity.
It adjusts output arity to match input arity and passes through any missing outputs to the next node. The missing outputs are parameters to the filter.
For example, while lowpass() is a 2nd order lowpass filter, !lowpass() >> lowpass()
is a steeper 4th order lowpass filter with identical connectivity.
The thru operator is also available as a function: thru(A) is equivalent with !A.
Generators, Filters and Sinks
Components can be broadly classified into generators, filters and sinks. Generators have only outputs, while filters have both inputs and outputs.
Sinks are components with no outputs. Direct arithmetic on a sink translates to a no-op.
In the prelude, sink() returns a mono sink.
Graph Combinators
Of special interest among operators are the four custom combinators:
pipe ( >> ), bus ( & ), branch ( ^ ), and stack ( | ).
The pipe is a serial operator where components appear in processing order. Branch, stack, and arithmetic operators are parallel operators where components appear in channel order.
The bus is a commutative operator where components may appear in any order. The other operators are not commutative in general.
All four are fully associative, and each come with their own connectivity rules.
Pipe
The pipe ( >> ) operator builds traditional processing chains akin to composition of functions.
A runs first, then B. In A >> B, each output of A is piped to a matching input of B, so
the output arity of A must match the input arity of B.
The whole combination then has the input arity of A and the output arity of B.
Pipe is a fundamental operation. It wires units in series.
The pipe operation is also available as a function: pipe(A, B) is equal to A >> B.
Branch
Where the arithmetic operators are reducing in nature,
the branch ( ^ ) operator splits a signal into parallel branches.
In A ^ B, both components receive the same input but their outputs are disjoint.
Because the components receive the same input, the number of inputs in A and B must match.
In A ^ B, the outputs of A appear first, followed with outputs of B.
Branching is useful for building banks of components such as filters.
The branch operation is also available as a function: branch(A, B) is equal to A ^ B.
Bus
The bus ( & ) operator can be thought of as an inline audio bus
with a fixed set of input and output channels.
It builds signal buses from components with identical connectivity.
In A & B, the same input is sent to both A and B, and their outputs are mixed together.
Components in a bus may appear in any order.
The bus is especially useful because it does not alter connectivity: we can always bus together any set of matching components without touching the rest of the expression.
Both A + B and A & B are mixing operators. The difference between the two is that A + B is reducing:
A and B have their own, disjoint inputs, which are combined at the output.
In A & B, both components source from the same inputs, and the number of inputs must match.
One application of the bus is controlling effect mix in conjunction with the pass opcode,
which passes signal through unchanged. For example, to add 20% chorus to a mono signal,
one might type pass() & 0.2 * chorus(0, 0.0, 0.01, 0.3).
Or, to add 20% reverb to a stereo signal, multipass() & 0.2 * reverb_stereo(20.0, 2.0, 1.0).
Type inference works in our favor here, saving us the need to write the arity of multipass,
and the constant 0.2 is broadcast to two channels.
The bus operation is also available as a function: bus(A, B) is equal to A & B.
Stack
The stack ( | ) operator builds composite components.
It can be applied to any two components.
As a graph operator, the stack corresponds to the disjoint union.
In A | B, the inputs and outputs of A and B
are disjoint and they are processed independently, in parallel.
In stacks, components are written in channel order.
In A | B | C, channels of A come first, followed by channels of B, then C.
The stack is often used to build filter parameters. For example, in
(pass() | constant((440.0, 1.0))) >> lowpass() the input signal is passed through
the stack and two other signals, frequency and Q, are concatenated to it to form the input
to a lowpass filter.
The stack operation is also available as a function: stack(A, B) is equal to A | B.
Expressions Are Graphs
The expression A >> (B ^ C ^ D) defines a signal processing graph.
It has whatever inputs A has, and outputs everything from B and C and D in parallel.
The whole structure is packed, monomorphized and inlined with the constituent nodes consumed. If you want to reuse components, define them as functions or closures, or clone them. See the preludes for examples.
Connectivity is checked during compilation.
Mismatched connectivity will result in a compilation error complaining about mismatched
typenum types.
The arrays Frame<f32, Size> that connect components in tick come from the
generic-array and
numeric-array crates.
Computational Structure
Graph combinators consume their arguments. This prevents cycles and imposes an overall tree shape on the resulting computation graph.
Implicit cycle prevention means that the built structures are always computationally efficient in the dataflow sense. All reuse of computed data takes place locally, inside combinators and components.
There are two main ways to structure the reuse of signals in FunDSP graph notation: branching and busing. Both are exposed as fundamental operators, guiding toward efficient structuring of computation. Dataflow concerns are thus explicated in the graph notation itself.
Net
The graph notation can get cumbersome for complex graphs. Also, sometimes the number of inputs and outputs is not known until runtime.
The Net component offers an explicit graph interface
for connecting AudioUnit nodes.
Arity of the net is specified as constructor arguments.
For example, to build dc(220.0) >> sine() dynamically using Net:
use fundsp::hacker::*;
// Instantiate network with 0 inputs and 1 output.
let mut net = Net::new(0, 1);
// Add nodes, obtaining their IDs.
let dc_id = net.push(Box::new(dc(220.0)));
let sine_id = net.push(Box::new(sine()));
// Connect nodes.
net.pipe_all(dc_id, sine_id);
net.pipe_output(sine_id);
The overhead of Net is the overhead of calling into Box<dyn AudioUnit>
objects. Beyond that, the dynamic versions are roughly as efficient
as the static ones.
The graph syntax is also available for combining Net instances.
Connectivity checks are then deferred to runtime.
Networks can also be combined inline with components from the preludes.
The components are first converted to Net.
When we need dynamic processing, we can start it with Net::wrap,
which converts any unit into a network. Also, we can control when
to cross from the static realm into the dynamic by the placement of Net::wrap.
use fundsp::hacker::*;
// Wrap saw wave in a network.
let mut net = Net::wrap(Box::new(saw()));
// Now we can add filters conditionally.
let add_filter = true;
if add_filter {
net = net >> lowpass_hz(1000.0, 1.0);
}
For real-time situations, a Net can be divided into a frontend
and a backend. The frontend handles changes to the network,
while the real-time safe backend renders audio.
use fundsp::hacker::*;
let mut net = Net::new(0, 1);
let noise_id = net.chain(Box::new(pink()));
// Create the backend.
let mut backend = net.backend();
// The backend is now ready to be sent into an audio thread.
// We can make changes to the frontend and then commit them to the backend.
net.replace(noise_id, Box::new(brown()));
net.commit();
// We can also use the graph syntax to make changes, as long as connectivity
// is maintained at commit time.
net = net >> peak_hz(1000.0, 1.0);
net.commit();
/// Nodes can be replaced smoothly with a crossfade to avoid clicks.
net.crossfade(noise_id, Fade::Smooth, 1.0, Box::new(white()));
net.commit();
Using dynamic networks incurs some overhead so it is an especially good idea to use block processing, which neutralizes it effectively.
Sequencer
The Sequencer component mixes together generator nodes dynamically.
It can start and stop rendering nodes with sample accuracy.
The sequencer has no inputs and a user specified number of outputs.
use fundsp::hacker::*;
// Create stereo sequencer.
// The first argument should be set true if we want to replay events after `reset`.
let mut sequencer = Sequencer::new(false, 2);
Adding new events, their start and stop times as well as fade-in and fade-out envelopes
can be set. The sequencer returns an ID that can be used for later edits to the events.
// Add a new event with start time 1.0 seconds and end time 2.0 seconds.
// Fade-in time is 0.1 seconds, while the fade-out time is 0.2 seconds.
// This returns an `EventId`.
let id1 = sequencer.push(1.0, 2.0, Fade::Smooth, 0.1, 0.2, Box::new(noise() | noise()));
// Add a new event that starts immediately and plays indefinitely.
let id2 = sequencer.push_relative(0.0, f64::INFINITY, Fade::Smooth, 0.1, 0.2, Box::new(pink() | pink()));
For use as a dynamic mixer, the sequencer can be split into a frontend and a backend. The frontend is for adding and editing events, and the real-time safe backend renders audio.
// Get a backend for this sequencer. This sequencer is then the frontend.
let mut backend = sequencer.backend();
// Now we can insert the backend into, for example, a `Net`.
// Later we can use the frontend to create events and make edits to them; the end time and fade-out time
// can be changed. Here we start fading out the event immediately with an envelope duration of 0.1 seconds.
sequencer.edit_relative(id2, 0.0, 0.1);
Input Modalities And Ranges
Some signals found flowing in audio networks.
| Modality | Preferred Units/Range | Notes |
|---|---|---|
| frequency | Hz | |
| phase | 0...1 | The wavetable oscillator uses this range. |
| time | s | |
| audio data | -1...1 | Inner processing may use any range that is convenient. However, only special output formats can store audio data outside this range. |
| stereo pan | -1...1 (left to right) | For ergonomy, consider clamping any pan input to this range. |
| control amount | 0...1 | If there is no natural interpretation of the parameter. |
Working With Waves
FunDSP includes a multichannel wave abstraction called Wave.
For example, to render 10 seconds of pink noise:
use fundsp::hacker::*;
let wave1 = Wave::render(44100.0, 10.0, &mut (pink()));
Then filter it with a moving bandpass filter and normalize samples to -1..1:
let mut wave2 = wave1.filter(10.0, &mut ((pass() | lfo(|t| (xerp11(110.0, 880.0, spline_noise(0, t * 5.0)), 1.0))) >> bandpass()));
wave2.normalize();
Saving of waves is possible in 16-bit or 32-bit WAV
when the std feature is enabled.
The 16-bit format is integer based while the 32-bit format is floating point.
For example, to save wave2 to test.wav:
wave2.save_wav16("test.wav").expect("Could not save wave.");
Loading of audio files in various formats is handled by the
Symphonia crate.
Symphonia integration is enabled by the files feature, which is enabled by default.
The std feature must be enabled also.
For example, to load test.wav:
let wave3 = Wave::load("test.wav").expect("Could not load wave.");
Individual channels of waves can be played back with the wavech and wavech_at opcodes.
Signal Flow Analysis
FunDSP features a comprehensive signal flow system that analyzes causal latencies and frequency responses in audio networks.
The system can calculate the frequency response of any linear network analytically by composing transfer functions and folding constants. Linear networks are constructed from linear filters, delays, and the operations of:
- Mixing.
- Chaining. Chaining of linear filters and delays maintains linearity.
- Constant scaling. Signals may be scaled by constant factors.
Signal latencies are similarly analyzed from input to output in detail, facilitating automatic removal of pre-delay from effects chains. The definition of latency is one of involuntary causal kind, so voluntarily placed delay elements do not count as latency.
For example,
FIR filters
can be composed inline from single sample delays (the tick opcode) and arithmetic.
Signal flow analysis will readily reveal that a 2-point averaging filter
has zero gain at the Nyquist frequency,
while a 3-point averaging filter does not:
use fundsp::hacker::*;
assert!((pass() & tick()).response(0, 22050.0).unwrap().norm() < 1.0e-9);
assert!((pass() & tick() & tick() >> tick()).response(0, 22050.0).unwrap().norm() > 0.1);
However, with appropriate scaling a 3-point FIR can vanish, too:
use fundsp::hacker::*;
assert!((0.5 * pass() & tick() & 0.5 * tick() >> tick()).response(0, 22050.0).unwrap().norm() < 1.0e-9);
Filters
List of Linear Filters
Verified frequency responses are available for all linear filters.
| Opcode | Type | Parameters | Family | Notes |
|---|---|---|---|---|
allpass |
allpass (2nd order) | frequency, Q | Simper SVF | |
allpole |
allpass (1st order) | delay | 1st order | Adjustable delay at DC in samples. |
bandpass |
bandpass (2nd order) | frequency, Q | Simper SVF | |
bell |
peaking (2nd order) | frequency, Q, gain | Simper SVF | Adjustable amplitude gain. |
biquad |
biquad (2nd order) | - | biquad | Arbitrary biquad with fixed parameters. |
butterpass |
lowpass (2nd order) | frequency | biquad | Butterworth lowpass has a maximally flat passband and monotonic frequency response. |
dcblock |
DC blocker (1st order) | frequency | 1st order | Zero centers signal, countering any constant offset ("direct current"). |
fir |
FIR | - | FIR | |
follow |
lowpass (3rd order) | response time | nested 1st order | Smoothing filter with adjustable edge response time. |
highpass |
highpass (2nd order) | frequency, Q | Simper SVF | |
highpole |
highpass (1st order) | frequency | 1st order | |
highshelf |
high shelf (2nd order) | frequency, Q, gain | Simper SVF | Adjustable amplitude gain. |
lowpass |
lowpass (2nd order) | frequency, Q | Simper SVF | |
lowpole |
lowpass (1st order) | frequency | 1st order | |
lowshelf |
low shelf (2nd order) | frequency, Q, gain | Simper SVF | Adjustable amplitude gain. |
morph |
morphing (2nd order) | frequency, Q, morph | Simper SVF | Morphs between lowpass, peaking and highpass modes. |
notch |
notch (2nd order) | frequency, Q | Simper SVF | |
peak |
peaking (2nd order) | frequency, Q | Simper SVF | |
pinkpass |
lowpass (3 dB/octave) | - | mixed FIR / 1st order | Turns white noise into pink noise. |
resonator |
bandpass (2nd order) | frequency, Q | biquad | Gain stays constant as Q is varied. |
Parameter Smoothing Filter
The follow filter is special. It supports different rates for rising (attack) and falling (release) segments.
For example, afollow(0.1, 0.2) has a 0.1 second attack and a 0.2 second release.
It also jumps immediately to the very first value in the input stream, and starts smoothing from there. This means the output value is always within input bounds.
List of Nonlinear Filters
Unlike linear filters, nonlinear filters are sensitive to incoming signal level. Due to nonlinearity, we do not attempt to calculate frequency responses for these filters.
| Opcode | Type | Parameters | Family | Notes |
|---|---|---|---|---|
bandrez |
bandpass (2nd order) | frequency, Q | nested 1st order | |
dbell |
peaking (2nd order) | frequency, Q, gain | dirty biquad | Biquad with nonlinear state shaping and adjustable amplitude gain. |
dhighpass |
highpass (2nd order) | frequency, Q | dirty biquad | |
dlowpass |
lowpass (2nd order) | frequency, Q | dirty biquad | |
dresonator |
bandpass (2nd order) | frequency, Q | dirty biquad | |
fbell |
peaking (2nd order) | frequency, Q, gain | feedback biquad | Biquad with nonlinear feedback and adjustable amplitude gain. |
fhighpass |
highpass (2nd order) | frequency, Q | feedback biquad | |
flowpass |
lowpass (2nd order) | frequency, Q | feedback biquad | |
fresonator |
bandpass (2nd order) | frequency, Q | feedback biquad | |
lowrez |
lowpass (2nd order) | frequency, Q | nested 1st order | |
moog |
lowpass (4th order) | frequency, Q | Moog ladder |
Frequency Domain Resynthesis
Filtering and other effects can be done in the
frequency domain
as well with the resynth opcode.
The resynthesizer Fourier transforms input windows to the frequency domain with an overlap of four. A processing function then translates these inputs to frequency domain outputs. The output windows are inverse transformed and overlap-added.
The resynthesizer can reconstruct inputs exactly, so an effect can be made to vary smoothly between an input and a processed version.
For example, to implement a highly selective FFT bandpass filter:
use fundsp::hacker32::*;
// The window length, which must be a power of two and at least four,
// determines the frequency resolution. Latency is equal to the window length.
let window_length = 1024;
// Passband in Hz.
let pass_min = 1000.0;
let pass_max = 2000.0;
// The number of input and output channels is user configurable.
// Here both are 1 (`U1`).
let synth = resynth::<U1, U1, _>(window_length, |fft|
for i in 0..fft.bins() {
if fft.frequency(i) >= pass_min && fft.frequency(i) <= pass_max {
fft.set(0, i, fft.at(0, i));
}
});
The processing function can obtain window time from the supplied FFT window object, to support time varying effects.
For more information on the technique, see Fourier analysis and reconstruction of audio signals.
More On Multithreading And Real-Time Control
Besides Net and Sequencer frontends, there are two ways to introduce real-time
control to graph expressions: shared atomic variables and setting listeners.
Atomic Variables
We may use shared atomic variables to communicate data from and to external contexts. A shared variable is declared with an initial value:
use fundsp::hacker::*;
let amp = shared(1.0);
Shared variables can be cloned and sent into another thread.
To instantiate a shared variable output into an audio graph, use var and var_fn opcodes.
For example, to control amplitude:
let amp_controlled = noise() * var(&);
Later we can set the amplitude from anywhere:
amp.set_value(0.5);
A useful pattern is piping a shared variable through a follow filter
to smooth parameter changes, here with a 0.1 second response time:
let amp_controlled = noise() * (var(&) >> follow(0.1));
The timer opcode maintains stream time in a shared variable.
The timer node has no inputs or outputs and can be joined to any node by stacking.
Settings
Settings are all kinds of node parameters with no dedicated inputs.
A node can respond to one or more types of settings, which are
applied using the set method.
use fundsp::hacker::*;
let mut node = afollow(0.1, 1.0);
node.set(Setting::attack_release(0.2, 2.0));
To adjust settings from other threads, a node can be
wrapped inside a setting listener with the listen(node)
opcode. It returns a (sender, node) pair.
The sender can be cloned and invoked from other threads.
The format of settings available through sender depends
on the type of the graph.
Nodes inside structures can be accessed via addressing:
Setting Call |
Address Meaning |
|---|---|
left() |
Pick left side of binary operation. |
right() |
Pick right side of binary operation. |
index(i) |
Pick index i inside structure such as busi. |
node(id) |
Pick node with id inside Net. |
Addresses are specified after the parameter constructor. They can be nested up to four levels deep.
If a listener is attached to a binary operation, then the
different sides can be picked with the left or right method.
For example, constants are exposed as scalar settings:
use fundsp::hacker::*;
let (sender, node) = listen(dc(0.5) >> resample(pink()));
sender.try_send(Setting::value(0.6).left()).expect("Cannot send setting.");
If a parameter has a dedicated input then it cannot be a setting.
The way to get filters with parameters controlled via settings
is to use the forms that specify all parameters
as constant, for example, lowpass_hz.
use fundsp::hacker::*;
let (sender, node) = listen(lowpass_hz(1000.0, 1.0));
Later we can send filter parameters from anywhere via sender.
For example, the lowpass filter supports setting cutoff frequency and Q value.
Set filter cutoff to 2 kHz and Q to 2.0:
sender.try_send(Setting::center_q(2000.0, 2.0)).expect("Cannot send setting.");
The following table summarizes the available settings.
| Opcode | Setting Constructor Call |
|---|---|
afollow |
attack_release to set attack and release times in seconds |
allnest_c |
delay in samples at DC |
allpass_hz |
center_q |
allpole_delay |
delay in samples at DC |
bandpass_hz |
center_q |
bell_hz |
center_q_gain |
biquad |
biquad to set biquad coefficients |
butterpass_hz |
center |
constant |
value to set scalar value on all channels |
dbell_hz |
center_q_gain |
dc |
value to set scalar value on all channels |
dcblock_hz |
center |
dhighpass_hz |
center_q |
dlowpass_hz |
center_q |
dresonator_hz |
center_q |
dsf_saw_r |
roughness in 0...1 |
dsf_square_r |
roughness in 0...1 |
fbell_hz |
center_q_gain |
fhighpass_hz |
center_q |
flowpass_hz |
center_q |
follow |
time to set follow time in seconds |
fresonator_hz |
center_q |
highpass_hz |
center_q |
highpole_hz |
center |
highshelf_hz |
center_q_gain |
hold |
variability in 0...1 |
lowpass_hz |
center_q |
lowpole_hz |
center |
lowshelf_hz |
center_q_gain |
moog_hz |
center_q |
notch_hz |
center_q |
pan |
pan to set pan value in -1...1 |
peak_hz |
center_q |
resonator_hz |
center_q |
If a node responds to center_q_gain, then it also responds to center_q and center.
If a node responds to center_q, then it also responds to center.
Parametric Equalizer Recipe
In this example we make a 12-band, double precision parametric equalizer
using the peaking bell filter.
The sample type, as always, is 32-bit floating point (f32).
First, declare the processing pipeline. Here we space the bands at 1 kHz increments starting from 1 kHz, set Q values to 1.0 and set gains of all bands to 0 dB initially:
use fundsp::hacker::*;
let mut equalizer = pipei::<U12, _, _>(|i| bell_hz(1000.0 + 1000.0 * i as f32, 1.0, db_amp(0.0)));
The type of the equalizer is An<Chain<U12, FixedSvf<f64, BellMode<f64>>>>.
The equalizer is ready to use immediately. Filter samples:
let output_sample = equalizer.filter_mono(input_sample);
We can access individual bands via equalizer.node(i) and equalizer.node_mut(i)
where i ranges from 0 to 11.
Set band 0 to amplify by 10 dB at 500 Hz with Q set to 2.0:
equalizer.node_mut(0).set_gain(db_amp(10.0));
equalizer.node_mut(0).set_center(500.0);
equalizer.node_mut(0).set_q(2.0);
For plotting the frequency response, we can query the equalizer. Query equalizer gain at 1 kHz:
let decibel_gain_at_1k = equalizer.response_db(0, 1000.0).unwrap();
The default sample rate is 44.1 kHz. Set sample rate to 48 kHz:
equalizer.set_sample_rate(48_000.0);
For real-time control, the equalizer can be equipped with a setting listener.
let (sender, equalizer) = listen(equalizer);
Then, we can send settings to change center frequency, Q and gain.
The settings are available because we constructed the filter using
the bell_hz form.
Set band 1 to amplify by 3 dB at 1000 Hz with Q set to 2.0:
sender.try_send(Setting::center_q_gain(1000.0, 2.0, db_amp(3.0)).index(1)).expect("Cannot send setting.");
evcxr
The display method returns information about a node,
including an ASCII chart of the frequency response of channel 0.
Here is an example of using evcxr
to examine frequency responses interactively:
C:\rust>evcxr
Welcome to evcxr. For help, type :help
>> :dep fundsp
>> use fundsp::hacker::*;
>> print!("{}", bell_hz(1000.0, 1.0, db_amp(50.0)).display())
60 dB ------------------------------------------------ 60 dB
50 dB -------------------------.---------------------- 50 dB
*
40 dB -------------------------*---------------------- 40 dB
**
30 dB -----------------------.***--------------------- 30 dB
******.
20 dB -------------------..*********.----------------- 20 dB
..**************.
10 dB -------------..********************..----------- 10 dB
..*****************************...
0 dB ....***************************************..... 0 dB
| | | | | | | | | |
10 50 100 200 500 1k 2k 5k 10k 20k Hz
Peak Magnitude : 50.00 dB (1000 Hz)
Inputs : 1
Outputs : 1
Latency : 0.0 samples
Footprint : 96 bytes
>>
Free Functions
These free functions are available in the environment.
Component Opcodes
The type parameters in the table refer to the hacker preludes.
I, M, N, O, U are type-level integers. They are U0, U1, U2...
| Function | Inputs | Outputs | Explanation |
|---|---|---|---|
add(x) |
x |
x |
Add constant x to signal. |
adsr_live(a, d, s, r) |
1 | 1 | ADSR envelope. Attack time a, decay time d, sustain level s, and release time r. Input > 0.0 starts attack, input <= 0.0 starts release. Output in [0.0, 1.0]. |
afollow(a, r) |
1 | 1 | Asymmetric smoothing filter with halfway attack time a seconds and halfway release time r seconds. |
allnest(x) |
2 (input, coefficient) | 1 | Nested allpass with inner allpass processing x. |
allnest_c(c, x) |
1 | 1 | Nested allpass with feedforward coefficient c and inner allpass processing x. |
allpass() |
3 (audio, frequency, Q) | 1 | Allpass filter (2nd order). |
allpass_hz(f, q) |
1 | 1 | Allpass filter (2nd order) centered at f Hz with Q q. |
allpass_q(q) |
2 (audio, frequency) | 1 | Allpass filter (2nd order) with Q q. |
allpole() |
2 (audio, delay) | 1 | Allpass filter (1st order). 2nd input is delay in samples (delay > 0). |
allpole_delay(delay) |
1 | 1 | Allpass filter (1st order) with delay at DC in samples (delay > 0). |
bandpass() |
3 (audio, frequency, Q) | 1 | Bandpass filter (2nd order). |
bandpass_hz(f, q) |
1 | 1 | Bandpass filter (2nd order) centered at f Hz with Q q. |
bandpass_q(q) |
2 (audio, frequency) | 1 | Bandpass filter (2nd order) with Q q. |
bandrez() |
3 (audio, frequency, Q) | 1 | Resonant bandpass filter (2nd order). |
bandrez_hz(f, q) |
1 | 1 | Resonant bandpass filter (2nd order) centered at f Hz with resonance q in 0...1. |
bandrez_q(q) |
2 (audio, frequency) | 1 | Resonant bandpass filter (2nd order) with resonance q in 0...1. |
bell() |
4 (audio, frequency, Q, gain) | 1 | Peaking filter (2nd order) with adjustable amplitude gain. |
bell_hz(f, q, gain) |
1 | 1 | Peaking filter (2nd order) centered at f Hz with Q q and amplitude gain gain. |
bell_q(q, gain) |
2 (audio, frequency) | 1 | Peaking filter (2nd order) with Q q and amplitude gain gain. |
biquad(a1, a2, b0, b1, b2) |
1 | 1 | Arbitrary biquad filter with coefficients in normalized form. |
brown() |
- | 1 | Brown noise. |
branch(x, y) |
x = y |
x + y |
Branch into x and y. Identical with x ^ y. |
branchi::<U, _, _>(f) |
f |
U * f |
Branch into U nodes from indexed generator f. |
branchf::<U, _, _>(f) |
f |
U * f |
Branch into U nodes from fractional generator f, e.g., | x | resonator_hz(xerp(20.0, 20_000.0, x), xerp(5.0, 5_000.0, x)). |
bus(x, y) |
x = y |
x = y |
Bus x and y. Identical with x & y. |
busi::<U, _, _>(f) |
f |
f |
Bus together U nodes from indexed generator f, e.g., | i | mul(i as f32 + 1.0) >> sine(). |
busf::<U, _, _>(f) |
f |
f |
Bus together U nodes from fractional generator f. |
butterpass() |
2 (audio, frequency) | 1 | Butterworth lowpass filter (2nd order). |
butterpass_hz(f) |
1 | 1 | Butterworth lowpass filter (2nd order) with cutoff frequency f Hz. |
chorus(seed, sep, var, mod) |
1 | 1 | Chorus effect with LFO seed seed, voice separation sep seconds, delay variation var seconds and LFO modulation frequency mod Hz. |
clip() |
1 | 1 | Clip signal to -1...1. |
clip_to(min, max) |
1 | 1 | Clip signal to min...max. |
constant(x) |
- | x |
Constant signal x. Synonymous with dc. |
dbell(shape) |
4 (audio, frequency, Q, gain) | 1 | Dirty biquad bell equalizer (2nd order) with feedback shape, for example, Tanh(1.0). |
dbell_hz(shape, f, q, gain) |
1 | 1 | Dirty biquad bell equalizer (2nd order) with feedback shape, center f Hz, Q value q and amplitude gain gain. |
dc(x) |
- | x |
Constant signal x. Synonymous with constant. |
dcblock() |
1 | 1 | Zero center signal with cutoff frequency 10 Hz. |
dcblock_hz(f) |
1 | 1 | Zero center signal with cutoff frequency f. |
declick() |
1 | 1 | Apply 10 ms of fade-in to signal. |
declick_s(t) |
1 | 1 | Apply t seconds of fade-in to signal. |
delay(t) |
1 | 1 | Delay of t seconds. Delay time is rounded to the nearest sample. |
dhighpass(shape) |
3 (audio, frequency, Q) | 1 | Dirty biquad highpass (2nd order) with feedback shape, for example, Tanh(1.0). |
dhighpass_hz(shape, f, q) |
1 | 1 | Dirty biquad highpass (2nd order) with feedback shape, center f Hz and Q q. |
dlowpass(shape) |
3 (audio, frequency, Q) | 1 | Dirty biquad lowpass (2nd order) with feedback shape, for example, Tanh(1.0). |
dlowpass_hz(shape, f, q) |
1 | 1 | Dirty biquad lowpass (2nd order) with feedback shape, center f Hz and Q q. |
dresonator(shape) |
3 (audio, frequency, Q) | 1 | Dirty biquad resonator (2nd order) with feedback shape, for example, Tanh(1.0). |
dresonator_hz(shape, f, q) |
1 | 1 | Dirty biquad resonator (2nd order) with feedback shape, center f Hz and Q q. |
dsf_saw() |
2 (frequency, roughness) | 1 | Saw-like discrete summation formula oscillator. |
dsf_saw_r(r) |
1 (frequency) | 1 | Saw-like discrete summation formula oscillator with roughness r in 0...1. |
dsf_square() |
2 (frequency, roughness) | 1 | Square-like discrete summation formula oscillator. |
dsf_square_r(r) |
1 (frequency) | 1 | Square-like discrete summation formula oscillator with roughness r in 0...1. |
envelope(f) |
- | f |
Time-varying control f with scalar or tuple output, e.g., |t| exp(-t). Synonymous with lfo. |
envelope2(f) |
1 (x) | f |
Time-varying, input dependent control f with scalar or tuple output, e.g., |t, x| exp(-t * x). Synonymous with lfo2. |
envelope3(f) |
2 (x, y) | f |
Time-varying, input dependent control f with scalar or tuple output, e.g., |t, x, y| y * exp(-t * x). Synonymous with lfo3. |
envelope_in(f) |
f |
f |
Time-varying, input dependent control f with scalar or tuple output, e.g., |t, i: &Frame<f32, U1>| exp(-t * i[0]). Synonymous with lfo_in. |
fbell(shape) |
4 (audio, frequency, Q, gain) | 1 | Feedback biquad bell equalizer (2nd order) with feedback shape, for example, Tanh(1.0). |
fbell_hz(shape, f, q, gain) |
1 | 1 | Feedback biquad bell equalizer (2nd order) with feedback shape, center f Hz, Q value q and amplitude gain gain. |
fdn(x) |
x |
x |
Feedback Delay Network: enclose feedback circuit x (with equal number of inputs and outputs) using diffusive Hadamard feedback. |
fdn2(x, y) |
x, y |
x, y |
Feedback Delay Network: enclose feedback circuit x (with equal number of inputs and outputs) using diffusive Hadamard feedback, with extra feedback loop processing y. The feedforward path does not include y. |
feedback(x) |
x |
x |
Enclose (single sample) feedback circuit x (with equal number of inputs and outputs). |
feedback2(x, y) |
x, y |
x, y |
Enclose (single sample) feedback circuit x (with equal number of inputs and outputs) with extra feedback loop processing y. The feedforward path does not include y. |
fir(weights) |
1 | 1 | FIR filter with the specified weights, for example, fir((0.5, 0.5)). |
fir3(gain) |
1 | 1 | Symmetric 3-point FIR calculated from desired gain at the Nyquist frequency. |
flanger(fb, min_d, max_d, f) |
1 | 1 | Flanger effect with feedback amount fb, minimum delay min_d seconds, maximum delay max_d seconds and delay function f, e.g., |t| lerp11(0.01, 0.02, sin_hz(0.1, t)). |
fhighpass(shape) |
3 (audio, frequency, Q) | 1 | Feedback biquad highpass (2nd order) with feedback shape, for example, Softsign(1.0). |
fhighpass_hz(shape, f, q) |
1 | 1 | Feedback biquad highpass (2nd order) with feedback shape, center f Hz and Q q. |
flowpass(shape) |
3 (audio, frequency, Q) | 1 | Feedback biquad lowpass (2nd order) with feedback shape, for example, Softsign(1.0). |
flowpass_hz(shape, f, q) |
1 | 1 | Feedback biquad lowpass (2nd order) with feedback shape, center f Hz and Q q. |
follow(t) |
1 | 1 | Smoothing filter with halfway response time t seconds. |
fresonator(shape) |
3 (audio, frequency, Q) | 1 | Feedback biquad resonator (2nd order) with feedback shape, for example, Softsign(1.0). |
fresonator_hz(shape, f, q) |
1 | 1 | Feedback biquad resonator (2nd order) with feedback shape, center f Hz and Q q. |
hammond() |
1 (frequency) | 1 | Bandlimited Hammond oscillator. Emphasizes first three partials. |
hammond_hz(f) |
- | 1 | Bandlimited Hammond oscillator at f Hz. Emphasizes first three partials. |
highpass() |
3 (audio, frequency, Q) | 1 | Highpass filter (2nd order). |
highpass_hz(f, q) |
1 | 1 | Highpass filter (2nd order) with cutoff frequency f Hz and Q q. |
highpass_q(q) |
2 (audio, frequency) | 1 | Highpass filter (2nd order) with Q q. |
highpole() |
2 (audio, frequency) | 1 | Highpass filter (1st order). |
highpole_hz(f) |
1 | 1 | Highpass filter (1st order) with cutoff frequency f Hz. |
highshelf() |
4 (audio, frequency, Q, gain) | 1 | High shelf filter (2nd order) with adjustable amplitude gain. |
highshelf_hz(f, q, gain) |
1 | 1 | High shelf filter (2nd order) centered at f Hz with Q q and amplitude gain gain. |
highshelf_q(q, gain) |
2 (audio, frequency) | 1 | High shelf filter (2nd order) with Q q and amplitude gain gain. |
hold(v) |
2 (signal, frequency) | 1 | Sample-and-hold component with hold time variability v in 0...1. |
hold_hz(f, v) |
1 | 1 | Sample-and-hold component at f Hz with hold time variability v in 0...1. |
impulse::<U>() |
- | U |
U-channel impulse; on each channel the first sample is one, the rest are zeros. |
join::<U>() |
U |
1 | Average together U channels. Inverse of split. |
lfo(f) |
- | f |
Time-varying control f with scalar or tuple output, e.g., |t| exp(-t). Synonymous with envelope. |
lfo2(f) |
1 (x) | f |
Time-varying, input dependent control f with scalar or tuple output, e.g., |t, x| exp(-t * x). Synonymous with envelope2. |
lfo3(f) |
2 (x, y) | f |
Time-varying, input dependent control f with scalar or tuple output, e.g., |t, x, y| y * exp(-t * x). Synonymous with envelope3. |
lfo_in(f) |
f |
f |
Time-varying, input dependent control f with scalar or tuple output, e.g., |t, i: &Frame<f32, U1>| exp(-t * i[0]). Synonymous with envelope_in. |
limiter(a, r) |
1 | 1 | Look-ahead limiter with attack time (and latency) a seconds and release time r seconds. |
limiter_stereo(a, r) |
2 | 2 | Stereo look-ahead limiter with attack time (and latency) a seconds and release time r seconds. |
lorenz() |
1 (frequency) | 1 | Lorenz dynamical system oscillator. |
lowpass() |
3 (audio, frequency, Q) | 1 | Lowpass filter (2nd order). |
lowpass_hz(f, q) |
1 | 1 | Lowpass filter (2nd order) with cutoff frequency f Hz and Q q. |
lowpass_q(q) |
2 (audio, frequency) | 1 | Lowpass filter (2nd order) with Q q. |
lowpole() |
2 (audio, frequency) | 1 | 1-pole lowpass filter (1st order). |
lowpole_hz(f) |
1 | 1 | 1-pole lowpass filter (1st order) with cutoff frequency f Hz. |
lowrez() |
3 (audio, frequency, Q) | 1 | Resonant lowpass filter (2nd order). |
lowrez_hz(f, q) |
1 | 1 | Resonant lowpass filter (2nd order) centered at f Hz with resonance q in 0...1. |
lowrez_q(q) |
2 (audio, frequency) | 1 | Resonant lowpass filter (2nd order) with resonance q in 0...1. |
lowshelf() |
4 (audio, frequency, Q, gain) | 1 | Low shelf filter (2nd order) with adjustable amplitude gain. |
lowshelf_hz(f, q, gain) |
1 | 1 | Low shelf filter (2nd order) centered at f Hz with Q q and amplitude gain gain. |
lowshelf_q(q, gain) |
2 (audio, frequency) | 1 | Low shelf filter (2nd order) with Q q and amplitude gain gain. |
map(f) |
f |
f |
Map channels freely, e.g., map(|i: &Frame<f32, U2>| max(i[0], i[1])). |
meter(mode) |
1 | 1 (meter) | Analyze input and output a summary according to the metering mode. |
mls() |
- | 1 | White MLS noise source. |
mls_bits(n) |
- | 1 | White MLS noise source from n-bit MLS sequence (1 <= n <= 31). |
monitor(&shared, mode) |
1 | 1 | Pass-through node that analyzes data passed through, storing a summary into the shared variable. |
moog() |
3 (audio, frequency, Q) | 1 | Moog resonant lowpass filter (4th order). |
moog_hz(f, q) |
1 | 1 | Moog resonant lowpass filter (4th order) with cutoff frequency f and resonance q. |
moog_q(q) |
2 (audio, frequency) | 1 | Moog resonant lowpass filter (4th order) with resonance q. |
morph() |
4 (audio, frequency, Q, morph) | 1 | Morphing filter with morph input in -1...1 (-1 = lowpass, 0 = peaking, 1 = highpass) |
morph_hz(f, q, morph) |
1 | 1 | Morphing filter with center frequency f, Q q and morph morph in -1...1 (-1 = lowpass, 0 = peaking, 1 = highpass) |
mul(x) |
x |
x |
Multiply signal with constant x. |
multijoin::<M, N>() |
M * N |
M |
Average N branches of M channels into one. Inverse of multisplit. |
multipass::<U>() |
U |
U |
Pass multichannel signal through. |
multisink::<U>() |
U |
- | Consumes multichannel signal. |
multisplit::<M, N>() |
M |
M * N |
Split M channels into N branches. |
multitap::<N>(min_delay, max_delay) |
N + 1 (audio, delay...) |
1 | Tapped delay line with cubic interpolation. Number of taps is N. |
multitap_linear::<N>(min_delay, max_delay) |
N + 1 (audio, delay...) |
1 | Tapped delay line with linear interpolation. Number of taps is N. |
multitick::<U>() |
U |
U |
Multichannel single sample delay. |
multizero::<U>() |
- | U |
Multichannel zero signal. |
noise() |
- | 1 | White noise source. Synonymous with white. |
notch() |
3 (audio, frequency, Q) | 1 | Notch filter (2nd order). |
notch_hz(f, q) |
1 | 1 | Notch filter (2nd order) centered at f Hz with Q q. |
notch_q(q) |
2 (audio, frequency) | 1 | Notch filter (2nd order) with Q q. |
organ() |
1 (frequency) | 1 | Bandlimited organ wave oscillator. |
organ_hz(f) |
- | 1 | Bandlimited organ wave oscillator at f Hz. |
oversample(node) |
node |
node |
2x oversample enclosed node. |
pan(pan) |
1 | 2 | Fixed mono-to-stereo equal power panner with pan in -1...1. |
panner() |
2 (audio, pan) | 2 | Mono-to-stereo equal power panner with pan in -1...1. |
pass() |
1 | 1 | Pass signal through. |
peak() |
3 (audio, frequency, Q) | 1 | Peaking filter (2nd order). |
peak_hz(f, q) |
1 | 1 | Peaking filter (2nd order) centered at f Hz with Q q. |
peak_q(q) |
2 (audio, frequency) | 1 | Peaking filter (2nd order) with Q q. |
phaser(fb, f) |
1 | 1 | Phaser effect with feedback amount fb and modulation function f, e.g., |t| sin_hz(0.1, t) * 0.5 + 0.5. |
pink() |
- | 1 | Pink noise source. |
pinkpass() |
1 | 1 | Pinking filter (3 dB/octave lowpass). |
pipe(x, y) |
x |
y |
Pipe x to y. Identical with x >> y. |
pipei::<U, _, _>(f) |
f |
f |
Chain U nodes from indexed generator f. |
pipef::<U, _, _>(f) |
f |
f |
Chain U nodes from fractional generator f. |
pluck(f, gain, damping) |
1 (excitation) | 1 | Karplus-Strong plucked string oscillator with frequency f Hz, gain per second (gain <= 1) and high frequency damping in 0...1. |
product(x, y) |
x + y |
x = y |
Multiply nodes x and y. Same as x * y. |
pulse() |
2 (frequency, duty cycle) | 1 | Bandlimited pulse wave with duty cycle in 0...1. |
ramp() |
1 (frequency) | 1 | Non-bandlimited ramp (sawtooth) wave in 0...1. |
ramp_hz(f) |
0 | 1 | Non-bandlimited ramp (sawtooth) wave in 0...1 with frequency f Hz. |
ramp_phase(phase) |
1 (frequency) | 1 | Non-bandlimited ramp (sawtooth) wave in 0...1 with initial phase in 0...1. |
ramp_hz_phase(f, phase) |
0 | 1 | Non-bandlimited ramp (sawtooth) wave in 0...1 with frequency f Hz and initial phase in 0...1. |
resample(node) |
1 (speed) | node |
Resample generator node using cubic interpolation at speed obtained from the input, where 1 is the original speed. |
resonator() |
3 (audio, frequency, Q) | 1 | Constant-gain bandpass resonator (2nd order). |
resonator_hz(f, q) |
1 | 1 | Constant-gain bandpass resonator (2nd order) with center frequency f Hz and Q q. |
resynth::<I, O, _>(w, f) |
I |
O |
Frequency domain resynthesis with window length w and processing function f. |
reverb_stereo(r, t, d) |
2 | 2 | Stereo reverb (32-channel FDN) with room size r meters (10 is average), reverberation time t seconds and high frequency damping d (in 0...1). |
reverb2_stereo(r, t, d, m, f) |
2 | 2 | Another stereo reverb (32-channel hybrid FDN) with room size r meters (10-30 meters is supported), reverberation time t seconds, diffusion amount d (in 0...1), modulation speed m (nominal range 0...1, beyond starts being an effect), and loop filter f. |
reverb3_stereo(t, d, f) |
2 | 2 | Another stereo reverb (allpass loop) with reverberation time t seconds, diffusion amount d (in 0...1), and loop filter f. |
reverse::<N>() |
N |
N |
Reverse channel order, e.g., swap left and right channels. |
rossler() |
1 (frequency) | 1 | Rössler dynamical system oscillator. |
rotate(a, g) |
2 | 2 | Rotate stereo signal a radians with gain g. |
saw() |
1 (frequency) | 1 | Bandlimited saw wave oscillator. |
saw_hz(f) |
- | 1 | Bandlimited saw wave oscillator at f Hz. |
shape(mode) |
1 | 1 | Shape signal with waveshaper mode mode. |
shape_fn(f) |
1 | 1 | Shape signal with waveshaper function f, e.g., tanh. |
sine() |
1 (frequency) | 1 | Sine oscillator. |
sine_hz(f) |
- | 1 | Sine oscillator at f Hz. |
sine_phase(p) |
1 (frequency) | 1 | Sine oscillator with initial phase p in 0...1. |
sink() |
1 | - | Consume signal. |
soft_saw() |
1 (frequency) | 1 | Bandlimited soft saw wave oscillator. |
soft_saw_hz(f) |
- | 1 | Bandlimited soft saw wave oscillator at f Hz. |
split::<U>() |
1 | U |
Split signal into U channels. |
square() |
1 (frequency) | 1 | Bandlimited square wave oscillator. |
square_hz(f) |
- | 1 | Bandlimited square wave oscillator at frequency f Hz. |
stack(x, y) |
x + y |
x + y |
Stack x and y. Identical with x | y. |
stacki::<U, _, _>(f) |
U * f |
U * f |
Stack U nodes from indexed generator f. |
stackf::<U, _, _>(f) |
U * f |
U * f |
Stack U nodes from fractional generator f, e.g., | x | delay(xerp(0.1, 0.2, x)). |
sub(x) |
x |
x |
Subtract constant x from signal. |
sum(x, y) |
x + y |
x = y |
Add nodes x and y. Same as x + y. |
sumi::<U, _, _>(f) |
U * f |
f |
Sum U nodes from indexed generator f. |
sumf::<U, _, _>(f) |
U * f |
f |
Sum U nodes from fractional generator f, e.g., | x | delay(xerp(0.1, 0.2, x)). |
tap(min_delay, max_delay) |
2 (audio, delay) | 1 | Tapped delay line with cubic interpolation. All times are in seconds. |
tap_linear(min_delay, max_delay) |
2 (audio, delay) | 1 | Tapped delay line with linear interpolation. All times are in seconds. |
thru(x) |
x |
x inputs |
Pass through missing outputs. Same as !x. |
tick() |
1 | 1 | Single sample delay. |
timer(&shared) |
- | - | Maintain current stream time in a shared variable. |
triangle() |
1 (frequency) | 1 | Bandlimited triangle wave oscillator. |
triangle_hz(f) |
- | 1 | Bandlimited triangle wave oscillator at f Hz. |
unit::<I, O>(unit) |
I |
O |
Convert an AudioUnit into an AudioNode with I inputs and O outputs. |
update(x, dt, f) |
x |
x |
Update node x with update interval dt seconds and update function f(t, dt, x). |
var(&shared) |
- | 1 | Output value of the shared variable. |
var_fn(&shared, f) |
- | f |
Output value of the shared variable mapped through function f. |
wavech(&wave, channel, loop) |
- | 1 | Play back a channel of Arc<Wave>. Optional loop point is the index to jump to at the end of the wave. |
wavech_at(&wave, channel, start, end, loop) |
- | 1 | Play back a channel of Arc<Wave> between indices start (inclusive) and end (exclusive), with optional loop index to jump to at the end. |
white() |
- | 1 | White noise source. Synonymous with noise. |
zero() |
- | 1 | Zero signal. |
Subsampled Controls
envelope is a node that samples a time varying control function.
For example, envelope(|t| exp(-t)) is an exponentially decaying envelope.
A control function is something that is expected to change relatively slowly.
Therefore, we can save time by not calling it at every sample.
The argument to the function is time in seconds. Whenever the node is reset, time resets to zero.
envelope is generic over channel arity:
The return type of the function - scalar or tuple - determines the number of outputs.
The samples are spaced at an average of 2 ms apart, jittered by noise derived from pseudorandom phase. The values in between are linearly interpolated.
lfo (Low Frequency Oscillator) is another name for envelope.
Indexed And Fractional Generator Functions
branchi, busi, pipei, sumi and stacki are opcodes that combine multiple nodes of the same type.
The number of nodes is their first generic argument.
They accept a generator function that is issued u64 integers starting from 0.
The nodes are allocated inline, and each node is assigned its own pseudorandom phase.
For example, to create 20 noise bands in 1 kHz...2 kHz:
use fundsp::hacker::*;
let partials = busi::<U20, _, _>(|i| noise() >> resonator_hz(xerp(1_000.0, 2_000.0, rnd1(i) as f32), 20.0));
Similarly, branchf, busf, pipef, sumf and stackf accept a generator function
that is issued values evenly distributed in the unit interval 0...1.
The first node is issued the value 0 and the last node the value 1.
If there is only one node, then it receives the value 0.5.
For example, to distribute 20 noise bands evenly in 1 kHz...2 kHz:
use fundsp::hacker::*;
let partials = busf::<U20, _, _>(|f| noise() >> resonator_hz(xerp(1_000.0, 2_000.0, f), 20.0));
Waveshaping Modes
These are arguments to the shape opcode. Shapes Atan, Clip, Softsign and Tanh
all have a slope of 1 at the origin when hardness is 1, saturate in the range -1...1,
and are nonexpansive up to a hardness of 1.
Adaptive::new(timescale, inner): Apply adaptive normalizing distortion with smoothingtimescalein seconds. Smoothing timescale is the time it takes for level estimation to move halfway to a new value. The argument to theinnershape is divided by the RMS level of the signal.Atan(hardness): Applyatandistortion with configurable hardness, with the output range scaled to -1...1. Argument toatanis multiplied by the hardness value.Clip(hardness): Multiply signal with hardness and then clamp it to -1...1.ClipTo(minimum, maximum): Clip signal between the two arguments.Crush(levels): Apply a staircase function with configurable number of levels per unit.SoftCrush(levels): Apply a smooth staircase function with configurable number of levels per unit.Softsign(hardness): Applysoftsigndistortion with configurable hardness. Argument tosoftsignis multiplied by the hardness value.Tanh(hardness): Applytanhdistortion with configurable hardness. Argument totanhis multiplied by the hardness value.
Metering Modes
The monitor(&shared, mode) opcode is a pass-through node that presents
some aspect of data passed through in a shared variable. Metering modes are:
Meter::Sample: Stores the latest value passed through.Meter::Peak(timescale): Peak amplitude meter with smoothingtimescalein seconds.Meter::Rms(timescale): Root mean square meter with smoothingtimescalein seconds.
Smoothing timescale is the time it takes for level estimation to move halfway to a new value.
The same modes are used in the meter opcode.
Math And Utility Functions
| Function | Explanation |
|---|---|
a_weight(f) |
A-weighted amplitude response at f Hz (normalized to 1.0 at 1 kHz) |
abs(x) |
absolute value of x |
amp_db(x) |
convert amplitude (aka gain) x to decibels with amplitude 1.0 equal to 0 dB |
bpm_hz(bpm) |
convert bpm BPM (beats per minute) to Hz |
ceil(x) |
ceiling function |
clamp(min, max, x) |
clamp x between min and max |
clamp01(x) |
clamp x between 0 and 1 |
clamp11(x) |
clamp x between -1 and 1 |
cos(x) |
cos |
cos_hz(f, t) |
cosine that oscillates at f Hz at time t seconds |
cubed(x) |
cube of x |
db_amp(x) |
convert x dB to amplitude (aka gain) with 0 dB equal to amplitude 1.0 |
delerp(x0, x1, x) |
recover linear interpolation amount t in 0...1 from interpolated value |
delerp11(x0, x1, x) |
recover linear interpolation amount t in -1...1 from interpolated value |
dexerp(x0, x1, x) |
recover exponential interpolation amount t in 0...1 from interpolated value (x0, x1, x > 0) |
dexerp11(x0, x1, x) |
recover exponential interpolation amount t in -1...1 from interpolated value (x0, x1, x > 0) |
dissonance(f0, f1) |
dissonance amount in 0...1 between pure tones at f0 and f1 Hz |
dissonance_max(f) |
maximally dissonant pure frequency above f Hz |
downarc(x) |
concave quarter circle easing curve (inverse function of uparc in 0...1) |
ease_noise(ease, seed, x) |
value noise in -1...1 interpolated with easing function ease, e.g., smooth3 |
ease_noise((rise, fall), seed, x) |
value noise in -1...1 interpolated with easing function rise in rising segments and fall in falling segments, e.g., (uparc, downarc) |
exp(x) |
exp |
exp10(x) |
10 to the power of x |
exp2(x) |
2 to the power of x |
floor(x) |
floor function |
fract(x) |
fract function |
fractal_noise(seed, octaves, roughness, x) |
fractal spline noise (octaves > 0, roughness > 0) |
fractal_ease_noise(ease, seed, octaves, roughness, x) |
fractal ease noise (octaves > 0, roughness > 0) interpolated with easing function ease |
hash1(x) |
u64 hashing function which is a pseudorandom permutation |
hash2(x) |
u64 hashing function which is a pseudorandom permutation |
identity(x) |
identity function (linear easing function) |
lerp(x0, x1, t) |
linear interpolation between x0 and x1 with t in 0...1 |
lerp11(x0, x1, t) |
linear interpolation between x0 and x1 with t in -1...1 |
log(x) |
natural logarithm |
log10(x) |
base 10 logarithm |
log2(x) |
binary logarithm |
midi_hz(x) |
convert MIDI note number x to Hz (69.0 = A4 = 440 Hz) |
min(x, y) |
minimum of x and y |
max(x, y) |
maximum of x and y |
m_weight(f) |
M-weighted amplitude response at f Hz (normalized to 1.0 at 1 kHz) |
pow(x, y) |
x raised to the power y |
rnd1(i) |
pseudorandom number in 0...1 from integer i |
rnd2(i) |
pseudorandom number in 0...1 from integer i |
round(x) |
round x to nearest integer |
semitone_ratio(x) |
convert interval x semitones to frequency ratio |
signum(x) |
sign of x |
sin(x) |
sin |
sin_hz(f, t) |
sine that oscillates at f Hz at time t seconds |
smooth3(x) |
smooth cubic easing polynomial |
smooth5(x) |
smooth 5th degree easing polynomial (commonly used in computer graphics) |
smooth7(x) |
smooth 7th degree easing polynomial |
smooth9(x) |
smooth 9th degree easing polynomial |
softexp(x) |
polynomial alternative to exp |
softmix(x, y, bias) |
weighted average of x and y according to bias: polynomial softmin when bias < 0, average when bias = 0, polynomial softmax when bias > 0 |
softsign(x) |
softsign function, a polynomial alternative to tanh |
squared(x) |
square of x |
sqr_hz(f, t) |
square wave (non-bandlimited) that oscillates at f Hz at time t seconds |
sqrt(x) |
square root of x |
spline(x0, x1, x2, x3, t) |
Catmull-Rom cubic interpolation between x1 and x2, taking x0 and x3 into account |
spline_mono(x0, x1, x2, x3, t) |
monotonic cubic interpolation between x1 and x2, taking x0 and x3 into account |
spline_noise(seed, x) |
value noise in -1...1 interpolated with a cubic spline, with one interpolation point per integer cell |
tan(x) |
tan |
tanh(x) |
hyperbolic tangent |
tri_hz(f, t) |
triangle wave (non-bandlimited) that oscillates at f Hz at time t seconds |
uparc(x) |
convex quarter circle easing curve (inverse function of downarc in 0...1) |
xerp(x0, x1, t) |
exponential interpolation between x0 and x1 (x0, x1 > 0) with t in 0...1 |
xerp11(x0, x1, t) |
exponential interpolation between x0 and x1 (x0, x1 > 0) with t in -1...1 |
Easing Functions
Easing functions are interpolation curves that remap the range 0...1. These math functions have the shape of an easing function.
| Function | Explanation |
|---|---|
cubed(x) |
cube of x |
downarc(x) |
concave quarter circle easing curve (inverse function of uparc in 0...1) |
identity(x) |
identity function (linear easing function) |
smooth3(x) |
smooth cubic easing polynomial |
smooth5(x) |
smooth 5th degree easing polynomial (commonly used in computer graphics) |
smooth7(x) |
smooth 7th degree easing polynomial |
smooth9(x) |
smooth 9th degree easing polynomial |
squared(x) |
square of x |
sqrt(x) |
square root of x |
uparc(x) |
convex quarter circle easing curve (inverse function of downarc in 0...1) |

For example, if we wish to interpolate a transition, then interpolation, de-interpolation and re-interpolation combined with easing functions is handy. This example defines an inaudible tone suppression function for pure tones, falling smoothly from one at 20 kHz to zero at the default Nyquist frequency of 22.05 kHz.
use fundsp::hacker::*;
fn pure_tone_amp(hz: f32) -> f32 { lerp(1.0, 0.0, smooth5(clamp01(delerp(20_000.0, 22_050.0, hz)))) }
The above is an example of re-interpolation, which is de-interpolation followed with interpolation. First we recover, using delerp and clamping, an interpolation value in 0...1 (this is de-interpolation). Then we interpolate that value smoothly using lerp with the smooth5 ease, in the desired final range of 1 to 0.
For exponential interpolation and de-interpolation, such as might be often used to deal with amplitudes or frequencies, use the xerp and dexerp functions.
Noise Functions

Examples
Some examples of graph expressions.
| Expression | Inputs | Outputs | Meaning |
|---|---|---|---|
pass() ^ pass() |
1 | 2 | mono-to-stereo splitter |
split::<U2>() |
1 | 2 | -..- |
mul(0.5) + mul(0.5) |
2 | 1 | stereo-to-mono mixdown (inverse of mono-to-stereo splitter) |
join::<U2>() |
2 | 1 | -..- |
pass() ^ pass() ^ pass() |
1 | 3 | mono-to-trio splitter |
split::<U3>() |
1 | 3 | -..- |
sink() | zero() |
1 | 1 | replace signal with silence |
mul(0.0) |
1 | 1 | -..- |
mul(db_amp(3.0)) |
1 | 1 | amplify signal by 3 dB |
sink() | pass() |
2 | 1 | extract right channel |
pass() | sink() |
2 | 1 | extract left channel |
sink() | zero() | pass() |
2 | 2 | replace left channel with silence |
mul(0.0) | pass() |
2 | 2 | -..- |
mul((0.0, 1.0)) |
2 | 2 | -..- |
pass() | sink() | zero() |
2 | 2 | replace right channel with silence |
pass() | mul(0.0) |
2 | 2 | -..- |
mul((1.0, 0.0)) |
2 | 2 | -..- |
(pass() & tick()) * 0.5 |
1 | 1 | 2-point averaging FIR filter |
fir((0.5, 0.5)) |
1 | 1 | -..- |
fir(Frame::from([0.5, 0.5])) |
1 | 1 | -..- |
!butterpass() >> lowpole() |
2 | 1 | 2nd order and 1-pole lowpass filters in series (3rd order) |
!butterpass() >> !butterpass() >> butterpass() |
2 | 1 | triple lowpass filter in series (6th order) |
!resonator() >> resonator() |
3 | 1 | double resonator in series (4th order) |
oversample(sine_hz(f) * f * m + f >> sine()) |
- | 1 | Oversampled FM (frequency modulation) oscillator at f Hz with modulation index m |
sine() & mul(2.0) >> sine() |
1 | 1 | frequency doubled dual sine oscillator |
envelope(|t| exp(-t)) * noise() |
- | 1 | exponentially decaying white noise |
lfo(|t| xerp11(0.25, 4.0, spline_noise(1, t))) >> resample(pink()) |
0 | 1 | Resampled pink noise. |
feedback(delay(1.0) * db_amp(-3.0)) |
1 | 1 | 1 second feedback delay with 3 dB attenuation |
feedback((delay(1.0) | delay(1.0)) >> reverse() * db_amp(-6.0)) |
2 | 2 | 1 second ping-pong delay with 6 dB attenuation. |
var(&wet) * delay(1.0) & (1.0 - var(&wet)) * pass() |
1 | 1 | 1 second delay with wet/dry mix controlled by shared variable wet. The shared variable can be declared as let wet = shared(0.5); |
sine() & mul(semitone_ratio(4.0)) >> sine() & mul(semitone_ratio(7.0)) >> sine() |
1 | 1 | major chord |
dc(midi_hz(72.0)) >> sine() & dc(midi_hz(76.0)) >> sine() & dc(midi_hz(79.0)) >> sine() |
0 | 1 | C major chord generator |
!zero() |
0 | 0 | A null node. Stacking it with another node modifies its sound subtly, as the hash is altered. |
!-!!!--!!!-!!--!zero() |
0 | 0 | Hot-rodded null node outfitted with a custom hash. Uses more electricity. |
Examples From The Prelude
Many functions in the prelude itself are defined as graph expressions.
| Function | Inputs | Outputs | Definition |
|---|---|---|---|
brown() |
- | 1 | white() >> lowpole_hz(10.0) * constant(13.7) |
mls() |
- | 1 | mls_bits(29) |
pink() |
- | 1 | white() >> pinkpass() |
saw_hz(f) |
- | 1 | constant(f) >> saw() |
sine_hz(f) |
- | 1 | constant(f) >> sine() |
square_hz(f) |
- | 1 | constant(f) >> square() |
triangle_hz(f) |
- | 1 | constant(f) >> triangle() |
zero() |
- | 1 | constant(0.0) |
Equivalent Expressions
There are usually many ways to express a particular graph. The following expression pairs are identical.
| Expression | Is The Same As | Notes |
|---|---|---|
(pass() ^ mul(2.0)) >> sine() + sine() |
sine() & mul(2.0) >> sine() |
Busing is often more convenient than explicit branching followed with summing. |
--sink()-42.0^sink()&---sink()*3.14 |
sink() |
Branching, busing and arithmetic on sinks are no-ops. |
constant(0.0) | dc(1.0) |
constant((0.0, 1.0)) |
Stacking concatenates channels. |
sink() | zero() |
zero() | sink() |
The order does not matter because sink() only adds an input, while zero() only adds an output. |
(butterpass() ^ (sink() | pass())) >> butterpass() |
!butterpass() >> butterpass() |
Running a manual bypass. |
!sink() |
pass() |
The attempt of the sink to consume signal is foiled by the thru operator, which passes the missing output through. |
!(noise() | noise()) |
!noise() |
The thru operator nullifies any generator. |
Audio Graph Types
The AudioNode component system represents audio network structure at the type level.
The representation contains input and output arities,
which are encoded as types U0, U1, ..., by the typenum crate.
The associated types are AudioNode::Inputs and AudioNode::Outputs.
The preludes employ the wrapper type An<X: AudioNode>
containing operator overloads and other trait implementations.
The wrapper also implements the AudioUnit trait.
The type encoding is straightforward. As an example, in the hacker prelude
noise() & constant(440.0) >> sine()
is represented as
An<Bus<Noise, Pipe<Constant<U1>, Sine>>>
The compiler reports these types in an opaque form.
An attached utility, examples/type.rs, can unscramble such opaque types.
This invocation prints the above type:
cargo run --example type -- "fundsp::combinator::An<Bus<Noise, Pipe<Constant<typenum::uint::UInt<typenum::uint::UTerm,typenum::bit::B1>>, Sine>>>"
It is also possible to declare the return type as an impl AudioNode.
However, this type is also opaque and cannot be stored as an AudioNode;
conversion to AudioUnit may be necessary in this case.
Declaring the full arity in the signature does enable use of the node in further combinations. For example:
use fundsp::hacker::*;
fn split_quad() -> An<impl AudioNode<Inputs = U1, Outputs = U4>> {
pass() ^ pass() ^ pass() ^ pass()
}
License
Licensed under either of Apache License, Version 2.0 or MIT license at your option.
Unless you explicitly state otherwise, any contribution intentionally submitted for inclusion in FunDSP by you, as defined in the Apache-2.0 license, shall be dual licensed as above, without any additional terms or conditions.
Dependencies
~16MB
~358K SLoC