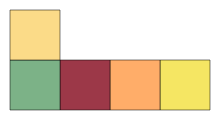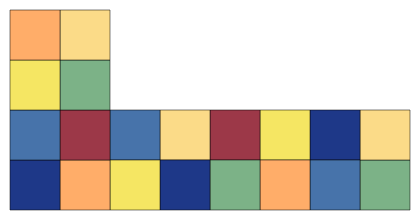3 releases
| 0.1.2 | Nov 2, 2019 |
|---|---|
| 0.1.1 | Aug 22, 2019 |
| 0.1.0 | Aug 22, 2019 |
#379 in Graphics APIs
56KB
1K
SLoC
dcc-tiler
Basic tile terminology
There are currently two types of tiles supported, which are explained below.
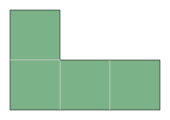
LTile
An LTile of size n is the L-tetronimo with n + 1 blocks. For example
anLTile of size 3 is:
while an LTile of size 5 is:
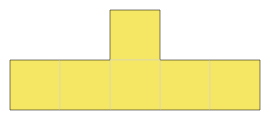
TTile
A TTile of size n is the T-tetronimo with 2(n+1) blocks. For example, a TTile of size 1 is:
while a TTile of size 2 is:
Basic board terminology
There are currently three supported boards: Rectangle, LBoard, and TBoard.
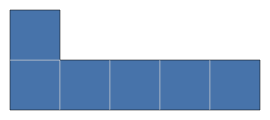
LBoard and TBoard
There are two parameters that affect the shape/size of an L/T board: board_size and board_scale.
With these parameters, a tile (either L or T) of size board_size is created, and then each
box in this tile is replaced by board_scale ** 2 boxes.
For example, an LBoard with size 4 and scale 1 looks like:
while bumping the scale up to 2 results in:
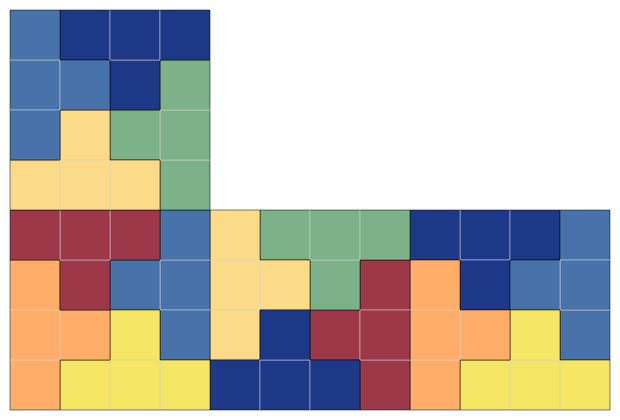
A TBoard with size 1 and scale 1 looks like:
while bumping the scale up to 2 results in:
Rectangle
There are two parameters that affect the shape/size of a rectangular board: board_size (height) and width.
For example, a Rectangle with board_size = 3 and width = 5 looks like:
While a Rectangle with board_size = 6 and width = 4 looks like:
Note: The scale parameter is ignored for Rectangle.
Counting tilings of an LBoard by LTiles
The following command counts the number of tilings of an LBoard of size 2 by LTile's of size 2,
with scale parameter x:
dcc_tiler_cli --count --scale x --board_type LBoard --tile_type LTile 2 2
This results in the following tiling counts as x varies:
x |
Tilings |
|---|---|
| 1 | 1 |
| 2 | 1 |
| 3 | 4 |
| 4 | 409 |
| 5 | 108388 |
| 6 | 104574902 |
| 7 | 608850350072 |
| 8 | 19464993703121249 |
This sequence of integers (1, 1, 4, 409, ...) does not appear in the OEIS.
Counting tilings of a TBoard by TTiles
The command here is:
dcc_tiler_cli --count --scale x --board_type TBoard --tile_type TTile 1 1
Exercise: Show that if x > 1 and x % 4 != 0 then there are no such tilings!
This results in the following tiling counts as x varies:
x |
Tilings |
|---|---|
| 1 | 1 |
| 4 | 54 |
| 8 | 655302180 |
| 12 | ? |
Alternative approach
Instead of modifying the scale parameter each time, you can instead use the --scaling option as follows:
dcc_tiler_cli --scaling --board_type TBoard --tile_type TTile 1 1
which results in the following output:
scale(1), 1 tilings
scale(2), 0 tilings
scale(3), 0 tilings
scale(4), 54 tilings
scale(5), 0 tilings
scale(6), 0 tilings
scale(7), 0 tilings
scale(8), 655302180 tilings
...
Counting tilings of an LBoard by TTiles
Many combinations are possible. An example is:
dcc_tiler_cli --count --scale 4 --board_type LBoard --tile_type TTile 3 1
which counts 54 tilings. An example of such a tiling is:
Counting tilings of a rectangle by TTiles
Suppose we wanted to count how many ways there are to tile an n x n rectangle
using T-tetronimos of size 1. The command here is:
dcc_tiler_cli --count --board_type Rectangle --width n --tile_type TTile n 1
which results in the following output:
n |
Tilings |
|---|---|
| 4 | 2 |
| 8 | 84 |
| 12 | 78696 |
| 16 | 1668091536 |
| 20 | 804175873700640 |
| 24 | 8840889502844537044800 |
which agrees with the table appearing in C. Merino, 2008.
Generating a single tiling image
After counting the number of tilings, it is often useful to render an image of such a tiling for visual
inspection. We know from the previous section that there are 54 tilings of an LBoard of size 3, scale 4
by TTile's of size 1. To generate such a tiling, we use the --single option and pipe the output into output.svg:
dcc_tiler_cli --single --scale 4 --board_type LBoard --tile_type TTile 3 1 > output.svg
Note: The CLI generates at most 1000 tilings and then selects a single tiling to render from among them, so there is no guarantee that running this command repeatedly will generate all possible tilings.
Generate all tiling images
Instead of generating a single image, you can also generate a ZIP file containing all tilings using the --all <filename> command.
For example:
dcc_tiler_cli --all tilings.zip --scale 4 --board_type LBoard --tile_type TTile 3 1
Tiling graphs
It is possible to output all tiling data as a graph represented in JSON. A 4x8 rectangular board is represented by the JSON object:
{ "board" : [ [false, false, false, false],
[false, false, false, false],
[false, false, false, false],
[false, false, false, false],
[false, false, false, false],
[false, false, false, false],
[false, false, false, false],
[false, false, false, false], ] }
If we placed down a size 1 T-tetronimo in the top left corner of the board, our new board would be:
{ "board" : [ [true, true, true, false],
[false, true, false, false],
[false, false, false, false],
[false, false, false, false],
[false, false, false, false],
[false, false, false, false],
[false, false, false, false],
[false, false, false, false], ] }
The tiling graph consists of the following:
- An array
nodes_arenaconsisting of board objects (as above), - An object
edgesof the form:
{
"0": [ 1, 2 ],
"1" : [ 3 ],
"2" : [ 4 ],
"3" : [ 5, 7, 8, 6 ],
}
- An object
rev_edgesof the form:
{
"1": [ 0 ],
"2" : [ 0 ],
"3" : [ 1 ],
"4" : [ 2 ],
"5" : [ 3 ],
"6" : [ 3 ],
"7" : [ 3 ],
"8" : [ 3 ],
}
- An array
complete_indicesof the form:
[ 36 ]
Nodes in our graph correspond to the boards in node_arena, so the first entry in nodes_arena is node 0,
the second entry is node 1, and so on. Node 0 is always the empty board (no tiles). An edges s -> t between
two nodes indicates that you can get from board s to board t by placing down a tile. Such an edge
is recorded in two places: in the edges object (so that t is in edges[s]), and in the rev_edges
object (so that s is in rev_edges[t]). Finally, if a complete tiling is possible, its node will be stored in the complete_indices
array.
Things to note about tiling graphs:
-
If there are a lot of tilings, generating the graph can take a long time, and the resulting graph will generally be large and difficult to work with in memory. This problem is what motivated the
--countand--singlecommands, which avoid generating the entire tile graph. -
Given an edge
s -> twe don't store any data on which tile must be placed down to get from boardsto boardt; this can be recovered by looking at which entries switched fromfalsetotruein going fromstot. -
Suppose you wanted to count the number of possible ways to tile a board. Using the graph, one way to do this is as follows:
- Initialize a hash map
countwithcount[0] = 1(i.e. there is one way to tile the empty board). - Initialize a hash set
current_layerwith node0. - While
current_layeris nonempty:- Initialize an empty hash set
next_layer. - For each node
sincurrent_layer:- For each node
tinedges[s]:- If
tis not incount, setcount[t] = 0. - Increment
count[t]bycount[s]. - Add
ttonext_layer.
- If
- For each node
- Set
current_layer = next_layer.
- Initialize an empty hash set
- The total number of tilings will be
count[final], wherefinalis the node appearing incomplete_indices.
- Initialize a hash map
License
Licensed under either of
- Apache License, Version 2.0 (LICENSE-APACHE or http://www.apache.org/licenses/LICENSE-2.0)
- MIT license (LICENSE-MIT or http://opensource.org/licenses/MIT)
at your option.
Contribution
Unless you explicitly state otherwise, any contribution intentionally submitted for inclusion in the work by you, as defined in the Apache-2.0 license, shall be dual licensed as above, without any additional terms or conditions.
Dependencies
~6.5–9MB
~153K SLoC