11 unstable releases
| 0.6.3 | May 17, 2021 |
|---|---|
| 0.6.2 | Feb 10, 2020 |
| 0.6.1 | Nov 2, 2019 |
#500 in Algorithms
69KB
1K
SLoC
dcc-lsystem
A crate for working with Lindenmayer systems.
Background
An L-System consists of an alphabet of symbols that can be used to make strings, a collection of production rules that expand each symbol into a larger string of symbols, an initial axiom string from which to begin construction, and a mechanism for transforming the generated strings into geometric structures.
Algae example
Lindenmayer's original L-System for modelling the growth of Algae had
variables A and B, axiom A, and production rules A -> AB, B -> A. Iterating
this system produces the following output:
AABABAABAAB
Basic usage
Put the following in your Cargo.toml:
dcc-lsystem = "0.6"
LSystemBuilder
An L-system is represented by an instance of LSystem. To create a barebones LSystem,
the LSystemBuilder struct is useful. The following example shows an implementation of
Lindenmayer's Algae system.
use dcc_lsystem::LSystemBuilder;
let mut builder = LSystemBuilder::new();
// Set up the two tokens we use for our system.
let a = builder.token("A");
let b = builder.token("B");
// Set up our axiom (i.e. initial state)
builder.axiom(vec![a]);
// Set the transformation rules
builder.transformation_rule(a, vec![a,b]); // A -> AB
builder.transformation_rule(b, vec![a]); // B -> A
// Build our LSystem, which should have initial state A
let mut system = builder.finish();
assert_eq!(system.render(), "A");
// system.step() applies our production rules a single time
system.step();
assert_eq!(system.render(), "AB");
system.step();
assert_eq!(system.render(), "ABA");
// system.step_by() applies our production rule a number of times
system.step_by(5);
assert_eq!(system.render(), "ABAABABAABAABABAABABAABAABABAABAAB");
Rendering L-systems
It is possible to render an L-system into an image or gif. Typically this is done using
a turtle - each token in the L-system's state is associated with some movement or rotation
(or perhaps something more complicated) of a turtle. The TurtleLSystemBuilder struct offers
a convenient way of constructing such renderings.
Images
The Koch curve can be generated using an L-system with 3 symbols: F, +, and -,
where F corresponds to moving forwards, + denotes a left rotation by 90°,
and - denotes a right rotation by 90°. The system has axiom F and transformation
rule F => F+F-F-F+F. This is implemented in the following example.
use image::Rgb;
use dcc_lsystem::turtle::{TurtleLSystemBuilder, TurtleAction};
use dcc_lsystem::renderer::{ImageRendererOptions, Renderer};
let mut builder = TurtleLSystemBuilder::new();
builder
.token("F", TurtleAction::Forward(30)) // F => go forward 30 units
.token("+", TurtleAction::Rotate(90)) // + => rotate left 90°
.token("-", TurtleAction::Rotate(-90)) // - => rotate right 90°
.axiom("F")
.rule("F => F + F - F - F + F");
let (mut system, renderer) = builder.finish();
system.step_by(5); // Iterate our L-system 5 times
let options = ImageRendererOptionsBuilder::new()
.padding(10)
.thickness(4.0)
.fill_color(Rgb([255u8, 255u8, 255u8]))
.line_color(Rgb([0u8, 0u8, 100u8]))
.build();
renderer
.render(&system, &options)
.save("koch_curve.png")
.expect("Failed to save koch_curve.png");
The resulting image is shown in the Examples section below.
GIFs
It is also possible to render a GIF using an L-system. The individual frames of the GIF correspond to partial renderings of the L-system's state.
use image::Rgb;
use dcc_lsystem::renderer::{Renderer, VideoRendererOptions};
use dcc_lsystem::turtle::{TurtleAction, TurtleLSystemBuilder};
fn main() {
let mut builder = TurtleLSystemBuilder::new();
builder
.token("F", TurtleAction::Forward(30))
.token("+", TurtleAction::Rotate(90))
.token("-", TurtleAction::Rotate(-90))
.axiom("F")
.rule("F => F + F - F - F + F");
let (mut system, renderer) = builder.finish();
system.step_by(5);
let options = VideoRendererOptionsBuilder::new()
.filename("koch_curve.gif")
.fps(20)
.skip_by(0)
.padding(10)
.thickness(4.0)
.fill_color(Rgb([255u8, 255u8, 255u8]))
.line_color(Rgb([0u8, 0u8, 100u8]))
.progress_bar(true)
.build();
renderer
.render(&system, &options);
}
Turtle actions
Currently the following actions are available:
TurtleAction |
Description |
|---|---|
Nothing |
The turtle does nothing. |
Rotate(i32) |
Rotate the turtle through an angle. |
Forward(i32) |
Move the turtle forwards. |
Push |
Push the turtle's current heading and location onto the stack. |
Pop |
Pop the turtle's heading and location off the stack. |
StochasticRotate(Box<dyn Distribution>) |
Rotate the turtle through an angle specified by some probability distribution. |
StochasticForward(Box<dyn Distribution>) |
Move the turtle forwards through a distance specified by some probability distribution. |
The Distribution trait is given by:
pub trait Distribution: dyn_clone::DynClone {
fn sample(&self) -> i32;
}
A possible implementation of a Uniform distribution (using the rand crate) is as follows:
use rand::Rng;
#[derive(Clone)]
pub struct Uniform {
lower: i32,
upper: i32,
}
impl Uniform {
pub fn new(lower: i32, upper: i32) -> Self {
Self { lower, upper }
}
}
impl Distribution for Uniform {
fn sample(&self) -> i32 {
let mut rng = rand::thread_rng();
rng.gen_range(self.lower..=self.upper)
}
}
Examples
Examples are located in dcc-lsystem/examples.
Sierpinski Arrowhead

Koch curve
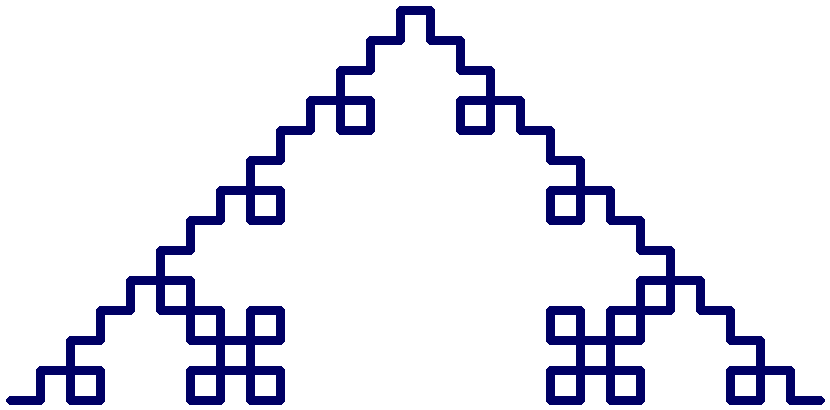
Dragon curve

Fractal plant

License
Licensed under either of
- Apache License, Version 2.0 (LICENSE-APACHE or http://www.apache.org/licenses/LICENSE-2.0)
- MIT license (LICENSE-MIT or http://opensource.org/licenses/MIT)
at your option.
Contribution
Unless you explicitly state otherwise, any contribution intentionally submitted for inclusion in the work by you, as defined in the Apache-2.0 license, shall be dual licensed as above, without any additional terms or conditions.
Dependencies
~6–18MB
~265K SLoC
