227 releases
| 0.39.5 | Apr 21, 2025 |
|---|---|
| 0.39.3 | Mar 13, 2025 |
| 0.39.0 |
|
| 0.37.9 | Jul 30, 2024 |
| 0.6.6 | Nov 29, 2018 |
#18 in Math
25,767 downloads per month
Used in 23 crates
(12 directly)
1MB
21K
SLoC
Peroxide
Rust numeric library contains linear algebra, numerical analysis, statistics and machine learning tools with R, MATLAB, Python like macros.
Table of Contents
- Why Peroxide?
- Latest README version
- Pre-requisite
- Install
- Useful tips for features
- Module Structure
- Documentation
- Examples
- Release Info
- Contributes Guide
- LICENSE
- TODO
Why Peroxide?
1. Customize features
Peroxide provides various features.
default- Pure Rust (No dependencies of architecture - Perfect cross compilation)O3- BLAS & LAPACK (Perfect performance but little bit hard to set-up - Strongly recommend to look Peroxide with BLAS)plot- With matplotlib of python, we can draw any plots.complex- With complex numbers (vector, matrix and integral)parallel- With some parallel functionsnc- To handle netcdf file format with DataFramecsv- To handle csv file format with Matrix or DataFrameparquet- To handle parquet file format with DataFrameserde- serialization with Serde.rkyv- serialization with rkyv.
If you want to do high performance computation and more linear algebra, then choose O3 feature.
If you don't want to depend C/C++ or Fortran libraries, then choose default feature.
If you want to draw plot with some great templates, then choose plot feature.
You can choose any features simultaneously.
2. Easy to optimize
Peroxide uses a 1D data structure to represent matrices, making it straightforward to integrate with BLAS (Basic Linear Algebra Subprograms). This means that Peroxide can guarantee excellent performance for linear algebraic computations by leveraging the optimized routines provided by BLAS.
3. Friendly syntax
For users familiar with numerical computing libraries like NumPy, MATLAB, or R, Rust's syntax might seem unfamiliar at first. This can make it more challenging to learn and use Rust libraries that heavily rely on Rust's unique features and syntax.
However, Peroxide aims to bridge this gap by providing a syntax that resembles the style of popular numerical computing environments. With Peroxide, you can perform complex computations using a syntax similar to that of R, NumPy, or MATLAB, making it easier for users from these backgrounds to adapt to Rust and take advantage of its performance benefits.
For example,
#[macro_use]
extern crate peroxide;
use peroxide::prelude::*;
fn main() {
// MATLAB like matrix constructor
let a = ml_matrix("1 2;3 4");
// R like matrix constructor (default)
let b = matrix(c!(1,2,3,4), 2, 2, Row);
// Or use zeros
let mut z = zeros(2, 2);
z[(0,0)] = 1.0;
z[(0,1)] = 2.0;
z[(1,0)] = 3.0;
z[(1,1)] = 4.0;
// Simple but effective operations
let c = a * b; // Matrix multiplication (BLAS integrated)
// Easy to pretty print
c.print();
// c[0] c[1]
// r[0] 1 3
// r[1] 2 4
// Easy to do linear algebra
c.det().print();
c.inv().print();
// and etc.
}
4. Can choose two different coding styles.
In peroxide, there are two different options.
prelude: To simple use.fuga: To choose numerical algorithms explicitly.
For examples, let's see norm.
In prelude, use norm is simple: a.norm(). But it only uses L2 norm for Vec<f64>. (For Matrix, Frobenius norm.)
#[macro_use]
extern crate peroxide;
use peroxide::prelude::*;
fn main() {
let a = c!(1, 2, 3);
let l2 = a.norm(); // L2 is default vector norm
assert_eq!(l2, 14f64.sqrt());
}
In fuga, use various norms. But you should write a little bit longer than prelude.
#[macro_use]
extern crate peroxide;
use peroxide::fuga::*;
fn main() {
let a = c!(1, 2, 3);
let l1 = a.norm(Norm::L1);
let l2 = a.norm(Norm::L2);
let l_inf = a.norm(Norm::LInf);
assert_eq!(l1, 6f64);
assert_eq!(l2, 14f64.sqrt());
assert_eq!(l_inf, 3f64);
}
5. Batteries included
Peroxide can do many things.
- Linear Algebra
- Effective Matrix structure
- Transpose, Determinant, Diagonal
- LU Decomposition, Inverse matrix, Block partitioning
- QR Decomposition (
O3feature) - Singular Value Decomposition (SVD) (
O3feature) - Cholesky Decomposition (
O3feature) - Reduced Row Echelon form
- Column, Row operations
- Eigenvalue, Eigenvector
- Functional Programming
- Easier functional programming with
Vec<f64> - For matrix, there are three maps
fmap: map for all elementscol_map: map for column vectorsrow_map: map for row vectors
- Easier functional programming with
- Automatic Differentiation
- Taylor mode Forward AD - for nth order AD
- Exact jacobian
Realtrait to constrain forf64andAD(for ODE)
- Numerical Analysis
- Lagrange interpolation
- Splines
- Cubic Spline
- Cubic Hermite Spline
- Estimate slope via Akima
- Estimate slope via Quadratic interpolation
- B-Spline
- Non-linear regression
- Gradient Descent
- Levenberg Marquardt
- Ordinary Differential Equation
- Trait based ODE solver (after
v0.36.0) - Explicit integrator
- Ralston's 3rd order
- Runge-Kutta 4th order
- Ralston's 4th order
- Runge-Kutta 5th order
- Embedded integrator
- Bogacki-Shampine 3(2)
- Runge-Kutta-Fehlberg 4(5)
- Dormand-Prince 5(4)
- Tsitouras 5(4)
- Implicit integrator
- Gauss-Legendre 4th order
- Trait based ODE solver (after
- Numerical Integration
- Newton-Cotes Quadrature
- Gauss-Legendre Quadrature (up to 30 order)
- Gauss-Kronrod Quadrature (Adaptive)
- G7K15, G10K21, G15K31, G20K41, G25K51, G30K61
- Gauss-Kronrod Quadrature (Relative tolerance)
- G7K15R, G10K21R, G15K31R, G20K41R, G25K51R, G30K61R
- Root Finding
- Trait based root finding (after
v0.37.0) - Bisection
- False Position
- Secant
- Newton
- Broyden
- Trait based root finding (after
- Statistics
- More easy random with
randcrate - Ordered Statistics
- Median
- Quantile (Matched with R quantile)
- Probability Distributions
- Bernoulli
- Uniform
- Binomial
- Normal
- Gamma
- Beta
- Student's-t
- Weighted Uniform
- RNG algorithms
- Acceptance Rejection
- Marsaglia Polar
- Ziggurat
- Wrapper for
rand-distcrate - Piecewise Rejection Sampling
- Confusion Matrix & Metrics
- More easy random with
- Special functions
- Wrapper for
puruspecrate (pure rust)
- Wrapper for
- Utils
- R-like macro & functions
- Matlab-like macro & functions
- Numpy-like macro & functions
- Julia-like macro & functions
- Plotting
- With
pyo3&matplotlib
- With
- DataFrame
- Support various types simultaneously
- Read & Write
csvfiles (csvfeature) - Read & Write
netcdffiles (ncfeature) - Read & Write
parquetfiles (parquetfeature)
6. Compatible with Mathematics
After 0.23.0, peroxide is compatible with mathematical structures.
Matrix, Vec<f64>, f64 are considered as inner product vector spaces.
And Matrix, Vec<f64> are linear operators - Vec<f64> to Vec<f64> and Vec<f64> to f64.
For future, peroxide will include more & more mathematical concepts. (But still practical.)
7. Written in Rust
Rust provides a strong type system, ownership concepts, borrowing rules, and other features that enable developers to write safe and efficient code. It also offers modern programming techniques like trait-based abstraction and convenient error handling. Peroxide is developed to take full advantage of these strengths of Rust.
The example code demonstrates how Peroxide can be used to simulate the Lorenz attractor and visualize the results. It showcases some of the powerful features provided by Rust, such as the ? operator for streamlined error handling and the ODEProblem trait for abstracting ODE problems.
use peroxide::fuga::*;
fn main() -> Result<(), Box<dyn Error>> {
let initial_conditions = vec![10f64, 1f64, 1f64];
let rkf45 = RKF45::new(1e-4, 0.9, 1e-6, 1e-2, 100);
let basic_ode_solver = BasicODESolver::new(rkf45);
let (_, y_vec) = basic_ode_solver.solve(
&Lorenz,
(0f64, 100f64),
1e-2,
&initial_conditions,
)?; // Error handling with `?` - can check constraint violation and etc.
let y_mat = py_matrix(y_vec);
let y0 = y_mat.col(0);
let y2 = y_mat.col(2);
// Simple but effective plotting
let mut plt = Plot2D::new();
plt
.set_domain(y0)
.insert_image(y2)
.set_xlabel(r"$y_0$")
.set_ylabel(r"$y_2$")
.set_style(PlotStyle::Nature)
.tight_layout()
.set_dpi(600)
.set_path("example_data/lorenz_rkf45.png")
.savefig()?;
Ok(())
}
struct Lorenz;
impl ODEProblem for Lorenz {
fn rhs(&self, t: f64, y: &[f64], dy: &mut [f64]) -> anyhow::Result<()> {
dy[0] = 10f64 * (y[1] - y[0]);
dy[1] = 28f64 * y[0] - y[1] - y[0] * y[2];
dy[2] = -8f64 / 3f64 * y[2] + y[0] * y[1];
Ok(())
}
}
Running the code produces the following visualization of the Lorenz attractor:
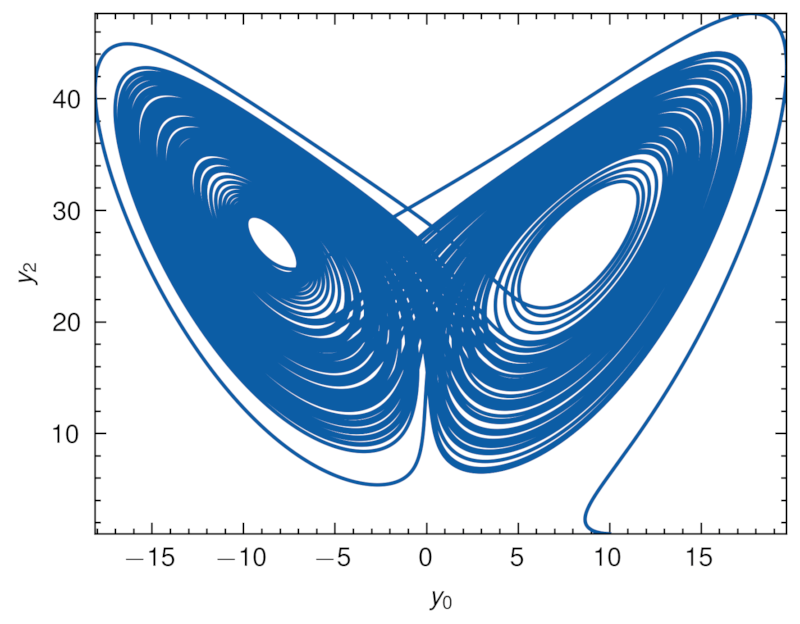
Peroxide strives to leverage the benefits of the Rust language while providing a user-friendly interface for numerical computing and scientific simulations.
How's that? Let me know if there's anything else you'd like me to improve!
Latest README version
Corresponding to 0.38.0
Pre-requisite
- For
O3feature - NeedOpenBLAS - For
plotfeature - Needmatplotliband optionalscienceplots(for publication quality) - For
ncfeature - Neednetcdf
Install
Basic Installation
cargo add peroxide
Featured Installation
cargo add peroxide --features "<FEATURES>"
Available Features
O3: Adds OpenBLAS supportplot: Enables plotting functionalitycomplex: Supports complex number operationsparallel: Enables parallel processing capabilitiesnc: Adds NetCDF support for DataFramecsv: Adds CSV support for DataFrameparquet: Adds Parquet support for DataFrameserde: Enables serialization/deserialization for Matrix and polynomial
Install Examples
Single feature installation:
cargo add peroxide --features "plot"
Multiple features installation:
cargo add peroxide --features "O3 plot nc csv parquet serde"
Useful tips for features
-
If you want to use QR, SVD, or Cholesky Decomposition, you should use the
O3feature. These decompositions are not implemented in thedefaultfeature. -
If you want to save your numerical results, consider using the
parquetorncfeatures, which correspond to theparquetandnetcdffile formats, respectively. These formats are much more efficient thancsvandjson. -
For plotting, it is recommended to use the
plotfeature. However, if you require more customization, you can use theparquetorncfeature to export your data in the parquet or netcdf format and then use Python to create the plots.-
To read parquet files in Python, you can use the
pandasandpyarrowlibraries. -
A template for Python code that works with netcdf files can be found in the Socialst repository.
-
Module Structure
- src
- lib.rs :
modandre-export - complex: For complex vector, matrix & integrals.
- mod.rs
- integrate.rs : Complex integral
- matrix.rs : Complex matrix
- vector.rs : Complex vector
- fuga : Fuga for controlling numerical algorithms.
- macros : Macro files
- julia_macro.rs : Julia like macro
- matlab_macro.rs : MATLAB like macro
- mod.rs
- r_macro.rs : R like macro
- ml : For machine learning (Beta)
- numerical : To do numerical things
- mod.rs
- eigen.rs : Eigenvalue, Eigenvector algorithm
- integral.rs : Numerical integration
- interp.rs : Interpolation
- newton.rs : Newton's Method
- ode.rs : Main ODE solver with various algorithms
- optimize.rs : Non-linear regression
- root.rs : Root finding
- spline.rs : Cubic spline, Cubic Hermite spline & B-Spline
- utils.rs : Utils to do numerical things (e.g. jacobian)
- prelude : Prelude for using simple
- mod.rs
- simpler.rs : Provides more simple api
- special : Special functions written in pure Rust (Wrapper of
puruspe)- mod.rs
- function.rs : Special functions
- statistics : Statistical Tools
- structure : Fundamental data structures
- mod.rs
- ad.rs : Automatic Differentation
- dataframe.rs : Dataframe
- matrix.rs : Matrix
- polynomial.rs : Polynomial
- sparse.rs : For sparse structure (Beta)
- vector.rs : Extra tools for
Vec<f64>
- traits
- mod.rs
- fp.rs : Functional programming toolbox
- general.rs : General algorithms
- math.rs : Mathematics
- matrix.rs : Matrix traits
- mutable.rs : Mutable toolbox
- num.rs : Number, Real and more operations
- pointer.rs : Matrix pointer and Vector pointer for convenience
- stable.rs : Implement nightly-only features in stable
- sugar.rs : Syntactic sugar for Vector
- util
- mod.rs
- api.rs : Matrix constructor for various language style
- low_level.rs : Low-level tools
- non_macro.rs : Primordial version of macros
- plot.rs : To draw plot (using
pyo3) - print.rs : To print conveniently
- useful.rs : Useful utils to implement library
- wrapper.rs : Wrapper for other crates (e.g. rand)
- writer.rs : More convenient write system
- lib.rs :
Documentation
Examples
-
In examples directory, there are some examples.
-
In tests directory, there are some useful tests.
-
More examples are in Peroxide Gallery.
Release Info
To see RELEASES.md
Contributes Guide
See CONTRIBUTES.md
LICENSE
Peroxide is licensed under dual licenses - Apache License 2.0 and MIT License.
TODO
To see TODO.md
Cite Peroxide
Hey there! If you're using Peroxide in your research or project, you're not required to cite us. But if you do, we'd be really grateful! 😊
To make citing Peroxide easy, we've created a DOI through Zenodo. Just click on this badge:
This will take you to the Zenodo page for Peroxide. At the bottom, you'll find the citation information in various formats like BibTeX, RIS, and APA.
So, if you want to acknowledge the work we've put into Peroxide, citing us would be a great way to do it! Thanks for considering it, we appreciate your support! 👍
Dependencies
~4–17MB
~284K SLoC