8 releases
| new 0.3.0 | May 8, 2025 |
|---|---|
| 0.2.0 | Apr 24, 2025 |
| 0.1.1 | Apr 3, 2025 |
| 0.1.0 | Mar 27, 2025 |
| 0.1.0-alpha.2 | Feb 27, 2025 |
#595 in Math
166 downloads per month
615KB
11K
SLoC
MosekCOModel is still an experimental project project. Use with caution,
expect rough corners and untested cases, and the API is subject to change
MosekCOModel
The MosekCOModel crate is a modeling package for building optimization models
with Mosek.rs. The Mosek.rs package is a
relatively thin interface in top of low-level MOSEK
optimizer C API, where MosekModel is an attempt to create an interface that
is more like the MOSEK Fusion modelling interface.
Published crates: https://crates.io/crates/mosekcomodel
Documentation for latest crates: https://docs.rs/mosekcomodel/latest/mosekcomodel/
Design principle
MosekModel allows building a model of the form
min/max c^t x + c_fix
such that Ax_b ∊ K_c
x ∊ K_x
That is affine expressions and conic domains of constraints and variables.
The MosekModel package provides functionality to build the linear expressions.
Simple conic example
Implementing the models
minimize y₁ + y₂ + y₃
such that
x₁ + x₂2 + 2.0 x₃ = 1.0
x₁,x₂,x₃ ≥ 0.0
and
(y₁,x₁,x₂) in C₃,
(y₂,y₃,x₃) in K₃
where C₃ and K₃ are respectively the quadratic and
rotated quadratic cone of size 3 defined as
C₃ = { z₁,z₂,z₃ : z₁ ≥ √(z₂² + z₃²) }
K₃ = { z₁,z₂,z₃ : 2 z1 z₂ ≥ z₃² }
This is the included model cqo1.rs:
extern crate mosekcomodel;
use mosekcomodel::*;
use mosekcomodel::expr::*;
fn main() {
let mut m = Model::new(Some("cqo1"));
let x = m.variable(Some("x"), greater_than(vec![0.0;3]));
let y = m.variable(Some("y"), 3);
// Create the aliases
// z1 = [ y[0],x[0],x[1] ]
// and z2 = [ y[1],y[2],x[2] ]
let z1 = Variable::vstack(&[&y.index(0..1), &x.index(0..2)]);
let z2 = Variable::vstack(&[&y.index(1..3), &x.index(2..3)]);
// Create the constraint
// x[0] + x[1] + 2.0 x[2] = 1.0
let aval = &[1.0, 1.0, 2.0];
let _ = m.constraint(Some("lc"), aval.dot(x.clone()), equal_to(1.0));
// Create the constraints
// z1 belongs to C_3
// z2 belongs to K_3
// where C_3 and K_3 are respectively the quadratic and
// rotated quadratic cone of size 3, i.e.
// z1[0] >= sqrt(z1[1]^2 + z1[2]^2)
// and 2.0 z2[0] z2[1] >= z2[2]^2
let qc1 = m.constraint(Some("qc1"), &z1, in_quadratic_cone(3));
let _qc2 = m.constraint(Some("qc2"), &z2, in_rotated_quadratic_cone(3));
// Set the objective function to (y[0] + y[1] + y[2])
m.objective(Some("obj"), Sense::Minimize, y.sum());
// Solve the problem
m.solve();
// Get the linear solution values
let solx = m.primal_solution(SolutionType::Default,&x);
let soly = m.primal_solution(SolutionType::Default,&y);
println!("x = {:?}", solx);
println!("y = {:?}", soly);
// Get primal and dual solution of qc1
let qc1lvl = m.primal_solution(SolutionType::Default,&qc1);
let qc1sn = m.dual_solution(SolutionType::Default,&qc1);
println!("qc1 levels = {:?}", qc1lvl);
println!("qc1 dual conic var levels = {:?}", qc1sn);
}
Compiling, testing, running
First, to build simply type
cargo build
Optionally, also pass the --release flag as the Debug build is significantly slower that the release build.
Running examples requires the MOSEK library to be available and a valid MOSEK license file. The simplest solution is to download and unpack the MOSEK distro from MOSEK Downloads, unpack the distro and set relevant environment variable:
- On MS Windows:
set PATH=C:\full\path\to\mosek\binaries;%PATH% - On Mac OSX:
export DYLD_LIBRARY_PATH=/full/path/to/mosek/binaries:$DYLD_LIBRARY_PATH - On Linux:
export LD_LIBRARY_PATH=/full/path/to/mosek/binaries:$LD_LIBRARY_PATH
To run tests, do
cargo test --all
A trial license can be obtained from MOSEK Trial license.
Demos
The project also contanis a set of graphical demos. These are in separate
sub-projects in examples/demos since they depend on a lot of external
libraries.
To run these, go to the sub-folder with demos
cd examples/demos
Then to run, say lowner-john-2d, do
cargo run --release -p lowner-john-2d
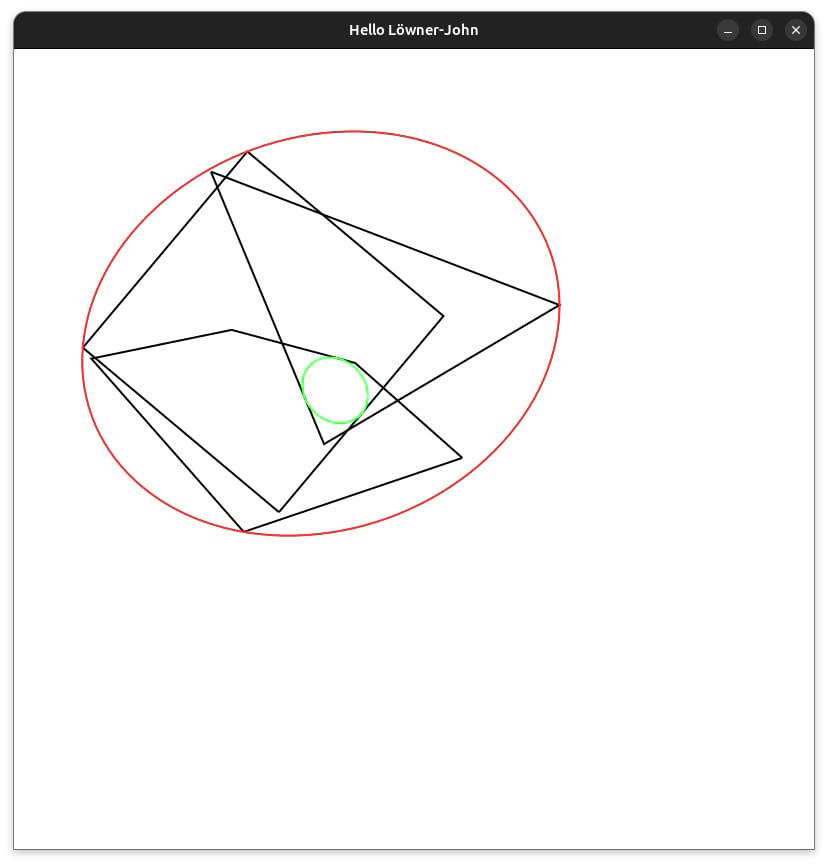
lowner-john-2d
For a set of moving, rotating polygons, computes the minimal bounding ellipsoid containing all polygons (or, in fact all corner points), and the maximum ellipsoid contained in the intersection (when the intersection is non-empty).
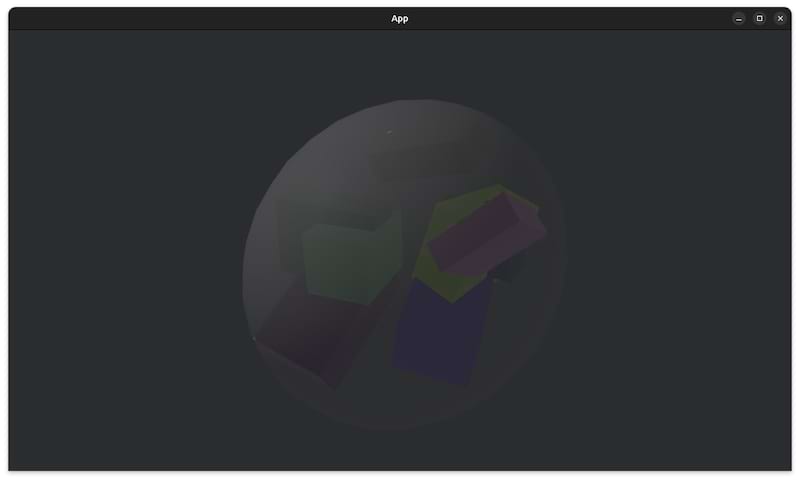
lowner-john-outer-3d
For a set of rotating and moving polyhedrons, compute the minimal bounding ellipsoid containing all polyhedrons (or their corner points).
ellipsoid-approximation
For a set of moving and rotating ellipses, compute the outer approximation (minimal ellipse containing all moving ellipses), and inner approximation (maximum ellipe contained in the intersection of all ellipses).
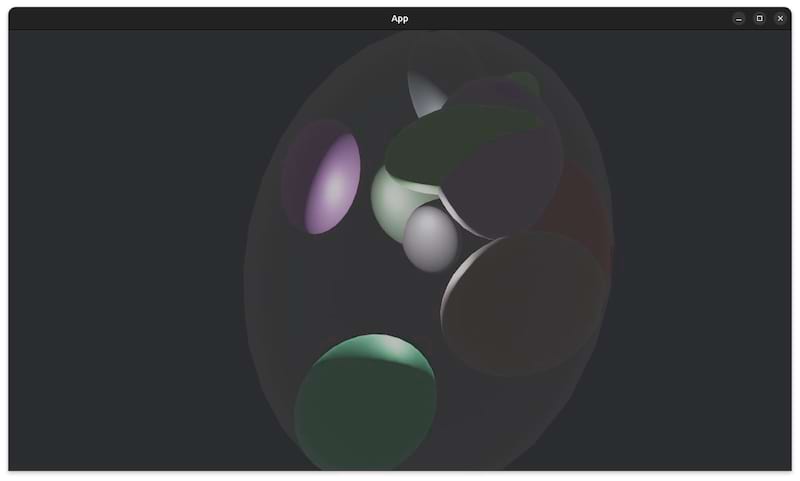
ellipsoid-approximation-3d
For a set of moving and rotating ellipsoids, compute the minimal bounding ellipsoid.

trigpoly
Simple visualization of trigonometric polynomial optimization.
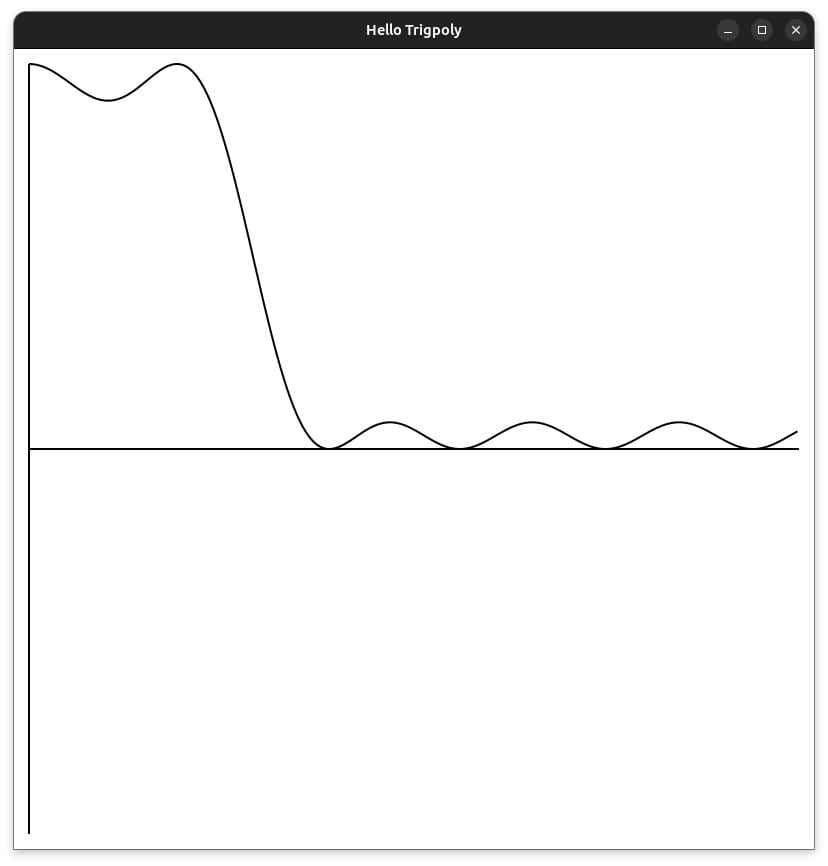
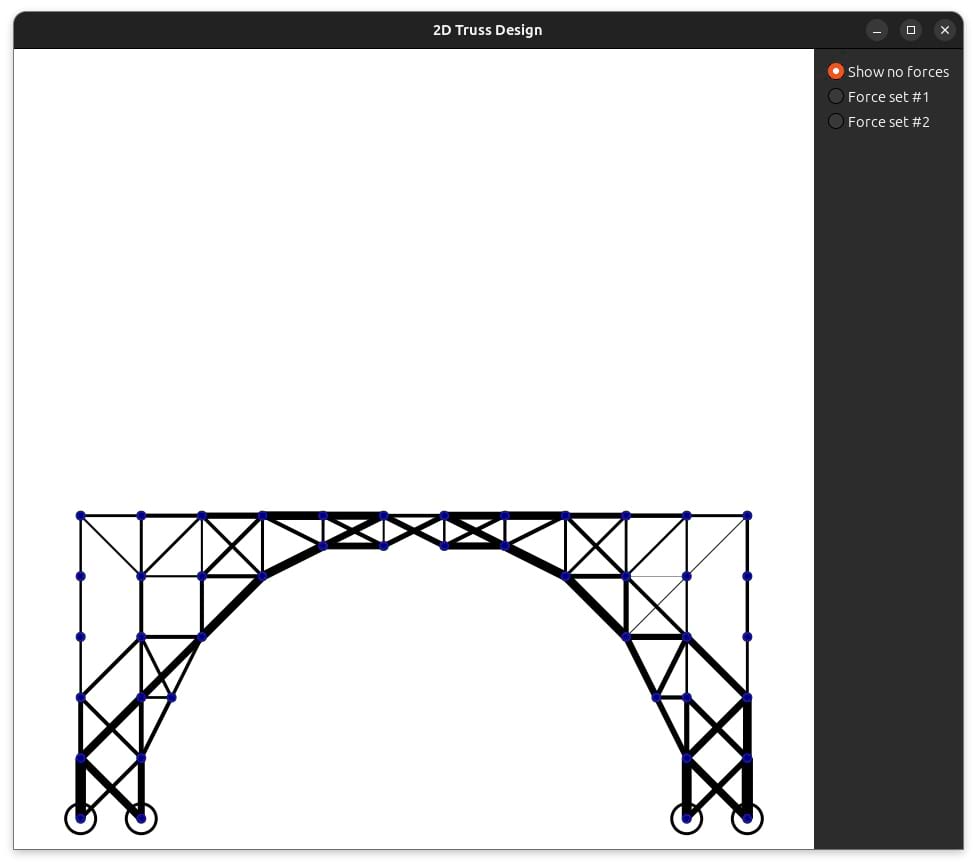
truss
Simple 2D truss design model assigning material to bars in a truss construction. This requires a data file, e.g.
cargo run --release -p truss -- truss/data/bridge.trs
Total Variation
Implements a simple image enhancement method as a optimization problem. Originally, the method was designed for use with a large scale first-order method, so this is mostly just a visual demonstration of an optimization result.
Run with --help to see further command line options.
cargo run --release -p total-variation
Traveling Salesman
Very simple implementation of the traveling salesman problem. Run with --help to see further command line options.
cargo run --release -p tsp
Dependencies
The amount of external dependencies is minimal.
- The crate directly depend in
itertoolsandmosek. - Some examples depend no
rand_distr - Benchmarking tests require
criterionandrand.
Dependencies
~3MB
~43K SLoC