95 releases (53 stable)
| 10.1.3 | May 26, 2024 |
|---|---|
| 9.3.1 | May 7, 2024 |
| 9.0.0 | Mar 9, 2024 |
| 8.0.1 | Feb 21, 2024 |
| 0.5.0 | Jul 20, 2021 |
#51 in No standard library
119 downloads per month
Used in 2 crates
(via four-bar)
80KB
1.5K
SLoC
EFD Rust Library
Elliptical Fourier Descriptor (EFD) implementation in Rust. This crate implements 1D/2D/3D EFD and its related functions.
This implementation is totally safe and supports no-std + alloc environment.
Keyword Alias:
- Elliptical Fourier Analysis (EFA)
- Elliptical Fourier Function (EFF)
Example of re-describing a new closed curve:
let curve = vec![
[0., 0.],
[1., 1.],
[2., 2.],
[3., 3.],
[2., 2.],
[1., 1.],
];
assert!(efd::util::valid_curve(&curve).is_some());
let described_curve = efd::Efd2::from_curve(curve, false).recon(20);
The harmonic number can be set with efd::Efd::from_curve_harmonic() method. The following figures show the reconstruction of a 2D closed curve with 1-8 harmonics.
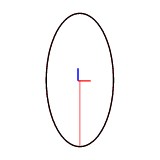
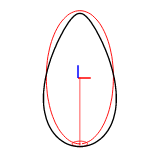
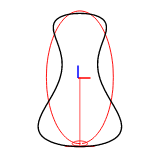
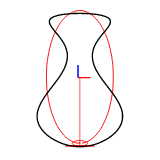
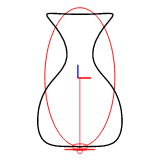
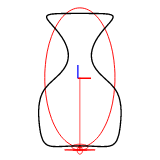
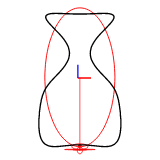
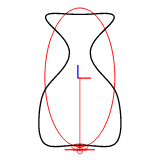
Example Images
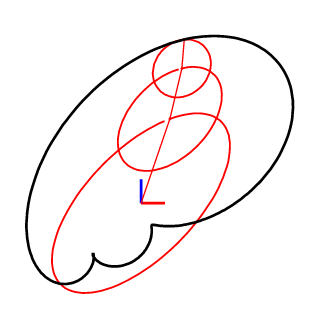
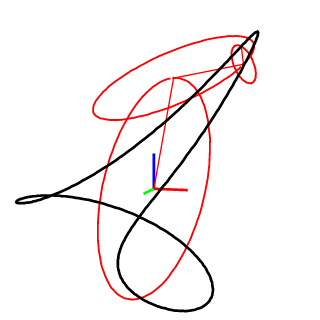
2D and 3D closed curve:
2D and 3D open curve:
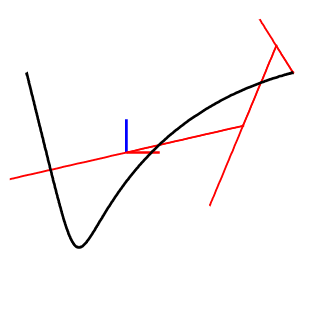
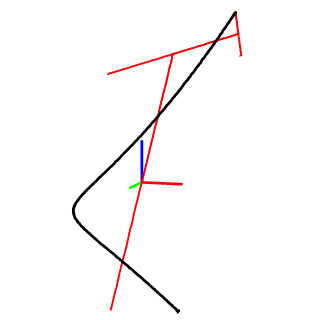
Posed EFD combined a curve with a pose (unit vectors) to describe the orientation of each point.
2D open curve and its full reconstruction:
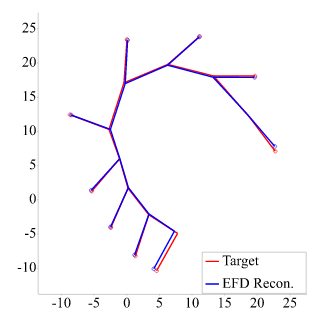
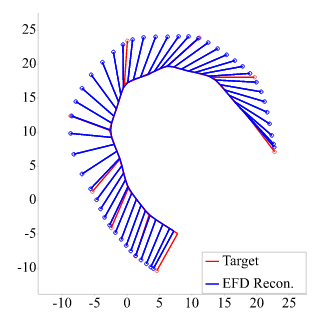
Citations
Original
- Kuhl, FP and Giardina, CR (1982). Elliptic Fourier features of a closed contour. Computer graphics and image processing, 18(3), 236-258. https://doi.org/10.1016/0146-664X(82)90034-X
My Applications
- Chang, Y., Chang, JL., Lee, JJ. (2024). Atlas-Based Path Synthesis of Planar Four-Bar Linkages Using Elliptical Fourier Descriptors. In: Okada, M. (eds) Advances in Mechanism and Machine Science. IFToMM WC 2023. Mechanisms and Machine Science, vol 149. Springer, Cham. https://doi.org/10.1007/978-3-031-45709-8_20
- Chang, Y., Chang, JL. & Lee, JJ. Path Synthesis of Planar Four-bar Linkages for Closed and Open Curves Using Elliptical Fourier Descriptors. J Mech Sci Technol (2024). http://doi.org/10.1007/s12206-024-0436-y
Dependencies
~4.5MB
~91K SLoC