11 releases (6 stable)
| 1.2.2 | Mar 22, 2025 |
|---|---|
| 1.1.3 | Feb 26, 2025 |
| 1.1.0 | Sep 2, 2024 |
| 0.6.0 | Aug 26, 2024 |
#187 in Algorithms
35 downloads per month
1.5MB
12K
SLoC
Optirustic
Optirustic is a framework written in Rust that provides algorithms and analysis tool to solve multi-objective problems using multi-objective evolutionary algorithms (MOEAs). It allows you to:
- define minimisation and maximisation problems with custom objective functions;
- define constraint and unconstrained variables (real, integer, boolean or choice);
- use multi-thread to evaluate objectives and constraints on population with many individuals
- export the population history as JSON and resume its evolution from file
- generate charts with the dedicated Python package
The library comes with the following
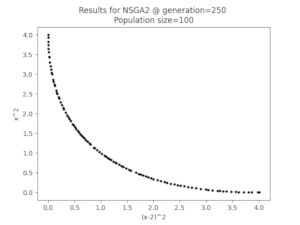
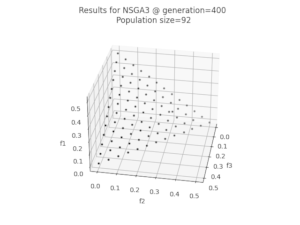
algorithms: NSGA2,
NSGA3 and
AdaptiveNSGA3.
The API documentation is available on docs.rs. Examples showcasing this library's features are available in the examples folder of this repository.
Installing Optirustic
Optirustic is available on crates.io. The recommended way to use it is to add a line into your Cargo.toml:
[dependencies]
optirustic = "*"
Example
Problem definition
In this example, we are going to solve the Schaffer’s problem with the NSGA2 algorithm.
The problem aims to minimise the following 2 objectives:
- f1(x) = x2
- f2(x) = (x - 2)2
The problem has 1 variable (x) bounded to -1000 and 1000. The optional solution is expected
to lie in the [0; 2] range.
Problem implementation
The problem is implemented below using the SCHProblem struct. When an algorithm runs,
it first generates a set of potential solutions for the problem variables (in this case x). It
then calculates the objectives (f1(x) and f2(x)) in the Evaluator
trait exposed by this library.
#[derive(Debug)]
pub struct SCHProblem;
impl SCHProblem {
/// Create the problem for the optimisation.
pub fn create() -> Result<Problem, OError> {
// define the objectives
let objectives = vec![
Objective::new("x^2", ObjectiveDirection::Minimise),
Objective::new("(x-2)^2", ObjectiveDirection::Minimise),
];
// define the variable
let variables = vec![VariableType::Real(BoundedNumber::new(
"x", -1000.0, 1000.0,
)?)];
// the problem has no constraints
let constraints = None;
let e = Box::new(SCHProblem);
Problem::new(objectives, variables, constraints, e)
}
/// The first objective function
pub fn f1(x: f64) -> f64 {
x.powi(2)
}
/// The second objective function
pub fn f2(x: f64) -> f64 {
(x - 2.0).powi(2)
}
}
// Implement the function to evaluate the objectives and constraints. The `evaluate`
// function below receives the individuals which contain the variables/solutions `x`
// proposed by the algorithm. The function must return the evaluated objectives and
// constraints in the `EvaluationResult` struct.
impl Evaluator for SCHProblem {
fn evaluate(&self, i: &Individual) -> Result<EvaluationResult, Box<dyn Error>> {
let x = i.get_variable_value("x")?.as_real()?;
let mut objectives = HashMap::new();
objectives.insert("x^2".to_string(), SCHProblem::f1(x));
objectives.insert("(x-2)^2".to_string(), SCHProblem::f2(x));
Ok(EvaluationResult {
constraints: None,
objectives,
})
}
}
Setup and run the genetic algorithm
The code below set up the NSGA2 algorithm with 100 individuals and will
stop when 250 population generations are reached.
...
fn main() -> Result<(), Box<dyn Error>> {
// Setup the NSGA2 algorithm
let args = NSGA2Arg {
// use 100 individuals and stop the algorithm at 250 generations
number_of_individuals: 100,
stopping_condition: StoppingConditionType::MaxGeneration(MaxGeneration(250)),
// use default options for the SBX and PM operators
crossover_operator_options: None,
mutation_operator_options: None,
// no need to evaluate the objective in parallel
parallel: Some(false),
// do not export intermediate solutions
export_history: None,
resume_from_file: None,
// to reproduce results
seed: Some(10),
};
let mut algo = NSGA2::new(problem, args)?;
// run the algorithm
algo.run()?;
// Export serialised results at last generation
algo.save_to_json(&PathBuf::from("."), Some("SCH_2obj"))?;
Ok(())
}
The full example is available in the examples folder of this repository and can be run using
cargo run --example nsga2_sch --release
This is the serialised data exported by the algorithm: SCH_2obj_NSGA2_gen250.json and these are the plotted solutions:
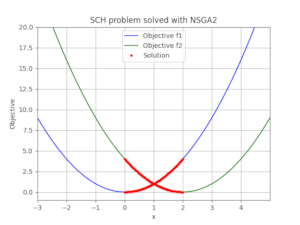
Plotting and inspecting data
With the library, you can set
the export_history
option, to export serialised results as JSON files as the algorithm evolves, or
call save_to_json
to export the results at the last population evolution.
This crate comes with a companion Python package to inspect the results
and easily plot the Pareto front or the algorithm convergence. This is how all the charts within
this README file were generated. Have a look at the py file in the example folder.
License
This project is licensed under the terms of the MIT license.
Dependencies
~7–11MB
~217K SLoC