3 releases (breaking)
| 0.3.0 | Jun 25, 2024 |
|---|---|
| 0.2.0 | Jun 10, 2024 |
| 0.1.0 | Mar 12, 2024 |
#1381 in Algorithms
149 downloads per month
84KB
2K
SLoC
Modular Decomposition
A library to compute the modular decomposition of a simple, undirected graph.
A node set M is a module if every node has the same neighborhood outside M. The set of all nodes V and the sets with a single node {u} are trivial modules.
The modular decomposition algorithm in this library has a O(n + m log n) running time and is based on [HPV99] and [CHM02]. Although linear time algorithms exists, they perform worse in comparison.
Examples
The smallest prime graph is the path graph on 4 nodes.
use petgraph::graph::UnGraph;
use modular_decomposition::{ModuleKind, modular_decomposition};
// a path graph with 4 nodes
let graph = UnGraph::<(), ()>::from_edges([(0, 1), (1, 2), (2, 3)]);
let md = modular_decomposition(&graph)?;
assert_eq!(md.module_kind(md.root()), Some(&ModuleKind::Prime));
Determining whether a graph is a cograph.
use petgraph::graph::UnGraph;
use modular_decomposition::{ModuleKind, modular_decomposition};
// a complete graph with 3 nodes
let graph = UnGraph::<(), ()>::from_edges([(0, 1), (0, 2), (1, 2)]);
let md = modular_decomposition(&graph)?;
// a graph is a cograph exactly if none of its modules is prime
let is_cograph = md.module_kinds().all(|kind| *kind != ModuleKind::Prime);
assert!(is_cograph);
// we can also use the method `is_cograph`
assert!(md.is_cograph());
Iterating over twins, true twins or false twins.
use petgraph::graph::{NodeIndex, UnGraph};
use modular_decomposition::modular_decomposition;
let normalize = |sets: &[Vec<NodeIndex>]| -> Vec<Vec<usize>> {
let mut sets: Vec<Vec<usize>> = sets.iter().map(|nodes| nodes.iter().map(|node| node.index()).collect()).collect();
sets.iter_mut().for_each(|nodes| nodes.sort());
sets.sort();
sets
};
// a K_2 + 2 K_1
let graph = UnGraph::<(), ()>::from_edges([(2, 3)]);
let md = modular_decomposition(&graph)?;
let twins: Vec<_> = md.twins().collect();
assert_eq!(normalize(&twins), [[0, 1], [2, 3]]);
let true_twins: Vec<_> = md.true_twins().collect();
assert_eq!(normalize(&true_twins), [[2, 3]]);
let false_twins: Vec<_> = md.false_twins().collect();
assert_eq!(normalize(&false_twins), [[0, 1]]);
Walking the modular decomposition tree in DFS order.
use petgraph::graph::{NodeIndex, UnGraph};
use modular_decomposition::modular_decomposition;
// some graph
let graph = UnGraph::<(), ()>::from_edges([(2, 3), (3, 4)]);
let md = modular_decomposition(&graph)?;
let mut stack = vec![md.root()];
while let Some(module) = stack.pop() {
stack.extend(md.children(module));
// do something with module
// ...
}
Generics
The algorithm is implemented for structs that implement the petgraph
traits NodeCompactIndexable, IntoNeighbors, and GraphProp<EdgeType = Undirected>.
Evaluation
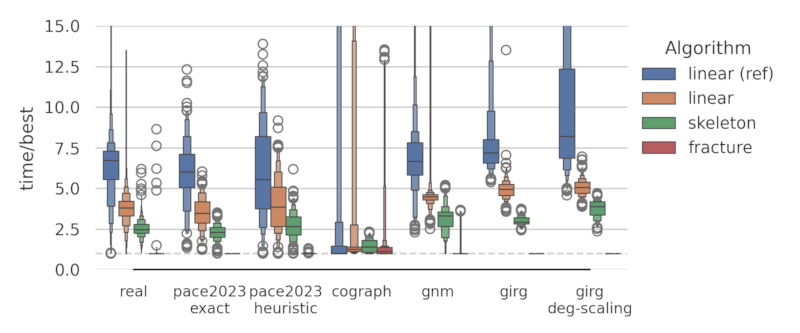
As part of a thesis, we evaluated four implementations of modular decomposition algorithms.
The fracture algorithm performs best and is provided in this library. For more information see
the repository.
Citing
Jonas Spinner. "A Practical Evaluation of Modular Decomposition Algorithms". https://doi.org/10.5445/IR/1000170363
@mastersthesis{Spinner2024,
doi = {10.5445/IR/1000170363},
url = {https://doi.org/10.5445/IR/1000170363},
title = {A Practical Evaluation of Modular Decomposition Algorithms},
author = {Spinner, Jonas},
year = {2024},
publisher = {{Karlsruher Institut für Technologie (KIT)}},
school = {Karlsruher Institut für Technologie (KIT)},
language = {english}
}
Dependencies
~2.5MB
~36K SLoC