8 stable releases
| 1.1.3 | Oct 28, 2020 |
|---|---|
| 1.1.1 |
|
| 1.1.0 | Oct 22, 2020 |
| 1.0.4 | Oct 18, 2020 |
| 1.0.2 | Oct 17, 2020 |
#2011 in Math
26 downloads per month
14KB
229 lines
makima_spline
A implementation of the modified akima interpolation
+ linear extrapolation
+ 1., 2., and 3. order derivatives
+ bicubic interpolation as a feature
HowTo
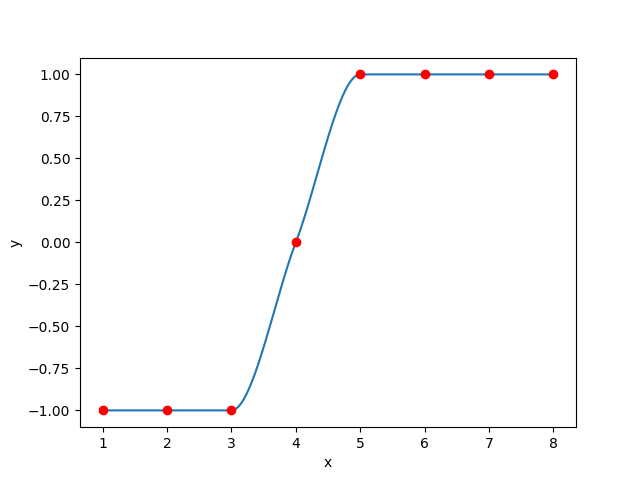
use makima_spline::Spline;
your data is in some format
let x = vec![1., 2., 3., 4., 5., 6., 7., 8.];
let y = vec![-1., -1., -1., 0.0, 1., 1., 1., 1.];
convert to the type used by the spline Vec<(f64, f64)>
let points = makima_spline::vec_to_points(&x, &y);
build the spline from the data-points
let spline = Spline::from_vec(points);
To sample do this:
let y = spline.sample(x);
2d interpolation
Based on the bicubic crate it is possible to interpolate in two dimensions.
Create points
let x = vec![-1.0, 0.0, 2.0];
let y = vec![-0.0, 1.0];
let f = vec![5.0, 4.0, 5.0, 1.0, 1.0, 1.0];
construct Bicubic Struct
let bci = makima_spline::n_dimensional::bicubic_from_grid(&x, &y, &f);
The submodule is called n_dimensional in case higher dimensions will be supported in the future, but currently there is only 2d interpolation