9 unstable releases (4 breaking)
| 0.6.2 | Mar 28, 2025 |
|---|---|
| 0.6.1 | Mar 26, 2025 |
| 0.5.1 | Mar 26, 2025 |
| 0.5.0 | Aug 16, 2024 |
| 0.2.0 | Mar 24, 2024 |
#319 in Math
524 downloads per month
33KB
433 lines
lazyivy
lazyivy is a Rust crate that provides tools to solve initial value problems of
the form dY/dt = F(t, Y) using Runge-Kutta methods, where Y is a vector
and t is a scalar.
The algorithms are implemented using the struct RungeKutta, that implements
Iterator. The following Runge-Kutta methods are supported.
- Euler 1
- Ralston 2
- Huen-Euler 2(1)
- Bogacki-Shampine 3(2)
- Fehlberg 4(5)
- Dormand-Prince 5(4)
(p is the order of the method and (p*) is the order of the embedded
error estimator, if it is present.)
Lazy Integration
RungeKutta implements the Iterator trait. Each .next() call advances the
iteration to the next Runge-Kutta step and returns a tuple (t, Y), where
t is the dependent variable and Y is Array1<f64>.
Note that each Runge-Kutta step contains s number of internal stages.
Using lazyivy, there is no way at present to access the integration values for
these inner stages. The .next() call returns the final result for each step,
summed over all stages.
The lazy implementation of Runge-Kutta means that you can consume the iterator
in different ways. For e.g., you can use .last() to keep only the final
result, .collect() to gather the state at all steps, .map() to chain the
iterator with another, etc. You may also choose to use it in a for loop and
implement you own logic for modifying the step-size or customizing the stop
condition.
Usage
After adding lazyivy to Cargo.toml, create an initial value problem using
the provided builder. Here is an example
showing how to solve the Brusselator.
\frac{d}{dt} \left[ \begin{array}{c}
y_1 \\ y_2 \end{array}\right] = \left[\begin{array}{c}1 - y_1^2 y_2 - 4 y_1
\\ 3y_1 - y_1^2 y_2 \end{array} \right]
use lazyivy::{RungeKutta, RungeKuttaMethod};
use ndarray::{array, ArrayView1, ArrayViewMut1};
fn brusselator(_t: &f64, y: ArrayView1<f64>, mut result: ArrayViewMut1<f64>) {
result[0] = 1. + y[0].powi(2) * y[1] - 4. * y[0];
result[1] = 3. * y[0] - y[0].powi(2) * y[1];
}
fn main() {
let t0: f64 = 0.;
let y0 = array![1.5, 3.];
let absolute_tol = array![1.0e-4, 1.0e-4];
let relative_tol = array![1.0e-4, 1.0e-4];
// Instantiate a integrator for an ODE system with adaptive step-size
// Runge-Kutta. The `builder` method takes in as argument the evaluation
// function and the predicate function (that determines when to stop). You
// need to call `build()` to consume the builder and return a `RungeKutta`
// struct.
let mut integrator = RungeKutta::builder(brusselator, |t, _| *t > 40.)
.initial_condition(t0, y0)
.initial_step_size(0.025)
.method(RungeKuttaMethod::DormandPrince, true) // `true` for adaptive step-size
.tolerances(absolute_tol, relative_tol)
.set_max_step_size(0.25)
.build()
.unwrap();
// For adaptive algorithms, you can use this to improve the initial guess
// for the step size.
integrator.set_step_size(&integrator.guess_initial_step());
// Perform the iterations and print each state.
for item in integrator {
println!("{:?}", item); // Prints (t, array[y1, y2]) for each step.
}
}
The result when plotted looks like this,
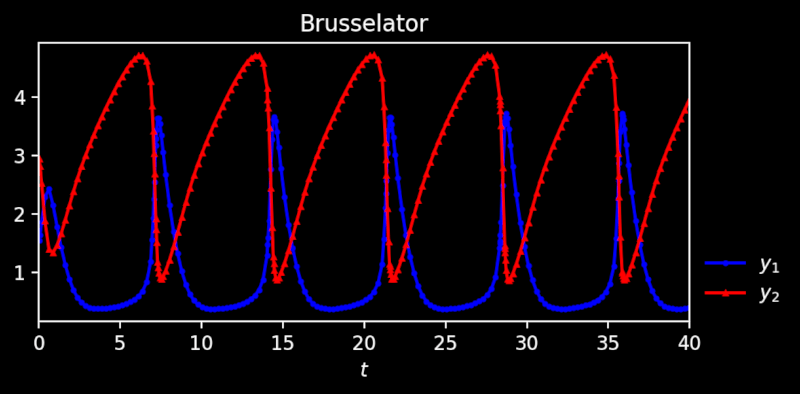
Likewise, you can do the same for other problems, e.g. for the Lorenz attractor, define the evaluation function -
fn lorentz_attractor(_t: &f64, y: ArrayView1<f64>, mut result: ArrayViewMut1<f64>) {
result[0] = 10. * (y[1] - y[0]);
result[1] = y[0] * (28. - y[2]) - y[1];
result[2] = y[0] * y[1] - 8. / 3. * y[2];
}
You can also use closures to capture the environment and wrap your evaluation. That is, if you have a function -
fn lorentz_attractor(
x: f64,
y: f64,
z: f64,
sigma: f64,
beta: f64,
rho: f64
) -> Array1<f64> {
array![
sigma * (y - x),
x * (rho - z) - y,
x * y - beta * z,
]
}
you cannot pass this to RungeKutta::builder() directly. But you can wrap this
into a closure. E.g.,
let sigma = 10.;
let beta = 8. / 3.;
let rho: 28.;
let eval_closure = |_t, y, result| { // here result is mut
// Closure captures the environment and wraps the function signature
result = lorentz_attractor(y[0], y[1], y[2], sigma, beta, rho);
};
let integrator = RungeKutta::builder(eval_closure, |t, _| *t > 20.)
... // other parameters
.build();
This works because closures that do not modify their environments can coerce to
Fn. Hence, this pattern will not work for closures that mutate their
environments. In general, you can use any evaluation function and stop condition,
but they must be Fn(&f64, ArrayView1<f64>, ArrayViewMut1<f64>) and
Fn(&f64, ArrayView1<f64>) -> bool, respectively.
Here is a plot showing the Lorenz attractor result.
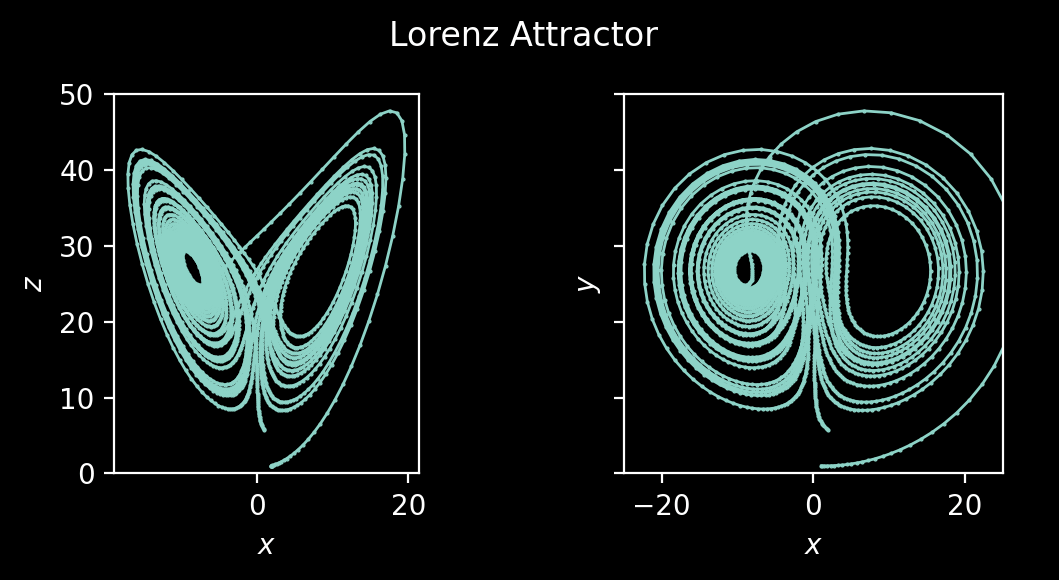
Dependencies
~1.5–2MB
~41K SLoC