icao-wgs84

A library for performing geometric calculations on the WGS84 ellipsoid, see Figure 1.

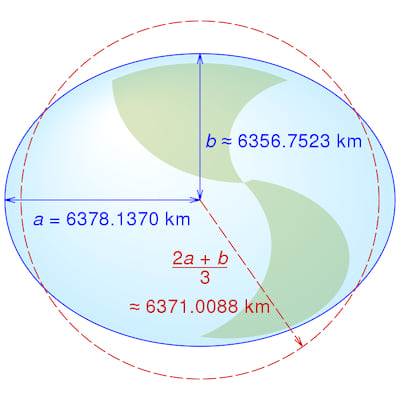
Figure 1 The WGS84 Ellipsoid (not to scale)

WGS84 has become the de facto standard for satellite navigation since its adoption by the Navstar Global Positioning System (GPS) and US president Ronald Reagan's 1983 decision to make GPS available for civilian use after airliner KAL 007 was shot down by Soviet interceptor aircraft when it strayed into prohibited airspace due to navigational errors.

This library uses the WGS84 primary parameters defined in Tab. 3-1 of the ICAO WGS 84 Implementation Manual.

Geodesic navigation

The shortest path between two points on the surface of an ellipsoid is a geodesic - the equivalent of straight line segments in planar geometry or great circles on the surface of a sphere, see Figure 2.

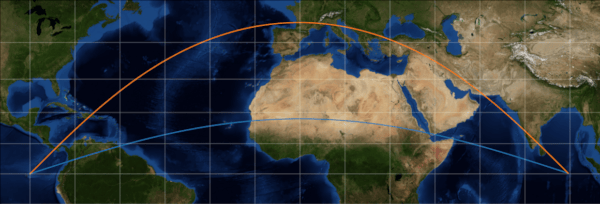
Figure 2 A geodesic between points A and B

Karney(2013) solves geodesic problems by mapping a geodesic onto the auxiliary sphere and then solving the corresponding problem in great-circle navigation. Karney solves geodesic intersection and point-to-line problems using a planar gnomonic projection.

Baselga and Martinez-Llario(2017) solve geodesic intersection and point-to-line problems by using the correspondence between geodesics on an ellipsoid and great-circles on the auxiliary sphere.

Nick Korbey and I Barker and Korbey(2019) developed Baselga and Martinez-Llario's algorithms by using vectors to solve geodesic intersection and point-to-line problems on the auxiliary sphere.

This library uses the correspondence between geodesics on an ellipsoid and great-circles on the auxiliary sphere together with 3D vectors to calculate:

• the initial azimuth and length of a geodesic between two positions;
• the along track distance and across track distance of a position relative to a geodesic;
• and the intersection of a pair of geodesics.

Examples

Calculate geodesic initial azimuth and length

Calculate the initial azimuth (a.k.a bearing) in degrees and distance in Nautical Miles between two positions.

use icao_wgs84::*;

let wgs84_ellipsoid = Ellipsoid::wgs84();

let istanbul = LatLong::new(Degrees(42.0), Degrees(29.0));
let washington = LatLong::new(Degrees(39.0), Degrees(-77.0));
let (azimuth, length) = calculate_azimuth_and_geodesic_length(&istanbul, &washington, &wgs84_ellipsoid);

let azimuth_degrees = Degrees::from(azimuth);
println!("Istanbul-Washington initial azimuth: {:?}", azimuth_degrees.0);

let distance_nm = NauticalMiles::from(length);
println!("Istanbul-Washington distance: {:?}", distance_nm);

Calculate along track and across track distances

Create a Geodesic between two positions and then calculate the along track and across track distances of a third position relative to the Geodesic.

The example is based on this reply from C. F. F. Karney : https://sourceforge.net/p/geographiclib/discussion/1026621/thread/21aaff9f/#8a93.
The expected latitude and longitude are from Karney's reply:

Final result 54.92853149711691 -21.93729106604878

Note: the across track distance (xtd) is negative because Reyjavik is on the right hand side of the Geodesic.
Across track distances are:

• positive for positions to the left of the Geodesic,
• negative for positions to the right of the Geodesic
• and zero for positions within the precision of the Geodesic.

use icao_wgs84::*;
use angle_sc::is_within_tolerance;

let wgs84_ellipsoid = Ellipsoid::wgs84();

let istanbul = LatLong::new(Degrees(42.0), Degrees(29.0));
let washington = LatLong::new(Degrees(39.0), Degrees(-77.0));
let g1 = Geodesic::between_positions(&istanbul, &washington, &wgs84_ellipsoid);

let azimuth_degrees = Degrees::from(g1.azimuth(Metres(0.0)));
println!("Istanbul-Washington initial azimuth: {:?}", azimuth_degrees.0);

let distance_nm = NauticalMiles::from(g1.length());
println!("Istanbul-Washington distance: {:?}", distance_nm);

let reyjavik = LatLong::new(Degrees(64.0), Degrees(-22.0));

// Calculate geodesic along track and across track distances to 1mm precision.
let (atd, xtd, iterations) = g1.calculate_atd_and_xtd(&reyjavik, Metres(1e-3));
assert!(is_within_tolerance(3928788.572, atd.0, 1e-3));
assert!(is_within_tolerance(-1010585.9988368, xtd.0, 1e-3));
println!("calculate_atd_and_xtd iterations: {:?}", iterations);

let position = g1.lat_long(atd);
assert!(is_within_tolerance(
    54.92853149711691,
    Degrees::from(position.lat()).0,
    128.0 * core::f64::EPSILON
));
assert!(is_within_tolerance(
    -21.93729106604878,
    Degrees::from(position.lon()).0,
    2048.0 * core::f64::EPSILON
));

Also Note: the example uses 1mm precision to match Karney's result.
In practice, precision should be determined from position accuracy.
Higher precision requires more iterations and therefore takes longer to calculate the result.

Calculate geodesic intersection

Create two Geodesics, each between two positions and then calculate the distances from the geodesic start points to their intersection point.

The example is based on this reply from C. F. F. Karney : https://sourceforge.net/p/geographiclib/discussion/1026621/thread/21aaff9f/#fe0a
The expected latitude and longitude are from Karney's reply:

Final result 54.7170296089477 -14.56385574430775

Note: Karney's solution requires all 4 positions to be in the same hemisphere centered at the intersection point.
This solution does not have that requirement.

use icao_wgs84::*;
use angle_sc::is_within_tolerance;

let wgs84_ellipsoid = Ellipsoid::wgs84();

let istanbul = LatLong::new(Degrees(42.0), Degrees(29.0));
let washington = LatLong::new(Degrees(39.0), Degrees(-77.0));
let reyjavik = LatLong::new(Degrees(64.0), Degrees(-22.0));
let accra = LatLong::new(Degrees(6.0), Degrees(0.0));

let g1 = Geodesic::from((&istanbul, &washington, &wgs84_ellipsoid));
let g2 = Geodesic::from((&reyjavik, &accra, &wgs84_ellipsoid));

// Calculate distances from the geodesic start points to the intersection point to 1mm precision.
let (distance1, _distance2, iterations) =
    calculate_intersection_distances(&g1, &g2, Metres(1e-3));
println!(
    "calculate_intersection_distances iterations: {:?}",
    iterations
);

// Get the intersection point position
let lat_lon = g1.aux_lat_long(distance1);
assert!(is_within_tolerance(54.7170296089477, lat_lon.lat().0, 1e-6));
assert!(is_within_tolerance(-14.56385574430775, lat_lon.lon().0, 1e-6));

Design

The library is based on Charles Karney's GeographicLib library. Like GeographicLib, it models geodesic paths as great circles on the surface of an auxiliary sphere. However, it also uses vectors to calculate along track distances, across track distances and intersections between geodesics.

The library depends upon the following crates:

• angle-sc - to define Angle, Degrees and Radians and perform trigonometric calculations;
• unit-sphere - to define LatLong and perform great-circle and vector calculations.
• icao_units - to define Metres and NauticalMiles and perform conversions between them.

Figure 3 Class Diagram

The library is declared no_std so it can be used in embedded applications.

Test

The integration test uses Charles Karney's Test data for geodesics to verify geodesic azimuth and distance calculations between positions on the WGS84 ellipsoid. Run the tests using:

cargo test -- --ignored

Contribution

If you want to contribute through code or documentation, the Contributing guide is the best place to start. If you have any questions, please feel free to ask. Just please abide by our Code of Conduct.

License

icao-wgs84 is provided under a MIT license, see LICENSE.