3 releases
| 0.4.2 | Apr 29, 2019 |
|---|---|
| 0.4.1 | Apr 29, 2019 |
| 0.3.2 |
|
| 0.2.0 |
|
| 0.1.0 |
|
#14 in #nearest
24 downloads per month
80KB
1.5K
SLoC
hwt
Hamming Weight Tree from the paper Online Nearest Neighbor Search in Hamming Space
To understand how the data structure works, please see the docs.
Benchmarks
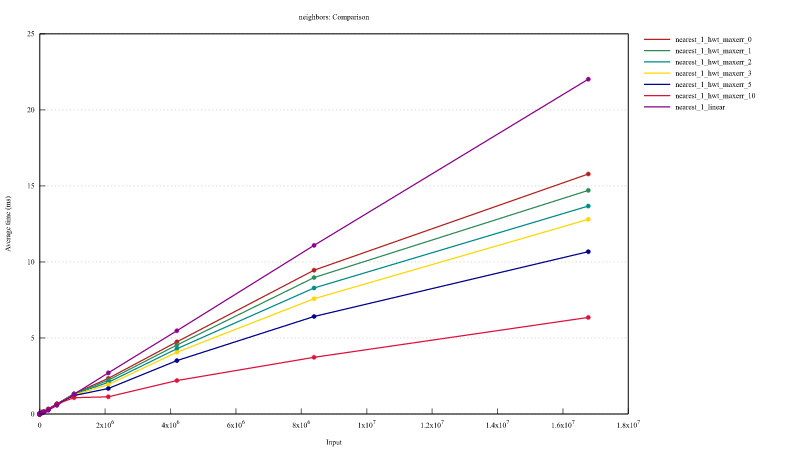
Most recent benchmark for 1-NN:
You can find benchmark output here.
If you would like to run the benchmarks yourself, just run cargo bench at the command line. I recommend using RUSTFLAGS='-C target-cpu=native' cargo bench instead since both linear search and this tree are both significantly faster when using modern instructions.
lib.rs:
Hwt
The Hamming Weight Tree was originally implemented in the paper "Online Nearest Neighbor Search in Hamming Space" by Sepehr Eghbali, Hassan Ashtiani, and Ladan Tahvildari. This is an attempt to improve on the performance and encapsulate the implementation in a Rust crate for easy consumption.
Here is how we would like to think about a number visually, in terms of a binary tree of its substring hamming weights:
5
3 2
2 1 1 1
1 1 0 1 1 0 0 1
Let B be the log2 of the width of the number. In this case B = 3,
since 2^3 = 8.
Let L be the level of the hamming tree. The hamming
weight of the whole number is the root and is L = 0.
Let N be the index at the level L of the substring weight in question.
Let W be a weight of the substring N at level L.
Let MAX be the side max of the hamming tree. MAX = min(W, 2^(B - L - 1)).
This is the maximum number of ones that either side of a substring can
have.
Let MIN be the side min of the hamming tree. MIN = W - MAX.
This is the minimum number of ones that either side of a substring can
have.
Every time we encounter a weight W in the tree then the next two
substrings can vary from [MIN, MAX] to [MAX, MIN] for a total of
A + 1 possibilities. Therefore we can also view the tree like this:
5 [1-4] 2
3 2 [1-2] [0-2] 1 1
2 1 1 1 [1-1] [0-1] [0-1] [0-1] 0 0 1 0
1 1 0 1 1 0 0 1
On the left we have the actual tree. In the middle we have the
possible values for the left branch. On the right we have the index
of the left branch chosen, which is calculated by subtracting the left
substring weight by MIN.
To compute the index for L we must iteratively multiply an accumulator
by MAX - MIN + 1 of the current substring N, add the substring's index
from the tree, then shift the number over by the substring width to get
N + 1.
To do the reverse, we must mod the accumulator by the multiplication of
all lower substring MAX - MIN + 1 to get the index of that substring
and then divide by the MAX - MIN + 1 of the current substring.
Do this iteratively to produce all weights for a given index.
We should avoid computing the weights from the index more than once
per operation if possible because it is costly due to modulo and division.
Searching
To limit the search space, we depend on the fact that the sum of the
absolute differences of hamming weights of substrings cannot exceed
the sum of the hamming distances of substrings. This means if the
sum of the absolute differences in hamming weights between the
bucket index's implicit weights at any given level of the tree
exceeds radius then we know it is impossible for any results to be
found in that branch of the tree. This allows us to filter what we
search to be only nodes that could theoretically match.
For the top level, its clear to scan (weight-radius..=weight+radius).
This is because results cannot be found outside where the weight differs
by more than radius. For the levels below that it becomes more
complicated to search the bucket. To do so, let us consider the case of
L = 0 (the 0th level starts after looking up the bucket for the overall
hamming weight).
Lets say we have a 128-bit feature with this tree of hamming weights:
5
3 2
If we want to search for things in radius <= 1 then at the top level we
search 4..6. Let us consider what happens when we then try to search the
bucket found at index 4. At this point we have a situation where the left
side could vary in 0..=4, since we have a 128-bit number, each half can
easily fit 4 ones. However, we dont need to search all of these
possibilites.
If the left side were to have a weight of 1 then the right
side would have a weight of 3. Remember "the sum of the absolute
differences of hamming weights of substrings cannot exceed the sum of
the hamming distances of substrings." If we look at our search point, we
find that the sum of the differences is abs(3 - 1) + abs(2 - 3) = 3.
This is greater than our search radius of 1, therefore it is impossible
to find a number with a hamming distance within the radius there.
Now consider what happens if we go to a weight of 2 on the left side.
In this case we have 2 bits on the right side. The sum of the differences
is abs(3 - 2) + abs(2 - 2) = 1. This is equal to our search radius and
therefore it is possible to find a match in that bucket.
In conclusion, we need to iterate in 2..=3. This has limited the
possibilities greatly. However, we need to know how to derive this range.
What we are going to find specifically is the way to derive the range of
the left substring weight (not the actual bucket index) that allows just
that substring to fit inside of a radius. We will use this primitive to
derive the solution for any number of substrings.
Let the weight of the target parent substring be TW.
Let the weight of the target left substring be TL.
Let the weight of the target right substring be TR.
Let the weight of the search parent substring be SW.
Let the weight of the search left substring be SL.
Let the weight of the search right substring be SR.
TR = TW - TL
SR = SW - SL
Let the sum of substring weight differences be SOD.
SOD = abs(TL - SL) + abs(TR - SR)
We are searching for TL that satisfy SOD <= radius. The SOD has two
inflection points that come from the two abs in its expression. Between
those two inflection points there are only four possible combinations:
TLis going towardsSLandTRis going towardsSR(slope-2).TLhits its its inflection point first and starts going away fromSLandTRis still going towardsSR(slope0).TRhits its its inflection point first and starts going away fromSRandTLis still going towardsSL(slope0).TLandTRhave both hit their inflection points and are going away fromSLandSRrespectively (slope2).
As we can see, regardless of whether TL or TR hit their inflection
point first, we can be guaranteed that the slope is 0 before the final
inflection point. This happens because TL and TR are inversely related.
We must start by computing where the first slope would intersect with the
radius. We assume that TL is below or equal to SL and that TR is
above or equal to SR. Given this, we know that when
(SL - TL) + (TR - SR) = radius we enter the search area. Since
TR = TW - TL we can rewrite this as
(SL - TL) + (TW - TL - SR) = radius. Since SR, SL, and TW are
all known at this point, we can solve for TL:
TL = (-radius + SL - SR + TW) / 2
Lets do the same thing for the opposite case (slope 2 reaches radius):
(TL - SL) + (SR - TR) = radius
(TL - SL) + (SR - TW + TL) = radius
TL = (radius + SL - SR + TW) / 2
We can see that there is a shared intercept between the two equations, but we will not extract the intercept directly because we wouldnt get the same result if we divide by 2 before adding since we would loose a bit of precision.
Let C = SL - SR + TW.
We must search in (-radius + C) / 2..=(radius + C) / 2. However, this
makes the assumption that there are any matches. It is possible that the
radius is low enough that we get no matches. In this case we can test the
0 slope case. We just need to test if TL = (radius + C) / 2 is
actually a match. To test that:
abs((radius + C) / 2 - SL) + abs(TW - (radius + C) / 2 - SR) <= radius.
If the test succeeds, then we can safely iterate over the range.
Lets apply this reasoning to the previously mentioned tree. We expect to
get the range 2..=3.
C = SL - SR + TW = 3 - 2 + 4 = 5
Now we need to test
abs((radius + C) / 2 - SL) + abs(TW - (radius + C) / 2 - SR) <= radius.
abs((1 + 5) / 2 - 3) + abs(4 - (1 + 5) / 2 - 2) <= 1
abs(6 / 2 - 3) + abs(4 - 6 / 2 - 2) <= 1
abs(0) + abs(-1) <= 1
1 <= 1
The test passes. Now we compute the range.
(-radius + C) / 2..=(radius + C) / 2
(-1 + 5) / 2..=(1 + 5) / 2
4 / 2..=6 / 2
2..=3
This is the range we expected.
We may need to clip the range to be inside the bucket as well, since the radius might cover a bigger set of hamming distances than the range.
Now we wish to find all combinations of substrings that result in getting
below the radius. To do this we need to know the SOD at each index we
search in a given substring. To do that we must describe the relationship
between TL and SOD.
There are three phases in the iteration pattern over TL. The first is
when the radius is going down, the second is when it stays flat, the
third is when it is going up. The test in the last part made sure the
bottom was above the radius. We need to compute the points at which the
slope becomes 0, which are the inflection points. Luckily, these are
trivial to calculate. They are when the inside of the abs expressions
in SOD is equal to 0:
TL - SL = 0
TR - SR = 0
We also know that TR = TW - TL, so we can rewrite this in terms of TL:
TW - TL - SR = 0
We care about TL when we hit the inflection point:
TL = SL
TL = -SR + TW
We dont care which inflection point we hit first, we just want to know
where it is. We can just take the min and max of these two
expressions to get the beginning and ending of the flat part of the curve.
Now we want to solve for the SOD. Just like last time, we start with TL
being lower that SL and TR being higher than SR.
(SL - TL) + (TW - TL - SR) = SOD
(TL - SL) + (SR - TW + TL) = SOD
We can simplify these to make it a bit clearer:
C = SL - SR + TW
-2TL + C = SOD
2TL - C = SOD
It starts by going down with a slope of -2 and ends going up with a slope
of 2 just like we expect.
We can use this expression to compute the SOD for each part of iteration.
Now the iteration is split into three parts:
(-radius + C) / 2..SL(SOD = -2TL + C)SL..-SR + TW(SOD = -2SL + C)-SR + TW..=(radius + C) / 2(SOD = 2TL - C)
At this point we can compute the SOD over all of our input indices. Now
we iterate over all input indices specificed, compute their SOD, and then
perform a search over subsequent substrings by passing them a new_radius
of new_radius = radius - SOD. This guarantees that all paths in that
substring also dont exceed the total SOD for all substrings in the level.
Nearest neighbor
When we use the above radius searching algorithm, we search every feature that could be at a particular radius or lower. Unfortunately, when we are searching for nearest neighbors in a hamming weight tree, we must search at radius 0, then radius 1, and so on. If we use the above algorithm, since hamming space has incredibly thick boundaries (see the paper Thick Boundaries in Binary Space and Their Influence on Nearest-Neighbor Search), it can be possible that a great proportion of the entire hamming space is equidistant with the nearest neighbor. This means that our search algorithm will make us test all of those places in the space if they have tables in the tree.
Dependencies
~3.5MB
~59K SLoC