12 releases
| 0.2.12 | Mar 5, 2025 |
|---|---|
| 0.2.11 | Jan 23, 2025 |
| 0.2.8 | Mar 3, 2024 |
| 0.2.7 | Nov 18, 2023 |
| 0.2.2 | Jun 30, 2022 |
#51 in Profiling
432 downloads per month
260KB
3.5K
SLoC
the big-O-test crate
RAM & CPU black-box profiling in tests
The big-O-test crate dynamically analyzes algorithms for space and time resource consumption, allowing tests to enforce a maximum
complexity -- preventing unnoticed performance regressions from making it to your main branch.
Browse the Docs.
It is able to operate both on regular and iterator algorithms -- the later being useful to test CRUD operations.
Reports are issued using the Big O Notation (hence the name) and it works by measuring how the algorithm's CPU times & RAM space requirements grow in relation to the amount of data or number of elements that it is applied on.
By using this crate on tests, you are enforcing -- through real measurements -- how your program should behave in regard to resource consumption -- allowing you to foresee, when in production, the resource requirements and, eventually, helping in the process of optimization, as you are free to do changes that are sure to cause a test failure when regressions in space or time complexities are introduced.
Furthermore, this crate is specially useful to analyse complex algorithms on complex execution scenarios, when a tradicional manual analysis is impossible to be done: a carefully crafted Big O Performance Test is able to investigate/enforce what inputs make up the worse acceptable performance case, best case and how, on average, the algorithm should perform on excerpts of real data.
This crate is, thus, meant to work as a profiling / development tool, alongside with tests & benchmarks.
A distinction is made between regular, non-iterator Algorithms and Iterator Algorithms. The latter encompasses algorithms that operate on a single element per call, which may fit into the following categories:
- those that alter the amount of data they operate on -- such as inserts & deletes
- those that operate on a constant data set -- such as queries, updates and data transformations (eTl)
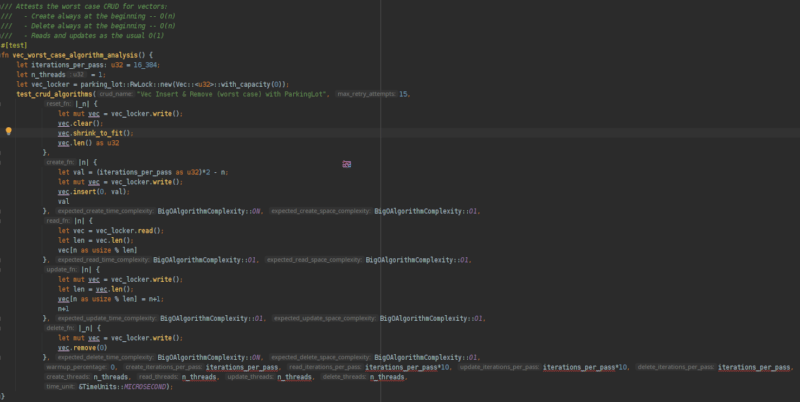
A special method is provided to test CRUD operations, as they should be done following special rules to provide accurate measurements -- see the example bellow:
CRUD test example
Tests CRUD iterator algorithms (called several times per pass, as a single call processes a single element):
The optional measurement/analysis output issued by this test:
Vec Insert & Remove (worst case) with ParkingLot CRUD Algorithm Complexity Analysis:
First Pass (create: 8090µs/+64.42KiB, read: 15254µs/+432.00b, update: 13948µs/+432.00b); Second Pass (create: 22440µs/+64.42KiB, read: 15232µs/+432.00b, update: 13839µs/+432.00b):
'Create' set resizing algorithm measurements:
pass Δt Δs Σn t⁻
1) 8090µs +64.42KiB 16384 0.494µs
2) 22440µs +64.42KiB 32768 1.370µs
--> Algorithm Time Analysis: O(n)
--> Algorithm Space Analysis: O(1) (allocated: 128.20KiB; auxiliary used space: 656.00b)
'Read' constant set algorithm measurements:
pass Δt Δs Σn ⊆r t⁻
1) 15254µs +432.00b 16384 163840 0.093µs
2) 15232µs +432.00b 32768 163840 0.093µs
--> Algorithm Time Analysis: O(1)
--> Algorithm Space Analysis: O(1) (allocated: 208.00b; auxiliary used space: 656.00b)
'Update' constant set algorithm measurements:
pass Δt Δs Σn ⊆r t⁻
1) 13948µs +432.00b 16384 163840 0.085µs
2) 13839µs +432.00b 32768 163840 0.084µs
--> Algorithm Time Analysis: O(1)
--> Algorithm Space Analysis: O(1) (allocated: 208.00b; auxiliary used space: 656.00b)
Delete Passes (2nd: 23365µs/+432.00b; 1st: 7744µs/+432.00b) r=262144:
'Delete' set resizing algorithm measurements:
pass Δt Δs Σn t⁻
1) 7744µs +432.00b 16384 0.473µs
2) 23365µs +432.00b 32768 1.426µs
--> Algorithm Time Analysis: O(n)
--> Algorithm Space Analysis: O(1) (allocated: 208.00b; auxiliary used space: 656.00b)
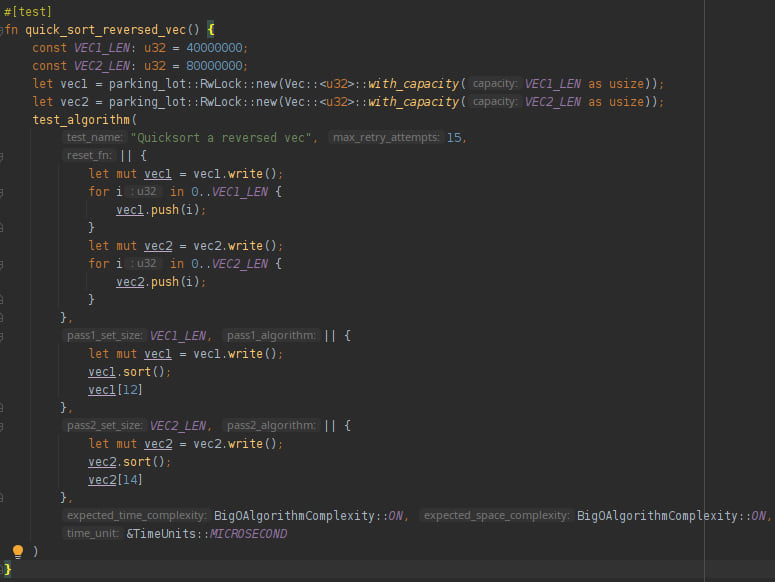
Regular algorithm example
A regular, non-iterator algorithm is run only once for each pass -- in the example bellow, this algorithm is vec::sort():
The optional measurement/analysis output issued by this test:
Running 'Quicksort a reversed vec' algorithm:
Resetting: 3406857µs/+768.00MiB; Pass 1: 658484µs/76.29MiB; Pass 2: 1315255µs/152.59MiB
'Quicksort a reversed vec' regular-algorithm measurements:
pass Δt Δs n s⁻ t⁻
1) 658484µs 76.29MiB 40000000 2b 0.016µs
2) 1315255µs 152.59MiB 80000000 2b 0.016µs
--> Algorithm Time Analysis: O(n)
--> Algorithm Space Analysis: O(n) (allocated: 0.00b; auxiliary used space: 228.88MiB)
Usage in projects
Add this to your Cargo.toml:
[dev-dependencies]
ctor = "0.1"
big-o-test = "0.2"
Then create an Integration Test, setting it up to execute tests linearly (using a single thread) -- see tests/big_o_tests.rs for an example
on how this may be easily achieved.
Note that disabling the Rust's default Parallel Test Runner is crucial for accurately measuring time & memory -- nonetheless, special care was taken to avoid flaky tests: an automatic retrying mechanism kicks in when the time complexity analysis doesn't match the maximum accepted value.
Note
To measure the space resource requirements, this crate sets a custom Global Allocator capable of gathering allocation metrics. It only affects tests, but still imposes a non-negligible overhead -- each allocation / de-allocation updates a dozen atomic counters.
Dependencies
~12–19MB
~72K SLoC