5 unstable releases
Uses old Rust 2015
| 0.3.2 | Mar 3, 2021 |
|---|---|
| 0.3.1 | Mar 30, 2020 |
| 0.3.0 | Jul 10, 2018 |
| 0.2.0 | May 22, 2018 |
| 0.1.0 | Mar 13, 2018 |
#765 in Algorithms
963 downloads per month
Used in pallet-plasm-lockdrop
125KB
697 lines
median
Synopsis
An implementation of an efficient O(n) median filter in Rust.
Motivation
The median filter is a nonlinear digital filtering technique, often used to remove noise from an image or signal. Such noise reduction is a typical pre-processing step to improve the results of later processing […]. Median filtering is very widely used […] because, under certain conditions, it preserves edges while removing noise, also having applications in signal processing. (Wikipedia)
Median vs. Mean
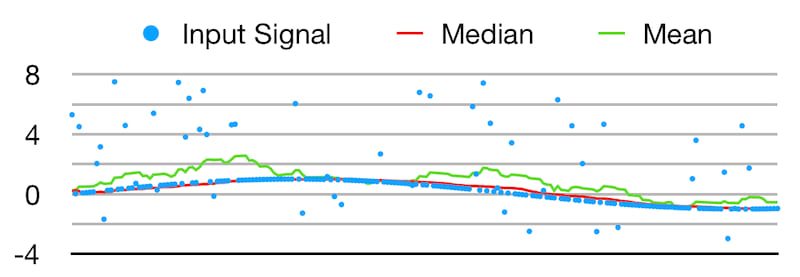
Usage
extern crate rand;
use rand::{Rng, XorShiftRng};
extern crate median;
use median::Filter;
let mut rng = XorShiftRng::new_unseeded();
let mut filter = Filter::new(FILTER_WIDTH);
for i in 0..INPUT_LENGTH {
let signal = (i as f32).sin();
let noise = rng.gen::<f32>();
let value = signal + (noise * 0.2);
let filtered = filter.consume(value);
// use filtered
}
Implementation
The algorithm makes use of a ring buffer of the same size as its filter window. Inserting values into the ring buffer appends them to a linked list that is embedded inside said ring buffer.
Performance
The classical implementation of a median filter uses an internal buffer that is re-sorted for each input to find the median, leading to inferior performance compared to the use of a linked list embedded in a ring buffer, as used in this crate.
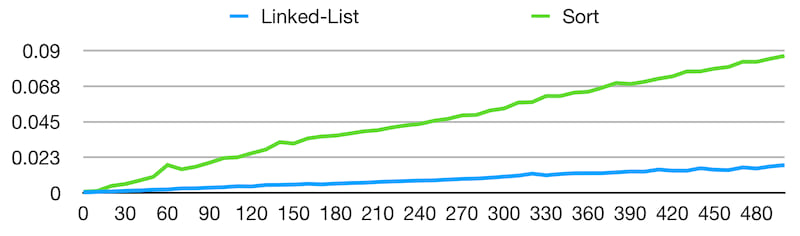 (lower is better)
(lower is better)
Example
Given a sequence of values [3, 2, 4, 6, 5, 1] and a buffer of size 5,
the buffer would be filled like this:
new(5) consume(3) consume(2) consume(4) consume(6) consume(5) consume(1)
▶︎[ ] ▷[3] ┌→[3] ┌→[3]─┐ ┌→[3]─┐ ▶︎┌→[3]─┐ ▷[1]─┐
[ ] ▶︎[ ] ▷└─[2] ▷└─[2] │ ▷└─[2] │ ▷└─[2] │ ▶︎┌─[2]←┘
[ ] [ ] ▶︎[ ] [4]←┘ ┌─[4]←┘ ┌─[4]←┘ └→[4]─┐
[ ] [ ] [ ] ▶︎[ ] └→[6] │ [6]←┐ ┌→[6] │
[ ] [ ] [ ] [ ] ▶︎[ ] └→[5]─┘ └─[5]←┘
Algorithm
- Remove node at current cursor (
▶︎) from linked list, if it exists. (by re-wiring its predecessor to its successor). - Initialize
currentandmedianindex to first node of linked list (▷). - Walk through linked list, searching for insertion point.
- Shift median index on every other hop (thus ending up in the list's median).
- Insert value into ring buffer and linked list respectively.
- Update index to linked list's first node, if necessary.
- Update ring buffer's cursor.
- Return median value.
Contributing
Please read CONTRIBUTING.md for details on our code of conduct,
and the process for submitting pull requests to us.
License
This project is licensed under the MPL-2.0 – see the LICENSE.md file for details.
Dependencies
~510KB
~13K SLoC
