48 releases (breaking)
| 0.33.0 | May 5, 2025 |
|---|---|
| 0.31.0 | Apr 29, 2025 |
| 0.28.0 | Nov 29, 2024 |
| 0.25.0 | Jul 13, 2024 |
| 0.2.0 | Nov 16, 2023 |
#159 in Algorithms
1,017 downloads per month
Used in 2 crates
185KB
4.5K
SLoC
iTriangle
A fast, stable, and robust triangulation library for 2D integer geometry — tested on over 10⁹ randomized inputs.
For detailed performance benchmarks, check out the Performance Comparison
Delaunay
Convex polygons

Steiner points

Tessellation

Centroid net

Features
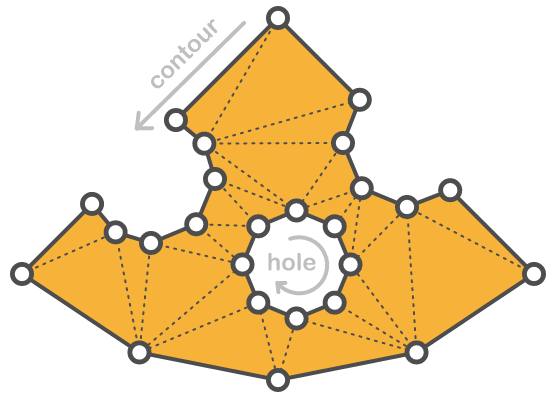
- Raw Triangulation - Fast and simple triangulation of polygons with or without holes.
- Delaunay Triangulation - Efficient and robust implementation for generating Delaunay triangulations.
- Self-Intersection Handling – Fully supports self-intersecting polygons with automatic resolution.
- Adaptive Tessellation - Refine Delaunay triangles using circumcenters for better shape quality.
- Convex Decomposition - Convert triangulation into convex polygons.
- Centroidal Polygon Net: Build per-vertex dual polygons using triangle centers and edge midpoints.
- Steiner Points: Add custom inner points to influence triangulation.
- GPU-Friendly Layout: Triangles and vertices are naturally ordered by X due to the sweep-line algorithm, improving cache locality for rendering.
Reliability
- Extremely Stable: The core triangulation and Delaunay algorithms have been tested against over 1 billion randomized polygon samples.
- Uses pure integer math to avoid floating-point precision issues.
- Designed for use in CAD, EDA, game engines, and any application where robustness is critical.
Demo
Documentation
Getting Started
Add to your Cargo.toml:
[dependencies]
i_triangle = "^0.30.0"
After that, represent your polygon as an array of vertices. Here's an example of a cheese polygon:
use i_triangle::float::triangulatable::Triangulatable;
use i_triangle::float::triangulation::Triangulation;
let shape = vec![
vec![
// body
[0.0, 20.0], // 0
[-10.0, 8.0], // 1
[-7.0, 6.0], // 2
[-6.0, 2.0], // 3
[-8.0, -2.0], // 4
[-13.0, -4.0], // 5
[-16.0, -3.0], // 6
[-18.0, 0.0], // 7
[-25.0, -7.0], // 8
[-14.0, -15.0], // 9
[0.0, -18.0], // 10
[14.0, -15.0], // 11
[26.0, -7.0], // 12
[17.0, 1.0], // 13
[13.0, -1.0], // 14
[9.0, 1.0], // 15
[7.0, 6.0], // 16
[8.0, 10.0], // 17
],
vec![
// hole
[2.0, 0.0], // 0
[5.0, -2.0], // 1
[7.0, -5.0], // 2
[5.0, -9.0], // 3
[2.0, -11.0], // 4
[-2.0, -9.0], // 5
[-4.0, -5.0], // 6
[-2.0, -2.0], // 7
],
];
let triangulation = shape.triangulate().to_triangulation::<u16>();
println!("points: {:?}", triangulation.points);
println!("indices: {:?}", triangulation.indices);
let delaunay_triangulation: Triangulation<[f64; 2], u16> =
shape.triangulate().into_delaunay().to_triangulation();
println!("points: {:?}", delaunay_triangulation.points);
println!("indices: {:?}", delaunay_triangulation.indices);
let convex_polygons = shape.triangulate().into_delaunay().to_convex_polygons();
println!("convex polygons: {:?}", convex_polygons);
let tessellation: Triangulation<[f64; 2], u16> = shape
.triangulate()
.into_delaunay()
.refine_with_circumcenters_by_obtuse_angle(0.0)
.to_triangulation();
println!("points: {:?}", tessellation.points);
println!("indices: {:?}", tessellation.indices);
let centroids = shape
.triangulate()
.into_delaunay()
.refine_with_circumcenters_by_obtuse_angle(0.0)
.to_centroid_net(0.0);
println!("centroids: {:?}", centroids);
Output Triangulation: triangles indices and vertices, where all triangles oriented in a counter-clockwise direction.
Dependencies
~1.3–2.6MB
~63K SLoC