6 releases
| 0.1.5 | Mar 15, 2025 |
|---|---|
| 0.1.4 | Dec 19, 2024 |
| 0.1.3 | Oct 1, 2024 |
| 0.1.1 | Aug 17, 2024 |
#35 in Algorithms
6,751,939 downloads per month
Used in 5,025 crates
(63 directly)
57KB
680 lines
Foldhash
This repository contains foldhash, a fast, non-cryptographic, minimally DoS-resistant hashing algorithm implemented in Rust designed for computational uses such as hash maps, bloom filters, count sketching, etc.
When should you not use foldhash:
-
You are afraid of people studying your long-running program's behavior to reverse engineer its internal random state and using this knowledge to create many colliding inputs for computational complexity attacks. For more details see the section "HashDoS resistance".
-
You expect foldhash to have a consistent output across versions or platforms, such as for persistent file formats or communication protocols.
-
You are relying on foldhash's properties for any kind of security. Foldhash is not appropriate for any cryptographic purpose.
Foldhash has two variants, one optimized for speed which is ideal for data structures such as hash maps and bloom filters, and one optimized for statistical quality which is ideal for algorithms such as HyperLogLog and MinHash.
Foldhash can be used in a #![no_std] environment by disabling its default
"std" feature.
Performance
We evaluated foldhash against three commonly used hashes in Rust:
aHash v0.8.11,
fxhash v0.2.1, and
SipHash-1-3, the default hash algorithm
in Rust at the time of writing. We evaluated both variants foldhash provides,
foldhash-f and foldhash-q, which correspond to foldhash::fast and
foldhash::quality in the crate respectively.
First we note that hashers with random state inflate the size of your HashMap,
which may or may not be important for your performance:
std::mem::size_of::<foldhash::HashMap<u32, u32>>() = 40 // (both variants)
std::mem::size_of::<ahash::HashMap<u32, u32>>() = 64
std::mem::size_of::<fxhash::FxHashMap<u32, u32>>() = 32
std::mem::size_of::<std::collections::HashMap<u32, u32>>() = 48
We tested runtime performance on two machines, one with a 2023 Apple M2 CPU, one
with a 2023 Intel Xeon Platinum 8481C server CPU, both with stable Rust 1.80.1.
Since one of our competitors (aHash) is reliant on AES-based instructions for
optimal performance we have included both a benchmark with and without
-C target-cpu=native for the Intel machine.
We tested across a wide variety of data types we consider representative of types / distributions one might hash in the real world, in the context of a hash table key:
u32- random 32-bit unsigned integers,u32pair- pairs of random 32-bit unsigned integers,u64- random 64-bit unsigned integers,u64pair- pairs of random 64-bit unsigned integers,u64lobits- 64-bit unsigned integers where only the bottom 16 bits vary,u64hibits- 64-bit unsigned integers where only the top 16 bits vary,ipv4-std::net::Ipv4Addr, which is equivalent to[u8; 4],ipv6-std::net::Ipv6Addr, which is equivalent to[u8; 16],rgba- random(u8, u8, u8, u8)tuples,strenglishword- strings containing words sampled uniformly from the top 10,000 most common English words,struuid- random UUIDs, hashed in string representation,strurl- strings containing URLs sampled uniformly from a corpus of 10,000 URLs,strdate- randomYYYY-MM-DDdate strings,accesslog-(u128, u32, chrono::NaiveDate, bool), meant to simulate a typical larger compound type, in this case(resource_id, user_id, date, success)for an access log.kilobyte- random bytestrings one kilobyte in length,tenkilobyte- random bytestrings ten kilobytes in length.
We tested the performance of hashing the above data types in the following four contexts:
hashonly- only the time it takes to hash the value,lookupmiss- the time it takes to do a lookup in a 1,000 element hash map of random elements, only sampling keys of which we know that are not in the hash map,lookuphit- similar tolookupmiss, except the keys are sampled from keys known to be in the hash map,setbuild- the time it takes to construct aHashSetof 1,000 elements from 1,000 randomly sampled elements each repeated 10 times (so 10,000 inserts, with ~90% duplicates).
All times are reported as expected time per operation, so one hash, one lookup,
or one insert respectively. The full results can be found
here. To
summarize, we will only show the results for u64 and strenglishword here, as
well as the observed geometric mean and average rank over the full benchmark.
Xeon 8481c
┌────────────────┬────────────┬────────────┬────────────┬─────────┬─────────┬─────────┐
│ avg_rank ┆ 1.58 ┆ 2.66 ┆ 2.09 ┆ 3.70 ┆ 4.97 │
│ geometric_mean ┆ 6.21 ┆ 7.01 ┆ 7.56 ┆ 8.74 ┆ 28.70 │
╞════════════════╪════════════╪════════════╪════════════╪═════════╪═════════╪═════════╡
│ distr ┆ bench ┆ foldhash-f ┆ foldhash-q ┆ fxhash ┆ ahash ┆ siphash │
╞════════════════╪════════════╪════════════╪════════════╪═════════╪═════════╪═════════╡
│ u64 ┆ hashonly ┆ 0.79 ┆ 1.03 ┆ 0.67 ┆ 1.23 ┆ 9.09 │
│ u64 ┆ lookupmiss ┆ 2.01 ┆ 2.44 ┆ 1.73 ┆ 2.73 ┆ 12.03 │
│ u64 ┆ lookuphit ┆ 3.04 ┆ 3.59 ┆ 2.64 ┆ 3.84 ┆ 12.65 │
│ u64 ┆ setbuild ┆ 6.13 ┆ 6.52 ┆ 4.88 ┆ 6.66 ┆ 17.80 │
| ... ┆ ... ┆ ... ┆ ... ┆ ... ┆ ... ┆ ... |
│ strenglishword ┆ hashonly ┆ 2.63 ┆ 2.98 ┆ 3.24 ┆ 3.57 ┆ 11.87 │
│ strenglishword ┆ lookupmiss ┆ 4.63 ┆ 5.03 ┆ 4.51 ┆ 5.86 ┆ 15.19 │
│ strenglishword ┆ lookuphit ┆ 8.62 ┆ 9.25 ┆ 8.28 ┆ 10.06 ┆ 21.35 │
│ strenglishword ┆ setbuild ┆ 14.77 ┆ 15.57 ┆ 18.86 ┆ 15.72 ┆ 35.36 │
└────────────────┴────────────┴────────────┴────────────┴─────────┴─────────┴─────────┘
Xeon 8481c with RUSTFLAGS="-C target-cpu=native"
┌────────────────┬────────────┬────────────┬────────────┬─────────┬─────────┬─────────┐
│ avg_rank ┆ 1.89 ┆ 3.12 ┆ 2.25 ┆ 2.77 ┆ 4.97 │
│ geometric_mean ┆ 6.00 ┆ 6.82 ┆ 7.39 ┆ 6.94 ┆ 29.49 │
╞════════════════╪════════════╪════════════╪════════════╪═════════╪═════════╪═════════╡
│ distr ┆ bench ┆ foldhash-f ┆ foldhash-q ┆ fxhash ┆ ahash ┆ siphash │
╞════════════════╪════════════╪════════════╪════════════╪═════════╪═════════╪═════════╡
│ u64 ┆ hashonly ┆ 0.79 ┆ 1.01 ┆ 0.67 ┆ 1.34 ┆ 9.24 │
│ u64 ┆ lookupmiss ┆ 1.68 ┆ 2.12 ┆ 1.62 ┆ 1.96 ┆ 12.04 │
│ u64 ┆ lookuphit ┆ 2.68 ┆ 3.19 ┆ 2.28 ┆ 3.16 ┆ 13.09 │
│ u64 ┆ setbuild ┆ 6.16 ┆ 6.42 ┆ 4.75 ┆ 7.03 ┆ 18.88 │
| ... ┆ ... ┆ ... ┆ ... ┆ ... ┆ ... ┆ ... |
│ strenglishword ┆ hashonly ┆ 2.60 ┆ 2.97 ┆ 3.25 ┆ 3.04 ┆ 11.58 │
│ strenglishword ┆ lookupmiss ┆ 4.41 ┆ 4.96 ┆ 4.82 ┆ 4.79 ┆ 32.31 │
│ strenglishword ┆ lookuphit ┆ 8.68 ┆ 9.35 ┆ 8.46 ┆ 8.63 ┆ 21.48 │
│ strenglishword ┆ setbuild ┆ 15.01 ┆ 16.34 ┆ 19.34 ┆ 15.37 ┆ 35.22 │
└────────────────┴────────────┴────────────┴────────────┴─────────┴─────────┴─────────┘
Apple M2
┌────────────────┬────────────┬────────────┬────────────┬─────────┬─────────┬─────────┐
│ avg_rank ┆ 1.62 ┆ 2.81 ┆ 2.02 ┆ 3.58 ┆ 4.97 │
│ geometric_mean ┆ 4.41 ┆ 4.86 ┆ 5.39 ┆ 5.71 ┆ 21.94 │
╞════════════════╪════════════╪════════════╪════════════╪═════════╪═════════╪═════════╡
│ distr ┆ bench ┆ foldhash-f ┆ foldhash-q ┆ fxhash ┆ ahash ┆ siphash │
╞════════════════╪════════════╪════════════╪════════════╪═════════╪═════════╪═════════╡
│ u64 ┆ hashonly ┆ 0.60 ┆ 0.70 ┆ 0.41 ┆ 0.78 ┆ 6.61 │
│ u64 ┆ lookupmiss ┆ 1.50 ┆ 1.61 ┆ 1.23 ┆ 1.65 ┆ 8.28 │
│ u64 ┆ lookuphit ┆ 1.78 ┆ 2.10 ┆ 1.57 ┆ 2.25 ┆ 8.53 │
│ u64 ┆ setbuild ┆ 4.74 ┆ 5.19 ┆ 3.61 ┆ 5.38 ┆ 15.36 │
| ... ┆ ... ┆ ... ┆ ... ┆ ... ┆ ... ┆ ... |
│ strenglishword ┆ hashonly ┆ 1.84 ┆ 2.13 ┆ 1.85 ┆ 2.13 ┆ 11.61 │
│ strenglishword ┆ lookupmiss ┆ 2.71 ┆ 2.96 ┆ 2.47 ┆ 2.99 ┆ 9.27 │
│ strenglishword ┆ lookuphit ┆ 7.54 ┆ 8.77 ┆ 7.83 ┆ 8.77 ┆ 18.65 │
│ strenglishword ┆ setbuild ┆ 16.61 ┆ 17.09 ┆ 14.83 ┆ 16.52 ┆ 26.42 │
└────────────────┴────────────┴────────────┴────────────┴─────────┴─────────┴─────────┘
We note from the above benchmark that for hash table performance the extra
quality that foldhash-q provides is almost never actually worth the small but
also non-negligible computational overhead it has over foldhash-f. This is our
justification for providing foldhash::fast as a default choice for hash
tables, even though it has measurable biases (see also the "Quality" section).
fxhash generally does fairly well for small inputs on the benchmarks, however it
has structural weaknesses as a hash which makes it ill-advised to use as a
general-purpose hash function in our opinion. For example the lookuphit
benchmark on Apple M2 for u64hibits takes 1.77 nanoseconds per lookup for
foldhash, but 67.72 nanoseconds for fxhash (due to everything colliding - the
effects would be even worse with a larger hash map). In our opinion foldhash-f
strikes the right balance between quality and performance for hash tables,
whereas fxhash flies a bit too close to the sun.
aHash is faster than foldhash for medium-long strings when compiled with AES instruction support, but is slower in almost every other scenario or when AES instructions are unavailable.
Quality
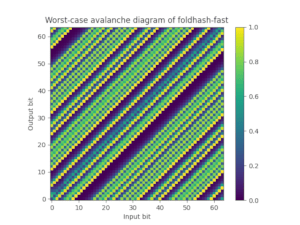
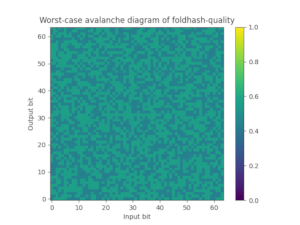
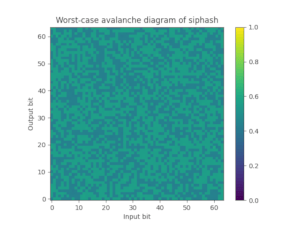
Foldhash-f is a fairly strong hash in terms of collisions on its full 64-bit output. However, statistical tests such as SMHasher3 can distinguish it from an ideal hash function in tests that focus on the relationship between individual input/output bits. One such property is avalanching: changing a single bit in the input does not flip every other bit with 50% probability when using foldhash-f like it should if it behaved like a proper random oracle.
As the benchmarks above show, spending more effort in foldhash-f to improve the hash quality does not lead to better hash table performance. However, there are also use cases for hash functions where it is important that (each bit of) the hash is unbiased and a random function of all bits of the input, such as in algorithms as HyperLogLog or MinHash.
For this purpose we also provide foldhash-q, which is simply a post-processed version of foldhash-f to properly avalanche all the bits. Foldhash-q passes the SMHasher3 test suite without any failures. You can also plot the worst-case probability (where 50% is ideal) that any particular output bit flips if you flip an input bit, which nicely visualizes how fxhash and foldhash-f fail this avalanche property but foldhash-q and SipHash-1-3 pass:
| FxHash | Foldhash-f | Foldhash-q | SipHash-1-3 |
|---|---|---|---|
 |
 |
 |
 |
Background
The name foldhash is derived from the folded multiply. This technique compresses two 64-bit words into a single 64-bit word while simultaneously thoroughly mixing the bits. It does this using a 64 x 64 bit -> 128 bit multiplication followed by folding the two halves of the 128-bit product together using a XOR operation:
let full = (x as u128) * (y as u128);
let lo = full as u64;
let hi = (full >> 64) as u64;
let folded = lo ^ hi;
We're not aware of a formal analysis of this operation, but empirically it works
very well. An informal intuition for why it should work is that multiplication
can be seen as the sum of many shifted copies of one of the arguments, only
including those shifted copies where the other argument has set bits, e.g. for
multiplying 4-bit words abcd and efgh:
abcd * efgh =
abcd * e
abcd * f
abcd * g
abcd * h
--------------- +
Note that the middle bits of the product are a function of many of the input bits, whereas the top-most and bottom-most bits are impacted by fewer of the input bits. By folding the top half back onto the bottom half these effects compensate each other, making all the output bits affected by much of the input.
We did not invent the folded multiply, it was previously used in essentially the same way in aHash, wyhash, and xxhash3. The operation was also used in mum-hash, and probably others. We do not know who originally invented it, the earliest reference we could find was Steven Fuerst blogging about it in 2012.
HashDoS resistance
The folded multiply has a fairly glaring flaw: if one of the halves is zero, the output is zero. This makes it trivial to create a large number of hash collisions (even by accident, as zeroes are a common input to hashes). To combat this, every folded multiply in foldhash has the following form:
folded_multiply(input1 ^ secret1, input2 ^ secret2)
Here secret1 or secret2 are either secret random numbers generated by
foldhash beforehand, or partial hash results influenced by such a secret prior.
This (plus other careful design throughout the hash function) ensures that it is
not possible to create a list of inputs that collide for every instance of
foldhash, and also prevents certain access patterns on hash tables going
quadratric by ensuring that each hash table uses a different seed and thus a
different access pattern. It is these two properties that we refer to when we
claim foldhash is "minimally DoS-resistant": it does the bare minimum to defeat
very simple attacks.
However, to be crystal clear, foldhash does not claim to provide HashDoS resistance against interactive attackers. For a student of cryptography it should be trivial to derive the secret values from direct observation of hash outputs, and feasible to derive the secret values from indirect observation of hashes, such as through timing attacks or hash table iteration. Once an attacker knows the secret values, they can once again create infinite hash collisions with ease.