7 releases
| 0.1.3 | Mar 13, 2022 |
|---|---|
| 0.1.2 | Jan 5, 2022 |
| 0.1.1 | Dec 27, 2021 |
| 0.0.3 | Dec 26, 2021 |
#748 in Math
275KB
804 lines
allan-tools
Allantools (python lib) portage to Rust
This library allows easy computations of Allan deviation & similar statistics.
These statistical methods are mostly used in system stability studies.
Allan and other deviations
Compute Allan deviation over raw data:
use allantools::*;
let taus = tau::generator(tau::TauAxis::Octave, 2, 128); // [2, 4, 8, ... 128]
let sampling_rate = 1.0_f64; // [Hz]
let (dev, errs) = deviation(&data, &taus, Deviation::Allan, sampling_rate, false, false).unwrap();
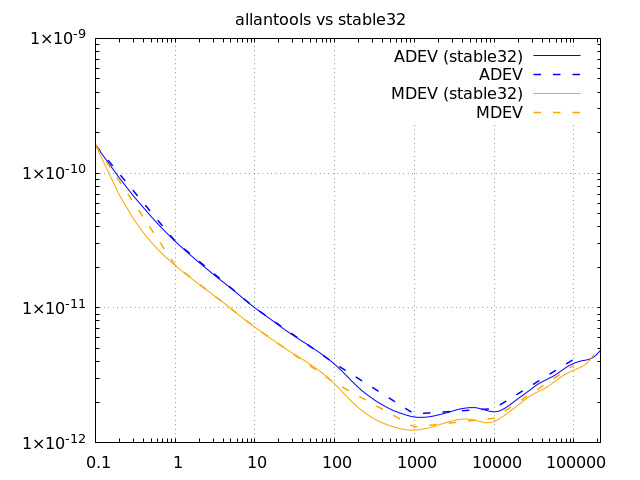
This lib against Time Lab.
Known calculations
- Deviation::Allan
adev - Deviation::Modified
mdev - Deviation::Time
tdev(not fully tested yet) - Deviation::Hadamard
hdev(not fully tested yet) - Deviation::Gcov
gcovallan covariances (not tested yet)
Error bars
Only basic (biased) error bars following the 1/√N decay are currently produced
Overlapping
Improve statiscal confidence by using overlapped formulae
let data: Vec<f64> = some_data();
let taus = tau::generator(tau::TauAxis::Octave, 128);
let overlapping = true;
let sampling_rate = 1.0_f64; // [Hz]
let (var, errs) = deviation(&data, &taus, Deviation::Allan, sampling_rate, false, overlapping).unwrap();
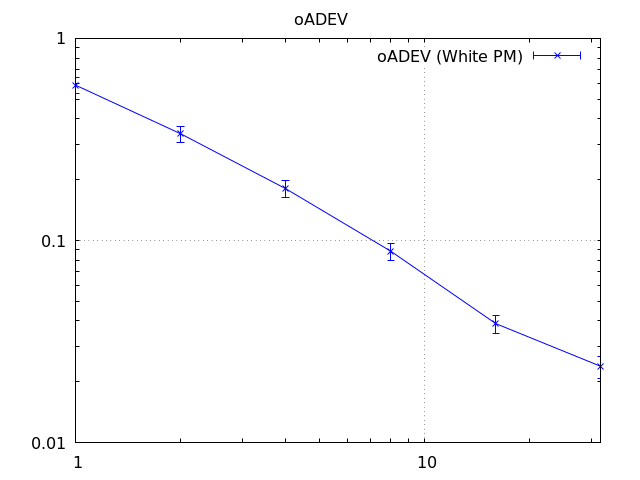
Fractionnal data
is fractional can be used to compute statistics over fractional
(n.a) data:
let data: Vec<f64> = some_data();
let taus = tau::generator(tau::TauAxis::Octave, 10000);
let is_fractional = true;
let sampling_rate = 1.0_f64; // [Hz]
let ( adev, errs) = deviation(&data, &taus, Deviation::Allan, sampling_rate, is_fractional, false).unwrap();
let (oadev, errs) = deviation(&data, &taus, Deviation::Allan, sampling_rate, is_fractional, true).unwrap();
Tau axis generator
The user can pass any τ serie to all computation methods.
This lib integrates a τ axis generator too, which is a convenient method to quickly pass a standard axis to a computation method. Several axis are known:
- TauAxis::Octave is the most efficient
- TauAxis::Decade is the standard and is efficient
- TauAxis::All requires more computation
let taus = tau::generator(tau::TauAxis::Decade, 1.0, 10000.0); // [1.0, 10.0, 100.0, ..., 10000.0]
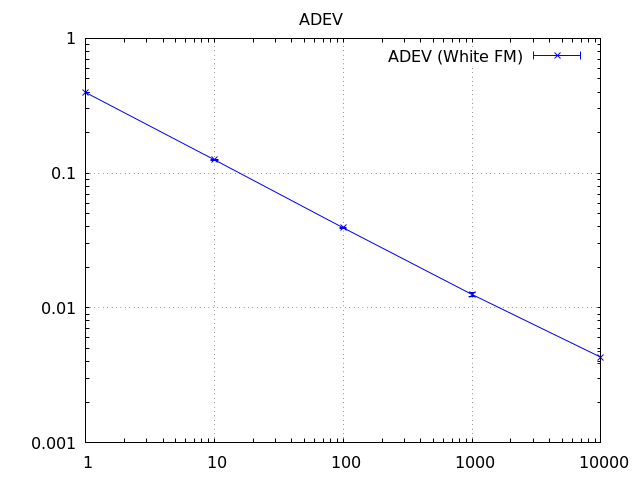
Using TauAxis::All requires more computation but gives a total time granularity
let taus = tau::generator(tau::TauAxis::All, 1.0, 100.0); // [1.0, 2.0, 3.0, ..., 99.0, 100.0]
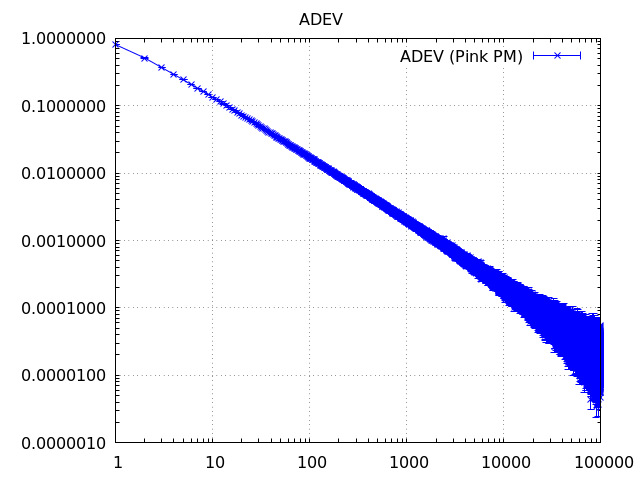
Tau offset and error management
This library computes the requested statistics for all τ values, as long as
$#964;(n) can be evaluated.
If τ (n) cannot be evaluated, computation stops and returns all
previously evaluated offsets.
If not a single τ value is feasible, the lib returns Error::NotEnoughSamplesError
The user must pass a valid τ serie, otherwise:
- TauAxis::NullTauValue: is returned when τ = 0 (non sense) is requested
- TauAxis::NegativeTauValue: is return when τ < 0 (non physical) is requested
- TauAxis::InvalidTauShape: shape is not an increasing (not necessarily steady) shape
Data & Noise generators
Some data generators were integrated or develpped for testing purposes:
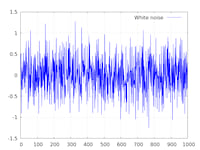
- White noise generator
let x = allantools::noise::white_noise(
-140.0_f64, // dBc/Hz
1.0_f64, // (Hz)
10000); // 10k samples
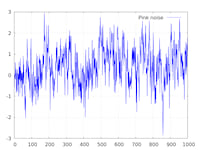
- Pink noise generator
let x = allantools::noise::pink_noise(
-140.0_f64, // dBc @ 1Hz
1.0_f64, // (Hz)
1024); // 1k samples
| Noise | White PM | Flicker PM | White FM | Flicker FM |
|---|---|---|---|---|
| adev | -1 | -1 | -1/2 | 0 |
| mdev | -3/2 | -1 | -1/2 | 0 |
| method | utils::diff(noise::white) | utils::diff(noise::pink) | noise::white | noise::pink |
Power Law Identification
NIST LAG1D autocorrelation
NIST Power Law identification method[[46]]
This macro works well on data serie where one noise process is very dominant.
let r = allantools::nist_lag1d_autocorr(&some_data);
Bias1 + R(n) identification method
TODO
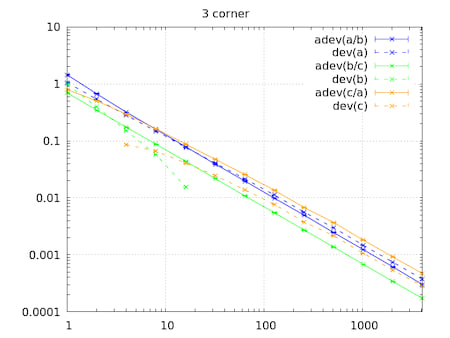
Three Cornered Hat
Three cornered hat fashion statistics, to estimate a/b/c from a against b, b against c and c against a measurements.
let a_against_b = some_measurements("a", "b");
let b_against_c = some_measurements("b", "c");
let c_against_a = some_measurements("c", "a");
let taus = tau::tau_generator(tau::TauAxis::Octave, 10000.0);
let sampling_rate = 1.0;
let is_fractionnal = false;
let overlapping = true;
let ((dev_a, err_a),(dev_b,err_b),(dev_c,err_c)) =
three_cornered_hat(&a_against_b, &b_against_c, &c_against_a,
&taus, sampling_rate, is_fractionnal, overlapping, Deviation::Allan).unwrap();
Tools & utilities
cumsum : (python::numpy like) returns cummulative sum of a serie
let data: Vec<f64> = some_data();
allantools::utilities::cumsum(data, None);
allantools::utilities::cumsum(data, Some(10E6_f64)); // opt. normalization
diff : (python::numpy like) returns 1st order derivative of a serie
let data: Vec<f64> = some_data();
allantools::utilities::diff(data, None);
allantools::utilities::diff(data, Some(10E6_f64)); // opt. normalization
random : generates a pseudo random sequence 0 < x <= 1.0
let data = allantools::utilities::random(1024); // 1k symbols
println!("{:#?}", data);
normalize : normalizes a sequence to 1/norm :
let data: Vec<f64> = somedata();
let normalized = allantools::utilities::normalize(
data,
2.0_f64 * std::f64::consts::PI); // 1/(2pi)
to_fractional_frequency : converts a raw data serie to fractional data.
let data: Vec<f64> = somedata(); // sampled @ 10kHz
let fract = allantools::utilities::to_fractional_frequency(data, 10E3); // :)
fractional_integral : converts a serie of fractional measurements to integrated measurements (like fractional frequency (n.a) to phase time (s)).
let data: Vec<f64> = somedata(); // (n.a)
let fract = allantools::utilities::fractional_integral(data, 1.0); // sampled @ 1Hz :)
fractional_freq_to_phase_time : macro wrapper of previous function
phase_to_radians : converts phase time (s) to phase radians (rad)
let data: Vec<f64> = somedata(); // (s)
let data_rad = allantools::utilities::phase_to_radians(data);
Dependencies
~1.7–2.5MB
~48K SLoC