44 releases
| 0.22.3 | Oct 24, 2023 |
|---|---|
| 0.22.2 | Jun 8, 2023 |
| 0.22.1 | May 9, 2022 |
| 0.19.0 | Mar 31, 2022 |
#347 in Algorithms
121 downloads per month
1.5MB
1.5K
SLoC
Subset Sum(dpss)
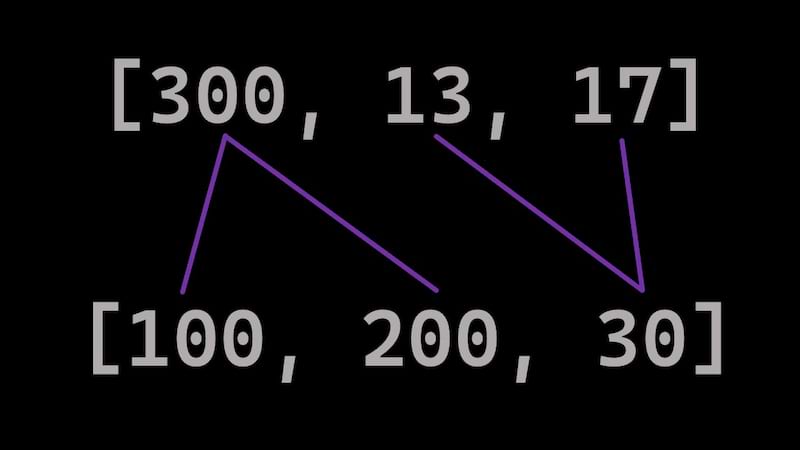
This is a Rust implementation that calculates subset sum problem using dynamic programming. It solves subset sum problem and returns a set of decomposed integers. It also can match corresponding numbers from two vectors and be used for Account reconciliation.
Any feedback is welcome!
There are four ways to use this program.
-
CLI🖥️
-
Rust🦀
-
Web🌎 (This is the easiest way to use.)
-
In python, here is an out of the box example you can run now in google colab. https://colab.research.google.com/github/europeanplaice/subset_sum/blob/main/python/python_subset_sum.ipynb
And it has two methods.
find_subset- It finds a subset from an array.
Sequence Matcher- It finds subset sum relationships with two arrays. Solving multiple subset sub problem.
dpss is short for dynamic programming subset sum.
Links
| Name | URL |
|---|---|
| github | https://github.com/europeanplaice/subset_sum |
| crates.io | https://crates.io/crates/subset_sum |
| docs.rs | https://docs.rs/subset_sum/latest/dpss/ |
| pypi | https://pypi.org/project/dpss/ |
| Website | https://europeanplaice.github.io/subset_sum/ |
CLI
Installation
Binary files are provided on the Releases page. When you download one of these, please add it to your PATH manually.
Usage
Subset sum
First, you need to prepare a text file containing a set of integers like this
1
2
-3
4
5
and save it at any place.
Second, call subset_sum with the path of the text file and the target sum.
Example
Call subset_sum.exe num_set.txt 3 3
The executable's name subset_sum.exe would be different from your choice. Change this example along with your environment.
The second argument is the target sum.
The third argument is the maximum length of the combination.
In this example, the output is
[[2, 1], [4, -3, 2], [5, -3, 1]]
Sequence Matcher
arr1.txt
1980
2980
3500
4000
1050
arr2.txt
1950
2900
30
80
3300
200
3980
1050
20
Call subset_sum.exe arr1.txt arr2.txt 100 100 10 false false
Synopsis:
[executable] [keys text file path] [targets text file path] [max key length] [max target length] [the maximum number of answers] [boolean to use all keys] [boolean to use all targets]
max_key_lengthis used to restrict the number of values in keys chosen.- If
max_key_lengthis 3, an answer's length is at most 3, such as[1980 + 2980 + 3500], [1050] max_target_lengthis the same asmax_key_lengthfor targets.the maximum number of answersspecifies the maximum number of patterns.- If
use_all_keysis true, an answer must contain all the elements of the keys. - If
use_all_targetsis true, an answer must contain all the elements of the targets. - When both
use_all_keysanduse_all_targetsare true, the sum of the keys and the targets must be the same.
In this example, the output is
pattern 1 => [(Sum(1050) -> keys:[1050] == targets:[1050])],
keys remainder : 1980, 2980, 3500, 4000
targets remainder : 20, 30, 80, 200, 1950, 2900, 3300, 3980
pattern 2 => [(Sum(1050) -> keys:[1050] == targets:[1050])
(Sum(12460) -> keys:[1980 + 2980 + 3500 + 4000] == targets:[20 + 30 + 80 + 200 + 1950 + 2900 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 3 => [(Sum(3030) -> keys:[1050 + 1980] == targets:[30 + 1050 + 1950])],
keys remainder : 2980, 3500, 4000
targets remainder : 20, 80, 200, 2900, 3300, 3980
pattern 4 => [(Sum(3030) -> keys:[1050 + 1980] == targets:[30 + 1050 + 1950])
(Sum(10480) -> keys:[2980 + 3500 + 4000] == targets:[20 + 80 + 200 + 2900 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 5 => [(Sum(13510) -> keys:[1050 + 1980 + 2980 + 3500 + 4000] == targets:[20 + 30 + 80 + 200 + 1050 + 1950 + 2900 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 6 => [(Sum(1980) -> keys:[1980] == targets:[30 + 1950])],
keys remainder : 1050, 2980, 3500, 4000
targets remainder : 20, 80, 200, 1050, 2900, 3300, 3980
pattern 7 => [(Sum(2980) -> keys:[2980] == targets:[80 + 2900])],
keys remainder : 1050, 1980, 3500, 4000
targets remainder : 20, 30, 200, 1050, 1950, 3300, 3980
pattern 8 => [(Sum(2980) -> keys:[2980] == targets:[80 + 2900])
(Sum(10530) -> keys:[1050 + 1980 + 3500 + 4000] == targets:[20 + 30 + 200 + 1050 + 1950 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 9 => [(Sum(3500) -> keys:[3500] == targets:[200 + 3300])],
keys remainder : 1050, 1980, 2980, 4000
targets remainder : 20, 30, 80, 1050, 1950, 2900, 3980
pattern 10 => [(Sum(3500) -> keys:[3500] == targets:[200 + 3300])
(Sum(10010) -> keys:[1050 + 1980 + 2980 + 4000] == targets:[20 + 30 + 80 + 1050 + 1950 + 2900 + 3980])],
keys remainder :
targets remainder :
Use in Python
installation
pip install dpss
Usage
find_subset
import inspect
import dpss
help(dpss.find_subset)
>>> find_subset(arr, value, max_length, /)
>>> Finds subsets sum of a target value. It can accept negative values.
>>> # Arguments
>>> * `arr` - An array.
>>> * `value` - The value to the sum of the subset comes.
>>> * `max_length` - The maximum length of combinations of the answer.
print(dpss.find_subset([1, -2, 3, 4, 5], 2, 3))
>>> [[4, -2], [3, -2, 1]]
sequence_matcher
help(dpss.sequence_matcher)
>>> sequence_matcher(keys, targets, max_key_length, max_target_length /)
>>> Finds the integers from two vectors that sum to the same value.
>>> This method assumes that the two vectors have Many-to-Many relationships.
>>> Each integer of the `keys` vector corresponds to the multiple integers of the `targets` vector.
>>> With this method, we can find some combinations of the integers.
>>>
>>> To avoid combinatorial explosion, some parameters need to be set.
>>> `max_key_length` is used to restrict the number of values in keys chosen.
>>> If `max_key_length` is 3, an answer's length is at most 3, such as `[1980 + 2980 + 3500], [1050]`
>>> `max_target_length` is the same as `max_key_length` for targets.
>>> `n_candidates` specifies the maximum number of patterns.
>>> If `use_all_keys` is true, an answer must contain all the elements of the keys.
>>> If `use_all_targets` is true, an answer must contain all the elements of the targets.
>>> When both `use_all_keys` and `use_all_targets` are true, the sum of the keys and the targets must be the same.
>>>
>>> # Arguments
>>> * `keys` - An array.
>>> * `targets` - An array.
>>> * `max_key_length` - An integer.
>>> * `max_target_length` - An integer.
>>> * `n_candidates` - An integer.
>>> * `use_all_keys` - Boolean.
>>> * `use_all_targets` - Boolean.
a = dpss.sequence_matcher(
[1980, 2980, 3500, 4000, 1050],
[1950, 2900, 30, 80, 3300, 200, 3980, 1050, 20], 10, 10, 10, True, True)
print(dpss.sequence_matcher_formatter(a))
pattern 1 => [(Sum(1050) -> keys:[1050] == targets:[1050])
(Sum(12460) -> keys:[1980 + 2980 + 3500 + 4000] == targets:[20 + 30 + 80 + 200 + 1950 + 2900 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 2 => [(Sum(3030) -> keys:[1050 + 1980] == targets:[20 + 30 + 80 + 2900])
(Sum(10480) -> keys:[2980 + 3500 + 4000] == targets:[200 + 1050 + 1950 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 3 => [(Sum(3030) -> keys:[1050 + 1980] == targets:[30 + 1050 + 1950])
(Sum(10480) -> keys:[2980 + 3500 + 4000] == targets:[20 + 80 + 200 + 2900 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 4 => [(Sum(13510) -> keys:[1050 + 1980 + 2980 + 3500 + 4000] == targets:[20 + 30 + 80 + 200 + 1050 + 1950 + 2900 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 5 => [(Sum(4030) -> keys:[1050 + 2980] == targets:[80 + 1050 + 2900])
(Sum(9480) -> keys:[1980 + 3500 + 4000] == targets:[20 + 30 + 200 + 1950 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 6 => [(Sum(1980) -> keys:[1980] == targets:[30 + 1950])
(Sum(11530) -> keys:[1050 + 2980 + 3500 + 4000] == targets:[20 + 80 + 200 + 1050 + 2900 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 7 => [(Sum(2980) -> keys:[2980] == targets:[80 + 2900])
(Sum(10530) -> keys:[1050 + 1980 + 3500 + 4000] == targets:[20 + 30 + 200 + 1050 + 1950 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 8 => [(Sum(3500) -> keys:[3500] == targets:[200 + 3300])
(Sum(10010) -> keys:[1050 + 1980 + 2980 + 4000] == targets:[20 + 30 + 80 + 1050 + 1950 + 2900 + 3980])],
keys remainder :
targets remainder :
pattern 9 => [(Sum(4000) -> keys:[4000] == targets:[20 + 30 + 1050 + 2900])
(Sum(9510) -> keys:[1050 + 1980 + 2980 + 3500] == targets:[80 + 200 + 1950 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 10 => [(Sum(4000) -> keys:[4000] == targets:[20 + 3980])
(Sum(9510) -> keys:[1050 + 1980 + 2980 + 3500] == targets:[30 + 80 + 200 + 1050 + 1950 + 2900 + 3300])],
keys remainder :
targets remainder :
Use in Rust
Please check https://crates.io/crates/subset_sum.
Cargo.toml
[dependencies]
dpss = { version = "(version)", package = "subset_sum" }
Find subset
main.rs
use dpss::dp::find_subset;
fn main() {
let result = find_subset(vec![1, 2, 3, 4, 5], 6, 3);
println!("{:?}", result);
}
Output
[[3, 2, 1], [4, 2], [5, 1]]
Sequence Matcher
main.rs
use dpss::dp::sequence_matcher;
use dpss::dp::sequence_matcher_formatter;
fn main() {
let result = sequence_matcher(&mut vec![1980, 2980, 3500, 4000, 1050], &mut vec![1950, 2900, 30, 80, 3300, 200, 3980, 1050, 20], 10, 10, 10, true, true);
println!("{}", sequence_matcher_formatter(result));
}
Output
pattern 1 => [(Sum(1050) -> keys:[1050] == targets:[1050])
(Sum(12460) -> keys:[1980 + 2980 + 3500 + 4000] == targets:[20 + 30 + 80 + 200 + 1950 + 2900 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 2 => [(Sum(3030) -> keys:[1050 + 1980] == targets:[20 + 30 + 80 + 2900])
(Sum(10480) -> keys:[2980 + 3500 + 4000] == targets:[200 + 1050 + 1950 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 3 => [(Sum(3030) -> keys:[1050 + 1980] == targets:[30 + 1050 + 1950])
(Sum(10480) -> keys:[2980 + 3500 + 4000] == targets:[20 + 80 + 200 + 2900 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 4 => [(Sum(13510) -> keys:[1050 + 1980 + 2980 + 3500 + 4000] == targets:[20 + 30 + 80 + 200 + 1050 + 1950 + 2900 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 5 => [(Sum(4030) -> keys:[1050 + 2980] == targets:[80 + 1050 + 2900])
(Sum(9480) -> keys:[1980 + 3500 + 4000] == targets:[20 + 30 + 200 + 1950 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 6 => [(Sum(1980) -> keys:[1980] == targets:[30 + 1950])
(Sum(11530) -> keys:[1050 + 2980 + 3500 + 4000] == targets:[20 + 80 + 200 + 1050 + 2900 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 7 => [(Sum(2980) -> keys:[2980] == targets:[80 + 2900])
(Sum(10530) -> keys:[1050 + 1980 + 3500 + 4000] == targets:[20 + 30 + 200 + 1050 + 1950 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 8 => [(Sum(3500) -> keys:[3500] == targets:[200 + 3300])
(Sum(10010) -> keys:[1050 + 1980 + 2980 + 4000] == targets:[20 + 30 + 80 + 1050 + 1950 + 2900 + 3980])],
keys remainder :
targets remainder :
pattern 9 => [(Sum(4000) -> keys:[4000] == targets:[20 + 30 + 1050 + 2900])
(Sum(9510) -> keys:[1050 + 1980 + 2980 + 3500] == targets:[80 + 200 + 1950 + 3300 + 3980])],
keys remainder :
targets remainder :
pattern 10 => [(Sum(4000) -> keys:[4000] == targets:[20 + 3980])
(Sum(9510) -> keys:[1050 + 1980 + 2980 + 3500] == targets:[30 + 80 + 200 + 1050 + 1950 + 2900 + 3300])],
keys remainder :
targets remainder :
Dependencies
~2.9–8.5MB
~88K SLoC