1 stable release
| 1.1.4 | Sep 4, 2023 |
|---|---|
| 1.1.3 |
|
| 1.1.1 |
|
#23 in Simulation
36 downloads per month
310KB
7.5K
SLoC
SEUIF97
This is the Rust implementation of the high-speed IAPWS-IF97 package seuif97 with C and Python binding. It is suitable for computation-intensive calculations,such as heat cycle calculations, simulations of non-stationary processes, real-time process monitoring and optimizations.
Through the high-speed package, the results of the IAPWS-IF97 are accurately produced at about 5-20x speed-up compared to using the powi() of the Rust standard library in the forloop directly when computing the basic equations of Region 1,2,3.
The Fast Methods
- The multi-step method unleashes the full power of the compiler optimizations while using
powi()with theforloop - The recursive method computes the polynomial values of the base variable and its derivatives
In the package, 36 thermodynamic, transport and further properties can be calculated.
The following 12 input pairs are implemented:
(p,t) (p,h) (p,s) (p,v)
(t,h) (t,s) (t,v)
(p,x) (t,x) (h,x) (s,x)
(h,s)
Usage
Install the crate
cargo add seuif97
The type of functions are provided in the package:
struct o_id_region_args {
o_id: i32,
region: i32,
}
fn<R>(f64,f64,R) -> f64
where
R: Into<o_id_region_args>,
- the first,second input parameters(f64) : the input propertry pairs
- the third and fourth input parametes:
- the third : the property ID of the calculated property - o_id
- the fourth
optionparameter: the region of IAPWS-IF97
- the return(f64): the calculated property value of o_id
pt<R>(p:f64,t:f64,o_id_region:R)->f64
ph<R>(p:f64,h:f64,o_id_region:R)->f64
ps<R>(p:f64,s:f64,o_id_region:R)->f64
pv<R>(p:f64,v:f64,o_id_region:R)->f64
th<R>(t:f64,h:f64,o_id_region:R)->f64
ts<R>(t:f64,s:f64,o_id_region:R)->f64
tv<R>(t:f64,v:f64,o_id_region:R)->f64
hs<R>(h:f64,s:f64,o_id_region:R)->f64
px(p:f64,x:f64,o_id:i32)->f64
tx(p:f64,x:f64,o_id:i32)->f64
hx(h:f64,x:f64,o_id:i32)->f64
sx(s:f64,x:f64,o_id:i32)->f64
Example
use seuif97::*;
fn main() {
let p:f64 = 3.0;
let t:f64= 300.0-273.15;
let h=pt(p,t,OH);
let s=pt(p,t,OS);
// set the region
let v=pt(p,t,(OV,1));
println!("p={p:.6} t={t:.6} h={t:.6} s={s:.6} v={v:.6}");
}
The C binding
Building the dynamic link library
- cdecl
cargo build -r --features cdecl
- stdcall: Win32 API functions
cargo build -r --features stdcall
The convenient compiled dynamic link libraries are provided in the ./dynamic_lib/
The functions in C
double pt(double p,double t,short o_id);
double ph(double p,double h,short o_id);
double ps(double p,double s,short o_id);
double pv(double p,double v,short o_id);
double tv(double t,double v,short o_id);
double th(double t,double h,short o_id);
double ts(double t,double s,short o_id);
double hs(double h,double s,short o_id);
double px(double p,double x,short o_id);
double tx(double t,double x,short o_id);
double hx(double h,double x,short o_id);
double sx(double s,double x,short o_id);
Example
- ./demo_using_lib/: C, Python, C#, Excel VBA, Java, Fortran
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#define OH 4
#define OS 5
extern double pt(double p,double t,short o_id);
int main(void)
{
double p = 16.0;
double t = 530.0;
double h = pt(p, t, OH);
double s = pt(p, t, OS);
printf("p,t %f,%f h= %f s= %f\n", p, t, h, s);
return EXIT_SUCCESS;
}
The Example of Rankine Cycle Analysis
The Python binding
Install
pip install seuif97
Example
from seuif97 import *
OH=4
p=16.0
t=535.1
# ??(in1,in2,o_id)
h=pt(p,t,OH)
# ??2?(in1,in2)
s=pt2s(p,t)
print(f"p={p}, t={t} h={h:.3f} s={s:.3f}")
Examples
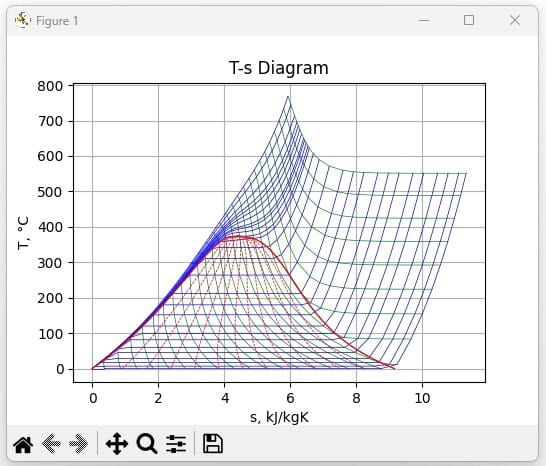
Properties
| Propertry | Unit | Symbol | o_id | o_id(i32) |
|---|---|---|---|---|
| Pressure | MPa | p | OP | 0 |
| Temperature | °C | t | OT | 1 |
| Density | kg/m³ | ρ | OD | 2 |
| Specific Volume | m³/kg | v | OV | 3 |
| Specific enthalpy | kJ/kg | h | OH | 4 |
| Specific entropy | kJ/(kg·K) | s | OS | 5 |
| Specific exergy | kJ/kg | e | OE | 6 |
| Specific internal energy | kJ/kg | u | OU | 7 |
| Specific isobaric heat capacity | kJ/(kg·K) | cp | OCP | 8 |
| Specific isochoric heat capacity | kJ/(kg·K) | cv | OCV | 9 |
| Speed of sound | m/s | w | OW | 10 |
| Isentropic exponent | k | OKS | 11 | |
| Specific Helmholtz free energy | kJ/kg | f | OF | 12 |
| Specific Gibbs free energy | kJ/kg | g | OG | 13 |
| Compressibility factor | z | OZ | 14 | |
| Steam quality | x | OX | 15 | |
| Region | r | OR | 16 | |
| Isobari cubic expansion coefficient | 1/K | ɑv | OEC | 17 |
| Isothermal compressibility | 1/MPa | kT | OKT | 18 |
| Partial derivative (∂V/∂T)p | m³/(kg·K) | (∂V/∂T)p | ODVDT | 19 |
| Partial derivative (∂V/∂p)T | m³/(kg·MPa) | (∂v/∂p)t | ODVDP | 20 |
| Partial derivative (∂P/∂T)v | MPa/K | (∂p/∂t)v | ODPDT | 21 |
| Isothermal throttling coefficient | kJ/(kg·MPa) | δt | OIJTC | 22 |
| Joule-Thomson coefficient | K/MPa | μ | OJTC | 23 |
| Dynamic viscosity | Pa·s | η | ODV | 24 |
| Kinematic viscosity | m²/s | ν | OKV | 25 |
| Thermal conductivity | W/(m.K) | λ | OTC | 26 |
| Thermal diffusivity | m²/s | a | OTD | 27 |
| Prandtl number | Pr | OPR | 28 | |
| Surface tension | N/m | σ | OST | 29 |
| Static Dielectric Constant | ε | OSDC | 30 | |
| Isochoric pressure coefficient | 1/K | β | OPC | 31 |
| Isothermal stress coefficient | kg/m³ | βp | OBETAP | 32 |
| Fugacity coefficient | fi | OFI | 33 | |
| Fugacity | MPa | f* | OFU | 34 |
| Relative pressure coefficient | 1/K | αp | OAFLAP | 35 |
Cite as
- Cheng Maohua. (2023). The Rust implementation of the high-speed IAPWS-IF97 package: SEUIF97 (1.0.9). Zenodo. https://doi.org/10.5281/zenodo.8246380
Dependencies
~0–5MB
~13K SLoC