1 unstable release
| 0.1.0 | Aug 18, 2023 |
|---|
#938 in Images
3.5MB
1K
SLoC
Image Effects
This project is essentially a library for applying effects onto images. It makes heavy use of the image crate since it's the main image processing library for rust, and palette for helping with colour conversions and more - although the project started off with a custom made colour library.
Currently there's two major classes of effect, dithering which works on images and supports both ordered and error propagation methods, and filters such as brightness, contrast, saturation, etc. which work on individual pixels (and therefore also on images).
The following shows which effects are supported on what types.
| dither | filter | |
|---|---|---|
pixel |
no | yes |
image |
yes | yes |
gif |
yes | yes |
pixel=[u8; 3]/[u8; 4]image=Vec<Vec<{pixel}>>/ (image)DynamicImage/ (image)ImageBuffer<Rgb(a)<u8>, Vec<u8>>gif= (image)Frame
(image): from the image crate.
Dithering
Methodology
The 1-bit dithering is separated purely for convenience, since needing to specify a black and white palette every time can be a bit annoying. Internally it just calls the normal error propagation function with a one-bit palette.
Bayer and Basic are separated from the rest in implementation due to how differently they work. Bayer, also known as ordered dithering, doesn't propagate any errors and just manipulates each pixel on the spot using a matrix. Basic, being the naive implementation, simply propagates the error to the right.
All other algorithms are variations on error propagation by using different parameters. As such the implementation works by creating a general error propagation function which takes:
- a
listof propagation offsets - aka where to send the error and by how much. For example if a matrix offers 30 divisions,(1, 0, 5)would point to the next pixel(x+1, y)and send over 5/30ths of the error. - the amount of division. Most algorithms split the error totally - but some like Atkison only propagate some.
After this, each of these algorithms were effectively generated using a macro.
There's two kinds of dithering: Error propagation, and Ordered/Bayer. The only similarity here is that they both will go pixel by pixel, turning them into the closest match in the palette. Measuring which colour is the closest match is done in a different module - colour - more details here.
Error Propagation
For these algorithms, I want to thank Tanner Helland and Efron Licht for their resources. Tanner made a write up on error propagation, including multiple methods that helped to understand the process, and Efron wrote the dither crate which served as an inspiration for this.
So, for error propagation algorithms, after they find the closest match they will then calculate the error - which is essentially the RGB difference between the chosen colour and actual colour. This error is then
propagated to nearby pixels according to what I call the propagation matrix and portion amount.
The propagation matrix is more like a list of coordinates, in addition to how much of the error to propagate - in the form of (dx, dy, portion). For example, (1, 0, 5) will send $\frac{5}{N}$ of the error to the next pixel on the right, where $N$ is the portion amount. Keep in mind that the error does not need to be distributed exactly - for example Atkinson uses 8 portions, but only propagates 6 of them. You can technically also over-propagate, though then you're just adding extra error to the pixels.
Ordered / Bayer
This one works very differently and starts to delve a lot more into the math. For example, here's part of the entire algorithm:
$$ c' = \textrm{nearest_palette_color}(c + r \times (M(x \textrm{ mod } y, y \textrm{ mod } n) - 1/2)) $$
Here, $c'$ is the new colour, $M$ is the threshold map, and $r$ is the amount of spread in color space. I use $r = \frac{255}{3}$ - though in the code it's $\frac{1}{3}$ since rgb values between 0.0 and 1.0 are used. If I'm honest, I don't fully remember where I got this value of $r$ from, but it seems to work quite well.
As for the threshold map, it can be pre-calculated - as the only variable there is the matrix size, which usually comes in powers of two. For more on this, check out the wikipedia page on ordered dithering. They can be pre-calculated, but this library supports any arbitrary size.
Algorithms
Currently supports the following dithering algorithms:
| Name | 1-bit | RGB (Web-safe) | RGB (8-bit) |
|---|---|---|---|
| Floyd-Steinberg |  |
 |
 |
| Jarvis-Judice-Ninke |  |
 |
 |
| Stucki |  |
 |
 |
| Atkinson |  |
 |
 |
| Burkes |  |
 |
 |
| Sierra |  |
 |
 |
| SierraTwoRow |  |
 |
 |
| SierraLite |  |
 |
 |
| Bayer 2x2 |  |
 |
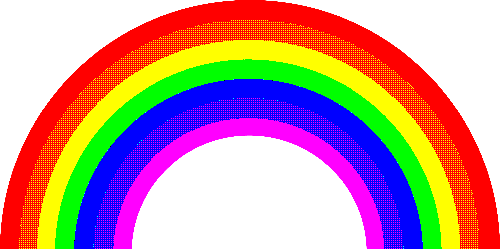 |
| Bayer 4x4 |  |
 |
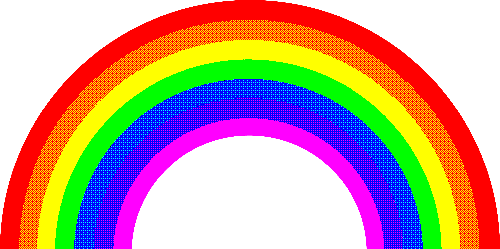 |
| Bayer 8x8 |  |
 |
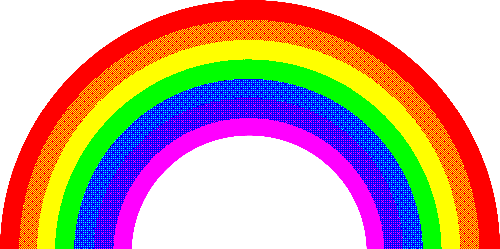 |
| Bayer 16x16 |  |
 |
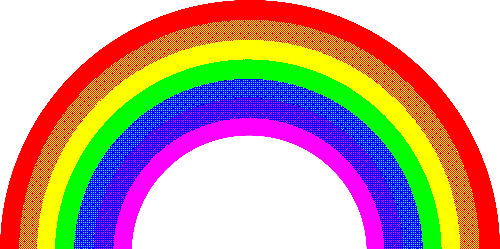 |
Filters
Methodology
For colour, certain filters such as brightness, saturation, hue rotation, are done by first mapping each RGB pixel to HSL or LCH. Originally, HSL was used due to the ease of computation - however LCH is significantly more accurate in representing each of its components.
However, RGB -> LCH requires more computation than RGB -> HSL. Currently the code requires you change it in order to use the right pixel,
but it may be worth looking into allowing the user to use HSL instead for maximal speed.
Algorithms
Currently supports the following effects:
| Name | Image |
|---|---|
| brighten +0.2 |  |
| brighten -0.2 |  |
| saturate +0.2 |  |
| saturate -0.2 |  |
| contrast 0.5 |  |
| contrast 1.5 |  |
| gradient mapping |  |
| rotate hue 180 |  |
| quantize hue |  |
The scale of parameters are as follows:
- brighten: takes
-1.0to1.0. Positive numbers boost the brightness, with 1.0 setting it to maximum luminance - and vice versa. - saturate: same as brighten - a max chroma of 128 is assumed (matching with
palette's documentation) to facilitate the scale. - contrast: takes any float.
x > 1.0increases contrast..x > 0.0 and x < 1.0decreases contrast.- negative contrast obeys a similar scale, where
-1.0is the same as1.0- but with each colour channel being inverted. - might be fun to try doing contrast calculations in other spaces... something for me to look into.
Anything else has a specific type (quantize hue, gradient mapping), or acts as expected (rotate hue)
Colours
At one point, I started implementing all the colour spaces and conversions between them manually. Had a whole sub-library with it - but then I discovered that someone else did it before me way better and ended up throwing away all of my code.
Is what I would say if I wasn't a hoarder.
All of that code is now on colour-exercise-rs - from RGB to HSL to LAB to OKLCH and more - technically not useful as a library since it's better to just use palette, but if you're ever interested in learning about colour - and think seeing someone stumbling through it while they were learning would help - feel free to look!
One remnant of that remains however. colour/comparisons.rs implements multiple distance functions.
colour/comparisons.rs
Methodology
For now, the colour distance function used is weighted euclidean, which looks like this:
$$ f(R, G, B) = \begin{cases} \sqrt{2\Delta R^2 + 4\Delta G^2 + 3\Delta B^2} & \overline{R} < 128, \ \sqrt{3\Delta R^2 + 4\Delta G^2 + 2\Delta B^2} & \textrm{otherwise}, \end{cases} $$
This library also has other distance functions - such as cie76, cie94, and ciede2000. The reason why weighted euclidean is being used instead is mostly for efficiency and because it's been deemed good enough. However the code should be easily changeable to use any of the other functions, so the function used may change / turn into an option.
ciede2000 in particular is significantly more complicated, and may be slower by an order of magnitude. It can likely become more efficient, but as is it's a bit unfeasible for use.
Dependencies
~8.5MB
~135K SLoC