14 releases (breaking)
| 0.11.0 | May 13, 2025 |
|---|---|
| 0.9.0 | Feb 24, 2025 |
| 0.8.0 | Nov 21, 2024 |
| 0.7.1 | Apr 17, 2024 |
| 0.5.1 | Mar 22, 2024 |
#104 in Data structures
94,800 downloads per month
Used in 12 crates
(5 directly)
86KB
1.5K
SLoC
fastbloom
The fastest Bloom filter in Rust. No accuracy compromises. Compatible with any hasher.
Overview
fastbloom is a SIMD accelerated Bloom filter implemented in Rust. fastbloom's default hasher is SipHash-1-3 using randomized keys but can be seeded or configured to use any hasher. fastbloom is 2-400 times faster than existing Bloom filter implementations.
Usage
Due to a different (improved!) algorithm in 0.11.x, BloomFilters have incompatible serialization/deserialization with 0.10.x!
# Cargo.toml
[dependencies]
fastbloom = "0.11.0"
Basic usage:
use fastbloom::BloomFilter;
let mut filter = BloomFilter::with_num_bits(1024).expected_items(2);
filter.insert("42");
filter.insert("🦀");
Instantiate with a target false positive rate:
use fastbloom::BloomFilter;
let filter = BloomFilter::with_false_pos(0.001).items(["42", "🦀"]);
assert!(filter.contains("42"));
assert!(filter.contains("🦀"));
Use any hasher:
use fastbloom::BloomFilter;
use ahash::RandomState;
let filter = BloomFilter::with_num_bits(1024)
.hasher(RandomState::default())
.items(["42", "🦀"]);
Background
Bloom filters are space-efficient approximate membership set data structures supported by an underlying bit array to track item membership. To insert/check membership, a number of bits are set/checked at positions based on the item's hash. False positives from a membership check are possible, but false negatives are not. Once constructed, neither the Bloom filter's underlying memory usage nor number of bits per item change. See more.
hash(4) ──────┬─────┬───────────────┐
↓ ↓ ↓
0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0
↑ ↑ ↑
└───────────┴───────────┴──── hash(3) (not in the set)
Implementation
fastbloom is blazingly fast because it uses L1 cache friendly blocks, efficiently derives many index bits from only one real hash per item, employs SIMD acceleration, and leverages other research findings on Bloom filters.
fastbloom is a partial blocked Bloom filter. Blocked Bloom filters partition their underlying bit array into sub-array "blocks". Bits set and checked from the item's hash are constrained to a single block instead of the entire bit array. This allows for better cache-efficiency and the opportunity to leverage SIMD and SWAR operations when generating bits from an item’s hash. See more on blocked bloom filters. Some of fastbloom's hash indexes span the entire bit array while others are confined to a single block.
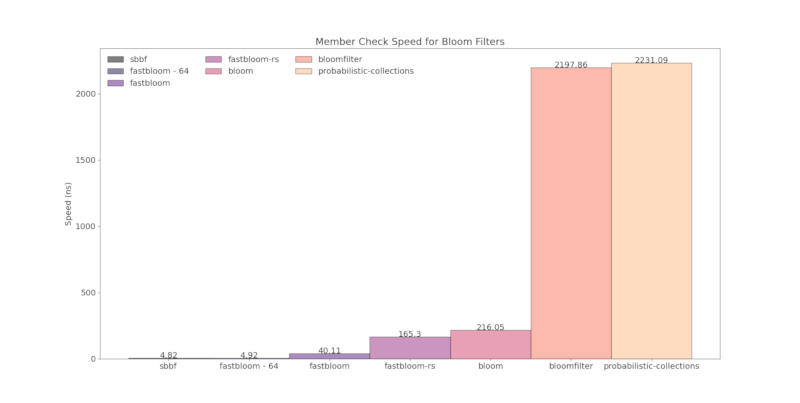
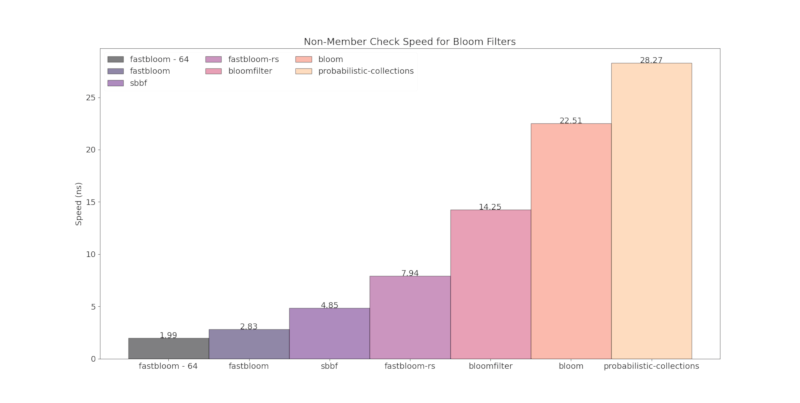
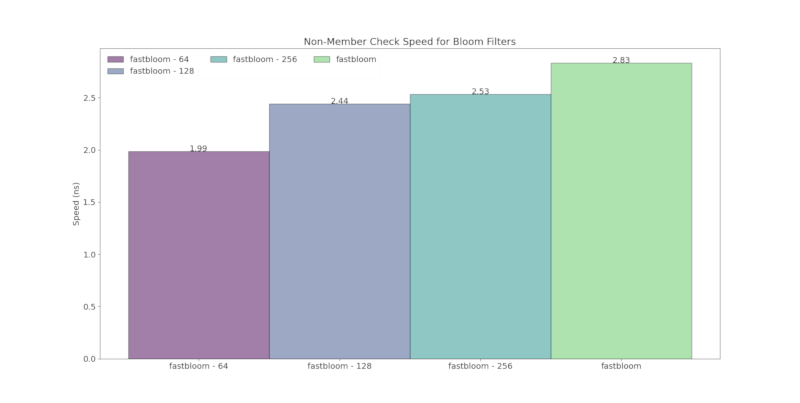
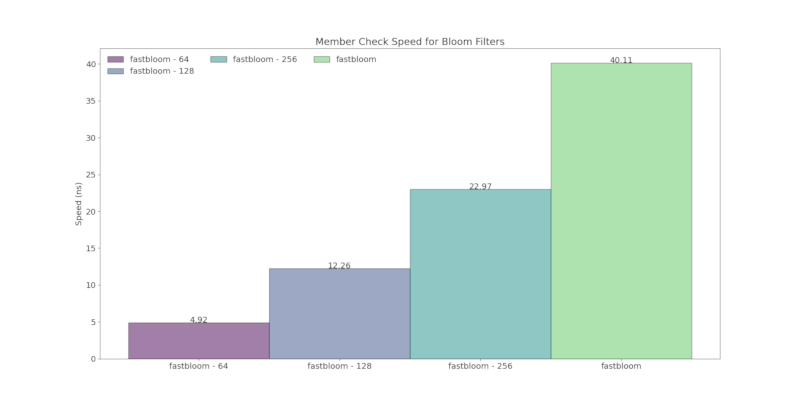
Speed
Below is a comparison of runtime speed with other Bloom filter crates:
- "fastbloom" with default block size of 512 bits and using ahash
- "fastbloom - 64" with block size of 64 bits and using ahash
Hashers used:
- xxhash: sbbf, fastbloom-rs
- Sip1-3: bloom, bloomfilter, probabilistic-collections
- ahash: fastbloom
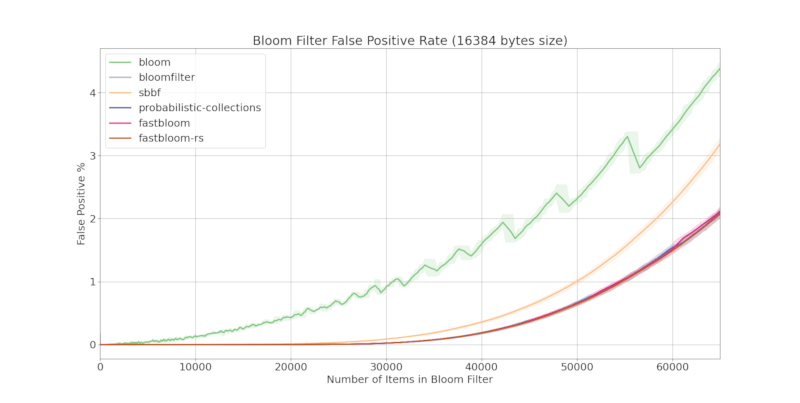
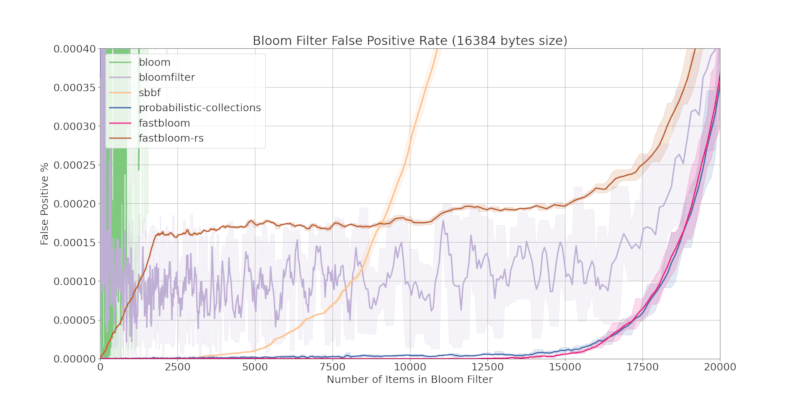
Accuracy
fastbloom does not compromise accuracy. Below is a comparison of false positive rates with other Bloom filter crates:
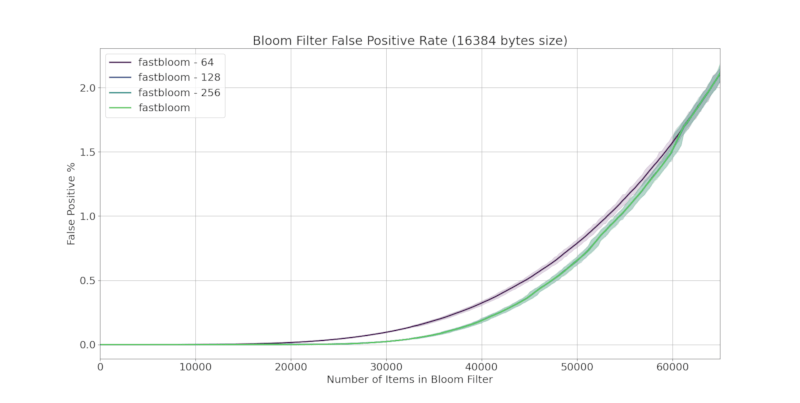
Comparing Block Sizes
fastbloom offers 4 different block sizes: 64, 128, 256, and 512 bits.
use fastbloom::BloomFilter;
let filter = BloomFilter::with_num_bits(1024).block_size_128().expected_items(2);
512 bits is the default. Larger block sizes generally have slower performance but are more accurate, e.g. a Bloom filter with 64 bit blocks is very fast but slightly less accurate.
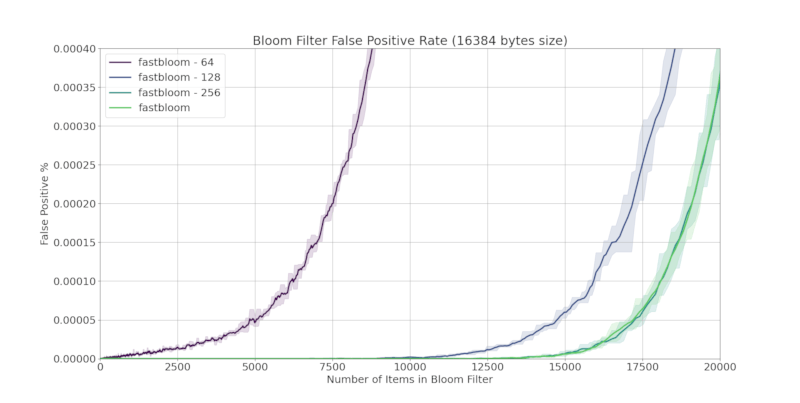
Bloom filters configured using ahash
How it Works
fastbloom attributes its performance to two insights:
- Only one real hash per item is needed, subsequent hashes can be cheaply derived from the real hash using "hash composition"
- Many bit positions can be derived from a few subsequent hashes through SIMD and SWAR-like operations
One Real Hash Per Item
fastbloom employs "hash composition" on two 32-bit halves of an original 64-bit hash. Each subsequent hash is derived by combining the original hash value with a different constant using modular arithmetic and bitwise operations. This results in a set of hash functions that are effectively independent and uniformly distributed, even though they are derived from the same original hash function. Computing the composition of two original hashes is faster than re-computing the hash with a different seed. This technique is explained in depth in this paper.
Many Bit Positions Derived from Subsequent Hashes
Instead of deriving a single bit position per hash, a hash with ~N 1 bits set can be formed by chaining bitwise AND and OR operations of the subsequent hashes.
Example
For a Bloom filter with a bit vector of size 64 and desired hashes 24, 24 (potentially overlapping) positions in the bit vector are set or checked for each item on insertion or membership check respectively.
Other traditional Bloom filters derive 24 positions based on 24 hashes of the item:
hash0(item) % 64hash1(item) % 64- ...
hash23(item) % 64
Instead, fastbloom uses a "sparse hash", a composed hash with less than 32 expected number of bits set. In this case, a ~20 bit set sparse hash is derived from the item and added to the bit vector with a bitwise OR:
hash0(item) & hash1(item) | hash2(item) & hash3(item)
That's 4 hashes versus 24!
Note:
- Given 64 bits, and 24 hashes, a bit has probability (63/64)^24 to NOT be set, i.e. 0, after 24 hashes. The expected number of bits to be set for an item is 64 - (64 * (63/64)^24) ~= 20.
- A 64 bit
hash0(item)provides us with roughly 32 set bits with a binomial distribution.hash0(item) & hash1(item)gives us ~16 set bits,hash0(item) | hash1(item)gives us ~48 set bits, etc.
In reality, the Bloom filter may have more than 64 bits of storage. In that case, many underlying u64s in the block are operated on using SIMD intrinsics. The number of hashes is adjusted to be the number of hashes per u64 in the block. Additionally, some bits may be set in the traditional way, across the entire bit vector, to account for any truncating errors from the sparse hash. This also reduces the false positive rate and boosts non-member check speed.
Available Features
-
rand- Enabled by default, this has theDefaultHashersource its random state usingthread_rng()instead of hardware sources. Getting entropy from a user-space source is considerably faster, but requires additional dependencies to achieve this. Disabling this feature by usingdefault-features = falsemakesDefaultHashersource its entropy usinggetrandom, which will have a much simpler code footprint at the expense of speed. -
serde-BloomFilters implementSerializeandDeserializewhen possible.
References
- Bloom filter - Wikipedia
- Bloom Filter - Brilliant
- Bloom Filter Interactive Demonstration
- Cache-, Hash- and Space-Efficient Bloom Filters
- Less hashing, same performance: Building a better Bloom filter
- A fast alternative to the modulo reduction
License
Licensed under either of
- Apache License, Version 2.0 (LICENSE-APACHE or http://www.apache.org/licenses/LICENSE-2.0)
- MIT license (LICENSE-MIT or http://opensource.org/licenses/MIT)
at your option.
Contribution
Unless you explicitly state otherwise, any contribution intentionally submitted for inclusion in the work by you, as defined in the Apache-2.0 license, shall be dual licensed as above, without any additional terms or conditions.
Dependencies
~2MB
~39K SLoC