9 releases
| 0.3.1 | Feb 19, 2025 |
|---|---|
| 0.3.0 | Feb 19, 2025 |
| 0.2.2 | Feb 19, 2025 |
| 0.1.3 | Feb 19, 2025 |
#421 in Algorithms
764 downloads per month
4.5MB
541 lines
Compressed Integer Vector Library
A Rust library for compressing vectors of u64 integers using instantaneous codes the from dsi-bitstream library. Offers fast random access via sampling to balance speed and memory.
Features
- Efficient Compression: Leverage various codecs like Gamma, Delta, and Rice coding.
- Fast Random Access: Achieve $O(1)$ access with configurable sampling.
- Memory Analysis: Integrate with
mem-dbgfor memory profiling. - Flexible Codecs: Select codecs based on data distribution for optimal compression.
The sampling parameter determines how often full positions are stored to speed up access. Higher values reduce memory overhead but may increase access time. For example, sampling_param = 32 is usually a good trade-off for large datasets.
A Quick Example
Let's consider the universal code Gamma introduced by Elias in the 1960s. This code represents an integer as a unary prefix followed by the binary representation of the integer (thus the name universal, as for every integer x the length of the code is always $O(\log x)$ long, so just a constant factor longer than its binary form). So for example 9 will be encoded as 0001001.
use compressed_intvec::intvec::BEIntVec;
use compressed_intvec::codecs::GammaCodec;
let vec = vec![1, 3, 6, 8, 13, 3];
// The compressed-intvec needs a sampling parameter
let sampling_param = 2; // small since the vector is small
// We are using a convenient type alias for the big-endian representation
let compressed_be = BEIntVec::<GammaCodec>::from(&vec, sampling_param).unwrap();
assert_eq!(compressed_be.get(3), 8);
for (i, val) in compressed_be.iter().enumerate() {
assert_eq!(val, vec[i]);
}
Or alternatively, you can use directly the IntVec specifying the endianness (little-endian in this case):
use compressed_intvec::intvec::IntVec;
use compressed_intvec::codecs::GammaCodec;
use dsi_bitstream::traits::LE;
let vec = vec![1, 3, 6, 8, 13, 3];
let sampling_param = 2; // small since the vector is small
let compressed = IntVec::<LE, _, GammaCodec>::from(&vec, sampling_param).unwrap();
assert_eq!(compressed.get(3), 8);
for (i, val) in compressed.iter().enumerate() {
assert_eq!(val, vec[i]);
}
Available Codecs
| Codec Name | Description |
|---|---|
GammaCodec |
Uses gamma coding without requiring extra runtime parameters. |
DeltaCodec |
Uses delta coding, likewise without extra parameters. |
ExpGolombCodec |
Requires an extra parameter (e.g., a parameter k) for encoding/decoding. |
ZetaCodec |
Uses additional runtime parameters ζ. |
RiceCodec |
Uses a Rice parameter for encoding/decoding. Ideal for skewed distributions. In this case you may want to set this paramater as the floor of the log_2 of the mean of your values |
MinimalBinaryCodec |
A minimal binary code with upper bound u > 0 (truncated binary encoding). This is optimal for uniformly distributed data in the range [0, u). |
ParamZetaCodec |
Parameterized variant of Zeta codec using compile-time flags. |
ParamDeltaCodec |
Parameterized variant of Delta codec using compile-time flags. |
ParamGammaCodec |
Parameterized variant of Gamma codec using compile-time flags. |
For codecs that require extra parameters, we can create a compressed int-vec with the method from_with_param:
use compressed_intvec::intvec::BEIntVec;
use compressed_intvec::codecs::RiceCodec;
let vec = vec![1, 3, 6, 8, 13, 3];
let rice_param = 3; // for example
let sampling_param = 2;
let compressed = BEIntVec::<RiceCodec>::from_with_param(&vec, sampling_param, rice_param).unwrap();
Choosing the right codec is crucial for achieving optimal compression. The efficiency of a codec is highly dependent on the underlying data distribution. For example, Rice coding is usually effective for skewed distributions, while Minimal Binary coding is optimal for uniformly distributed data.
Endianness
The library supports both little-endian and big-endian representations. The IntVec type allows you to specify the endianness at runtime, while the BEIntVec and LEIntVec types provide convenient aliases for big-endian and little-endian representations, respectively.
Memory Analysis (and why choosing the right codec is important)
Both the little-endian and big-endian version of the compressed int-vec include support for the MemDbg/MemSize traits from the mem_dbg crate. For example, this is the output of mem_dbg(DbgFlags::empty() for a very large BEIntVec instance:
11536 B ⏺
10864 B ├╴data
656 B ├╴samples
0 B ├╴codec
8 B ├╴k
8 B ├╴len
0 B ├╴codec_param
0 B ╰╴endian
Consider now a vector of u64 values uniformly distributed in the range [0, u64::MAX) and see it's memory usage
use rand::distr::{Distribution, Uniform};
use rand::SeedableRng;
use mem_dbg::{MemDbg, DbgFlags};
fn generate_uniform_vec(size: usize, max: u64) -> Vec<u64> {
let mut rng = rand::rngs::StdRng::seed_from_u64(42);
let uniform = Uniform::new(0, max).unwrap();
(0..size).map(|_| uniform.sample(&mut rng)).collect()
}
let input_vec = generate_uniform_vec(1000, u64::MAX);
println!("Size of the standard Vec<u64>");
input_vec.mem_dbg(DbgFlags::empty());
This outputs:
Size of the standard Vec<u64>
8024 B ⏺
Next, we compress the vector using both MinimalBinaryCodec and DeltaCodec using for both a sampling parameter of 32:
use compressed_intvec::intvec::BEIntVec;
use compressed_intvec::codecs::{MinimalBinaryCodec, DeltaCodec};
use mem_dbg::{MemDbg, DbgFlags};
use rand::distr::{Distribution, Uniform};
use rand::SeedableRng;
fn generate_uniform_vec(size: usize, max: u64) -> Vec<u64> {
let mut rng = rand::rngs::StdRng::seed_from_u64(42);
let uniform = Uniform::new(0, max).unwrap();
(0..size).map(|_| uniform.sample(&mut rng)).collect()
}
let input_vec = generate_uniform_vec(1000, u64::MAX);
println!("Size of the standard Vec<u64>");
input_vec.mem_dbg(DbgFlags::empty());
let minimal_intvec = BEIntVec::<MinimalBinaryCodec>::from_with_param(&input_vec, 32, 10).unwrap();
let delta_intvec = BEIntVec::<DeltaCodec>::from(&input_vec, 32).unwrap();
println!("Size of the compressed IntVec with MinimalBinaryCodec");
minimal_intvec.mem_dbg(DbgFlags::empty());
println!("\nSize of the compressed IntVec with DeltaCodec");
delta_intvec.mem_dbg(DbgFlags::empty());
The compression results are:
Size of the standard Vec<u64>
8024 B ⏺
Size of the compressed IntVec with MinimalBinaryCodec
832 B ⏺
528 B ├╴data
280 B ├╴samples
0 B ├╴codec
8 B ├╴k
8 B ├╴len
8 B ├╴codec_param
0 B ╰╴endian
Size of the compressed IntVec with DeltaCodec
9584 B ⏺
9288 B ├╴data
280 B ├╴samples
0 B ├╴codec
8 B ├╴k
8 B ├╴len
0 B ├╴codec_param
0 B ╰╴endian
As shown, MinimalBinaryCodec is the most efficient for uniformly distributed data, reducing the size to 832 bytes, an order of magnitude smaller than the original vector. In contrast, DeltaCodec actually increases the size to 9584 bytes, as it is poorly suited for uniform distributions.
Benchmarks
Benchmarks are provided to evaluate both the random access speed and space occupancy of compressed vectors.
- Random Access Benchmarks: These benchmarks measure the time required to access individual elements.
- Space Occupancy Benchmarks: These benchmarks report the memory footprint of various codec configurations and compressed representations.
To run the benchmarks, execute:
cargo bench
The results are output to the terminal and also written to CSV files (e.g. benchmark_space.csv).
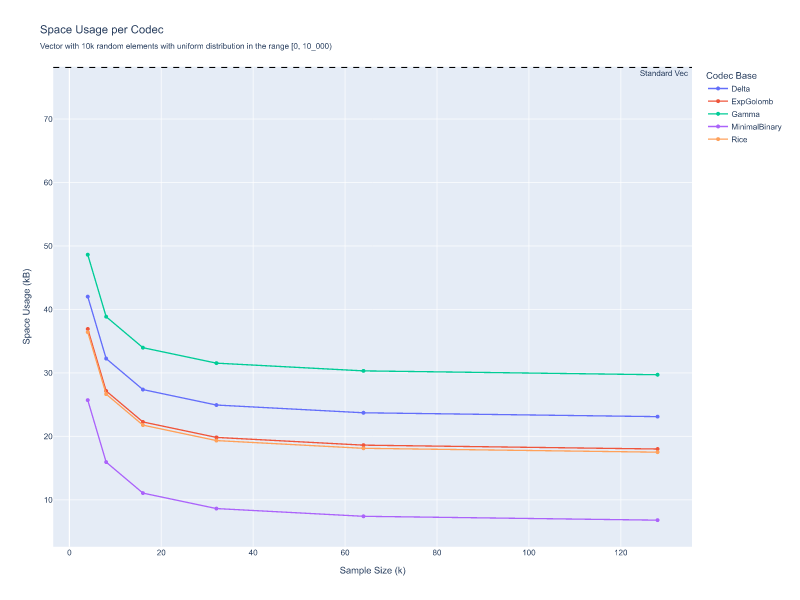
Space Occupancy
In the first graph, the input is a vector of 10k random elements uniformly distributed in the range [0, 10k). Here, all codecs outperform the standard vector in terms of space occupancy, but the MinimalBinaryCodec clearly wins as it is specifically designed for this type of distribution. However, the other codecs also perform well because the range is small.
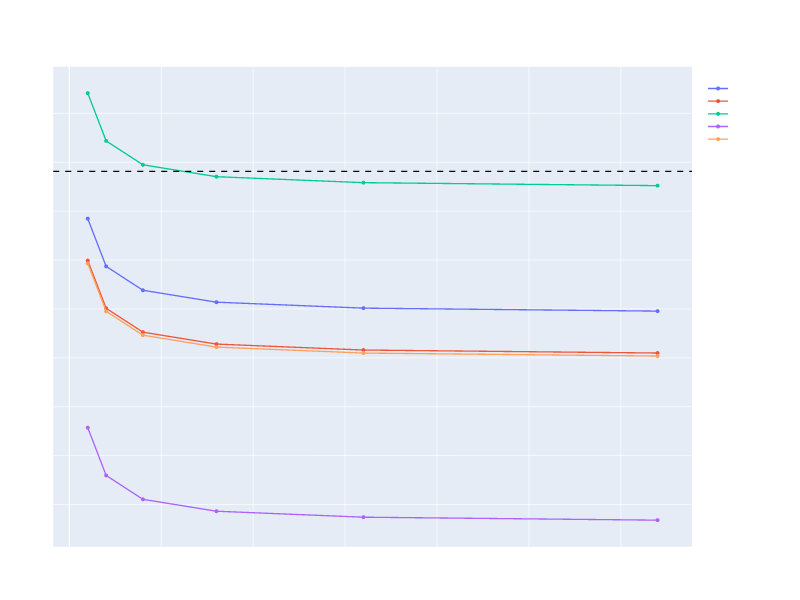
In the second graph, the input is the same vector, but the range is [0, u32::MAX) (viewed as u64). Here, we see that all codecs start to perform poorly, except for MinimalBinaryCodec, which continues to be the best. In particular, codecs like Gamma perform worse than the standard vector.
If we were to increase the range even further, all codecs except MinimalBinaryCodec would perform worse than the standard vector.
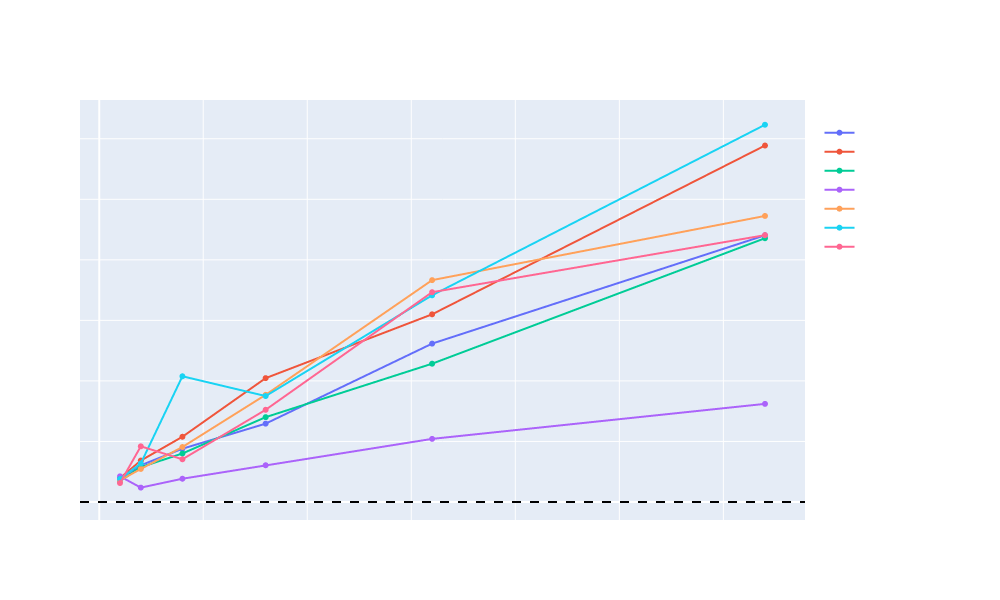
Random Access
Even though in theory the access of this compressed integer vector is $O(1)$, we can't expect it to be as fast as a standard vector. The performance will be affected by the codec used, the distribution of the data and the sampling parameter. However, the benchmarks show that the performance is still quite good, even for large vectors. Choosing as sample rate a value like k = 32 seems to be a good trade-off between memory and speed.
Dependencies
~6–34MB
~416K SLoC