4 releases
| 0.1.8 | Dec 10, 2024 |
|---|---|
| 0.1.7 | Nov 21, 2024 |
#323 in Cryptography
675 downloads per month
Used in reveler
440KB
310 lines
BlueHash Algorithm Documentation - 中文文档
Overview
The BlueHash algorithm is a custom cryptographic hash function designed to generate secure hash values with varying bit lengths (128, 256, and 512 bits). It utilizes multiple rounds of transformations, including state updates, permutation functions, and constant generation, all of which contribute to the uniqueness and security of the final hash output.
This documentation provides an explanation of the algorithm's core components, including the state size, round counts, constant generation, and state update transformations. Mathematical formulas are provided to describe each step in the process.
Use Example
use std::fmt::Write;
use BlueHash::{BlueHashCore, Digest, DigestSize};
fn main() {
// Test Data
let test_data = b"Hello, world! This is a test message for BlueHash!";
// Initialize the BlueHash128 hasher
let mut hasher128 = BlueHashCore::new(DigestSize::Bit128);
hasher128.update(test_data);
let result128 = hasher128.finalize();
println!("BlueHash128 Result: {}", to_hex_string(&result128));
// Initialize the BlueHash256 hasher
let mut hasher256 = BlueHashCore::new(DigestSize::Bit256);
hasher256.update(test_data);
let result256 = hasher256.finalize();
println!("BlueHash256 Result: {}", to_hex_string(&result256));
// Initialize the BlueHash512 hasher
let mut hasher512 = BlueHashCore::new(DigestSize::Bit512);
hasher512.update(test_data);
let result512 = hasher512.finalize();
println!("BlueHash512 Result: {}", to_hex_string(&result512));
}
/// Convert byte array to hex string
fn to_hex_string(bytes: &[u8]) -> String {
let mut hex = String::new();
for byte in bytes {
write!(&mut hex, "{:02x}", byte).unwrap();
}
hex
}
You will get output for example code
BlueHash128 Result: 882864a37a8994e12161d27dfa340df0
BlueHash256 Result: 94cf55cae663dce02e08c3a5660e55ef2e08c3a5660e55ef2e08c3a5660e55ef
BlueHash512 Result: aa9501014ff3013643de6edbcf9d7a4543de6edbcf9d7a4543de6edbcf9d7a4543de6edbcf9d7a4543de6edbcf9d7a4543de6edbcf9d7a4543de6edbcf9d7a45
Key Components
1. State Size and Digest Length
The BlueHash algorithm uses a fixed state size and different digest lengths based on the desired output size.
- State Size: 25 64-bit words, i.e., ( STATE_SIZE = 25 ).
- Digest Length: Based on the digest size, which can be 128, 256, or 512 bits.
The number of rounds and the output length for each digest size are as follows:
$$ R(d) = \begin{cases} 56, & \text{if } d = 128 \text{ bits} \ 64, & \text{if } d = 256 \text{ bits} \ 80, & \text{if } d = 512 \text{ bits} \end{cases} $$
$$ L(d) = \begin{cases} 16, & \text{if } d = 128 \text{ bits} \ 32, & \text{if } d = 256 \text{ bits} \ 64, & \text{if } d = 512 \text{ bits} \end{cases} $$
2. Constants Generation
The generate_constants function generates a unique constant for each round of the hash transformation. The constant is based on several factors, including the round number, input data, and predefined constants.
The constant is generated using the following formula:
$$ \text{constant} = \left( p \ll (r \mod 64) \right) \times \left( r + \text{round factor} \right) \ll 32 + \left( r + \text{round factor} \right) \gg 16 + \text{extra prime} \ll (r \mod 32) + \text{noise} \ll 8 + \text{hash length} $$
Where:
- ( p ) is a fixed prime constant.
- ( r ) is the round number.
round_factoris a function of the round number.extra_primeis a large constant prime.noiseis generated from the input data and round number.hash_lengthis the length of the final digest.
This ensures that each round has a unique constant, enhancing the security and randomness of the hash process.
3. State Update and Permutation
The update and permute functions implement the core transformation logic of the algorithm. Each round involves updating the state using the current round constants and applying various bitwise operations to achieve diffusion and confusion.
The update formula for the state state[i] at round r is as follows:
$$ \text{state}[i] = \left( \text{state}[i] \ll 29 \right) + \text{constant} + \text{local\ vars}[2] \oplus \left( \text{local\ vars}[0] \land \text{local\ vars}[1] \right) \oplus \left( \text{local\ vars}[3] \gg 17 \right) \oplus \left( \text{constant} \ll 23 \right) $$
Where:
state[i]is thei^{th}element of the state array.local varsare variables derived from neighboring state values.<<and>>represent bitwise left and right shifts, respectively.⊕represents the bitwise XOR operation.&represents the bitwise AND operation.
This transformation ensures that each round of the hash function introduces non-linear mixing, which helps in achieving both diffusion (small input changes lead to large output changes) and confusion (output is not easily related to the input).
4. Finalizing the Hash
The final hash is produced by extracting bits from the internal state after all rounds of transformations are complete. The final digest is generated by taking chunks of 64 bits from the state and converting them to bytes.
The formula for generating the final digest is:
$$ \text{digest}[j] = \text{state}\left[\frac{j}{8} \mod \text{STATE\ SIZE}\right] $$
Where:
digest[j]is thej^{th}byte of the final hash.state[j / 8 mod STATE_SIZE]represents the value taken from the state array.
The resulting bytes are concatenated to form the final hash value, which is the output of the finalize function.
5. Correctness and Security
The security of the BlueHash algorithm is based on the following principles:
- Uniqueness: Each round uses a unique constant that depends on the round number, input data, and a series of primes. This ensures that no two rounds produce the same transformation.
- Collision Resistance: The non-linear transformations and mixing of state variables at each round make it computationally difficult to find two distinct inputs that produce the same hash output.
- Diffusion and Confusion: The bitwise operations (XOR, AND, shifts) used in the state update function ensure that small changes in the input lead to significantly different hash values, which is the essence of a good cryptographic hash function.
By adhering to these principles, BlueHash is designed to be a robust cryptographic hash function, resistant to attacks such as collision finding and pre-image attacks.
Compare to SHA-3 (NIST)
| 1500 Sample | SHA3 256 | SHA3 512 | BlueHash 128 | BlueHash 256 | BlueHash 512 |
|---|---|---|---|---|---|
| R^2 | 0.7966978 | 0.7135882 | 0.4950626 | 0.7290226 | 0.6919036 |
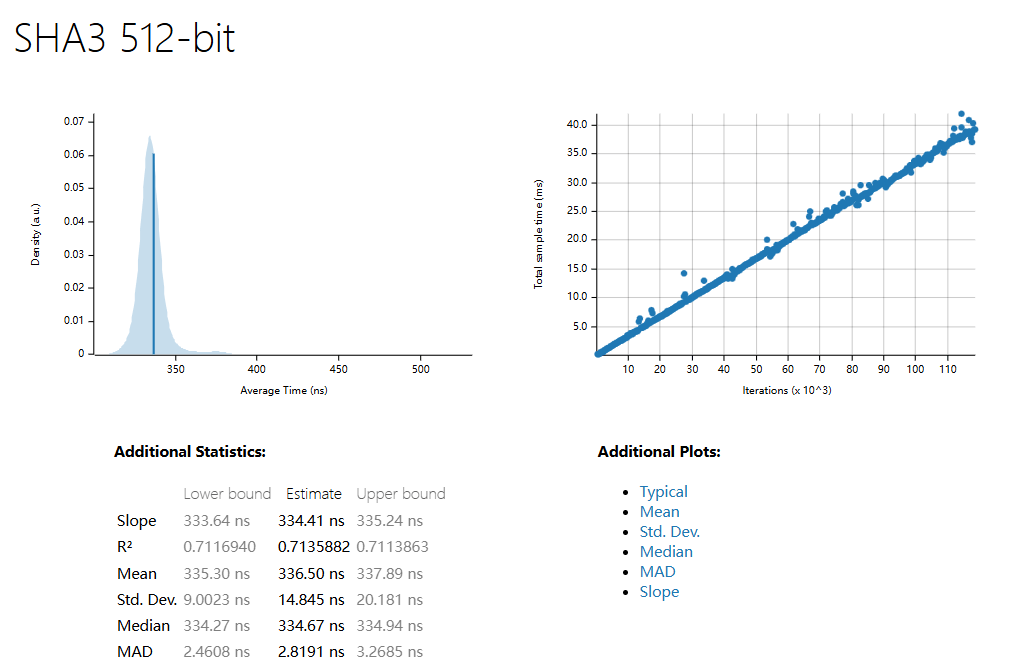
| Mean | 334.45 ns | 336.50 ns | 838.63 µs | 1.0267 ms | 1.3917 ms |
| std. Dev | 19.989 ns | 14.845 ns | 23.557 µs | 20.248 µs | 31.998 µs |
| Median | 333.74 ns | 334.67 ns | 834.35 µs | 1.0234 ms | 1.3859 ms |
| MAD | 3.5463 ns | 2.8191 ns | 10.953 µs | 12.335 µs | 17.597 µs |
BenchMark for BlueHash and SHA3
BlueHash-128 (1500 Samples)

BlueHash-256 (1500 Samples)
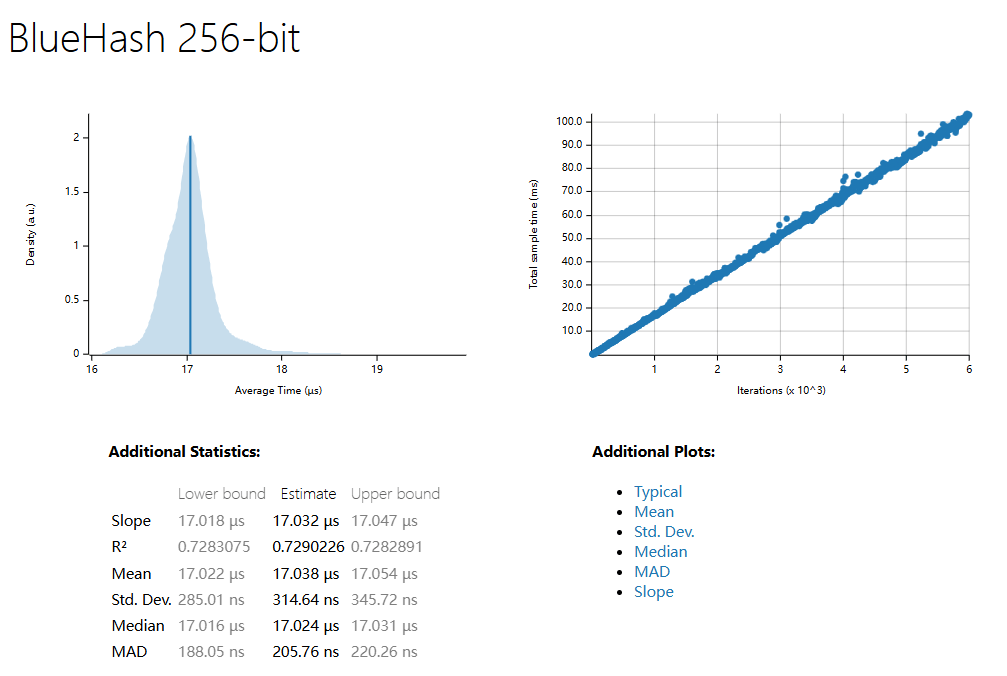
BlueHash-512 (1500 Samples)
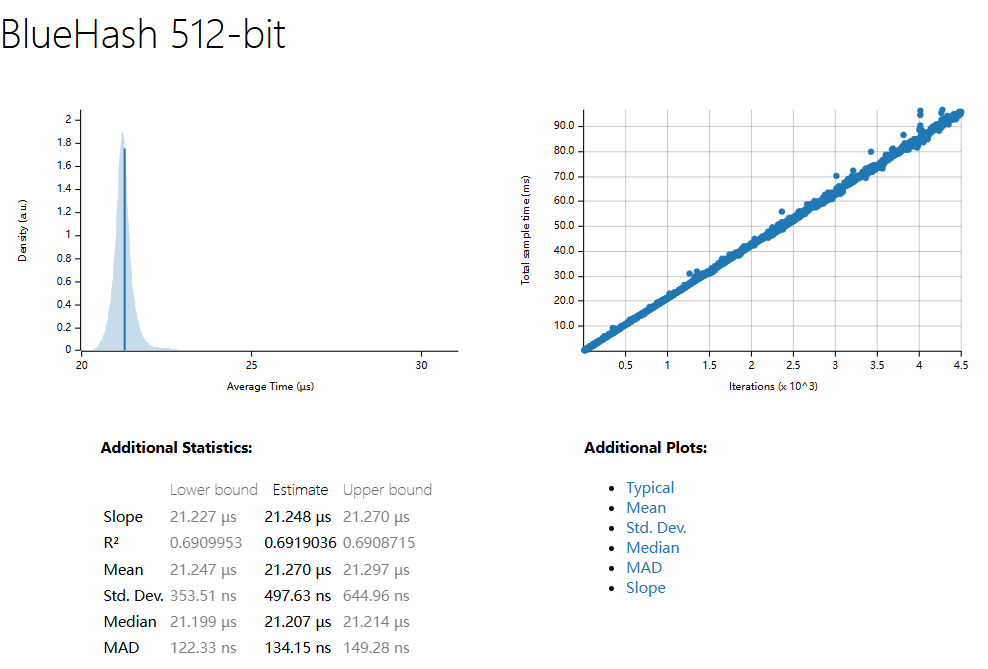
BlueHash Differential Attack (1500 Samples and 10 Million Trial Attack)
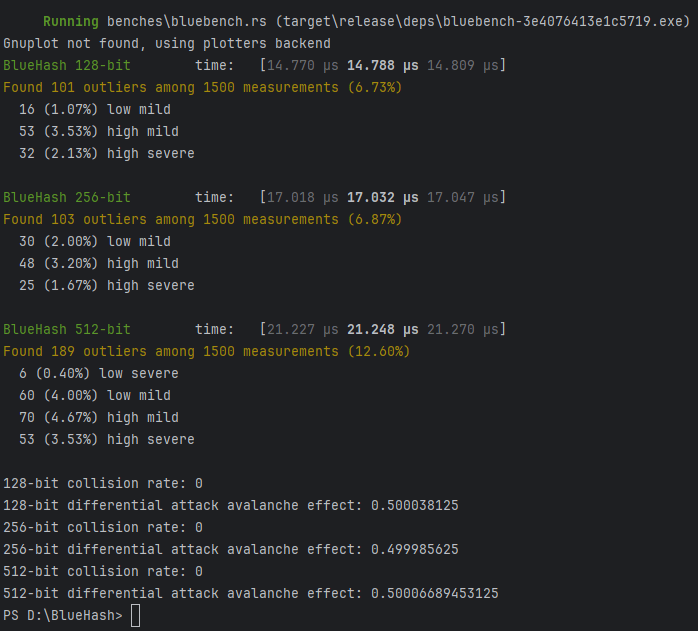
SHA3-256 (1500 Samples)
SHA3-512 (1500 Samples)
What is BlueHash Algorithm Pros and Cons?
The BlueHash algorithm has the following advantages over SHA3-256:
-
Resistance to Quantum Attacks: Provides greater resistance to quantum attacks through the mechanism of LWE noise and constant generation.
-
Higher Randomness and Complexity: Utilizes dynamic generation of constants, increasing the unpredictability of the hash algorithm. This adds complexity and makes the algorithm more resistant to differential attacks.
-
Stronger State Update and Replacement: Offers improved resistance to both conventional and quantum attacks through more diverse bit operations and hybrid operations.
-
Enhanced Noise Generation Mechanism: The addition of LWE noise not only increases security but also enhances defense, particularly against quantum computing.
-
Flexibility: Enables flexible adjustment of rounds and other parameters according to different hash lengths, optimizing performance while ensuring security.
Potential Limitations of BlueHash
-
Higher Performance Overhead: Multiple rounds of complex operations and noise generation increase the computational overhead and may impact efficiency in big data processing.
-
Higher Memory Consumption: More local variables and state storage requirements may lead to performance bottlenecks in low-memory environments.
-
Lack of Standardization and Auditing: Compared to SHA3-256, BlueHash lacks extensive security auditing and community validation, which may affect its trustworthiness in certain applications.
The BlueHash algorithm is a custom cryptographic hash function that leverages multiple rounds of complex transformations to generate secure hashes of varying lengths. It utilizes a fixed state size, round-based transformations, and constant generation to ensure the uniqueness and security of the final output.
Donations
 |
 |
 |
|---|
Dependencies
~8–18MB
~247K SLoC