6 releases
| new 0.1.5 | May 14, 2025 |
|---|---|
| 0.1.4 | Nov 21, 2023 |
#2 in #reconcile
303 downloads per month
175KB
1.5K
SLoC
reconcile-rs
This crate provides a key-data map structure HRTree that can be used together
with the reconciliation Service. Different instances can talk together over
UDP to efficiently reconcile their differences.
All the data is available locally on all instances, and the user can be notified of changes to the collection with an insertion hook.
The protocol allows finding a difference over millions of elements with a limited number of round-trips. It should also work well to populate an instance from scratch from other instances.
The intended use case is a scalable Web service with a non-persistent and eventually consistent key-value store. The design enable high performance by avoiding any latency related to using an external service such as Redis.

In code, this would look like this:
let tree = HRTree::new();
let mut service = Service::new(tree, port, listen_addr, peer_net).await;
tokio::spawn(service.clone().run());
// use the reconciliation service as a key-value store in the API
HRTree
The core of the protocol is made possible by the HRTree (Hash-Range Tree) data structure, which
allows O(log(n)) access, insertion and removal, as well as O(log(n))
cumulated hash range-query. The latter property enables querying
the cumulated (XORed) hash of all key-value pairs between two keys.
Although we did come we the idea independently, it exactly matches a paper published on Arxiv in February 2023: Range-Based Set Reconciliation, by Aljoscha Meyer
Our implementation of this data structure is based on a B-Trees that we wrote
ourselves. Although we put a limited amount of effort in this, did not use
unsafe and have to maintain more invariants, we stay within a factor 2 of the
standard BTreeMap from the standard library:
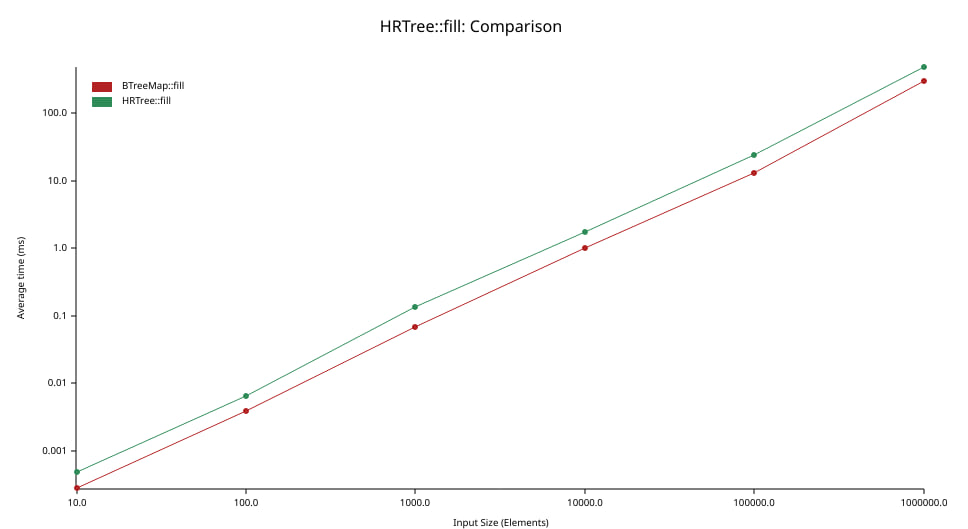
The graph above shows the amount of time in milliseconds (ordinate, left axis) needed to insert N elements (abscissa, bottom axis) in a tree (initially empty). Note that both axes use a logarithmic scale.
The performance of our HRTree implementation follows closely that of
BTreeMap. When looking at each value of N, we see that the average throughput
of the HRTree is between one third and one half that of BTreeMap.

The graph above shows the amount of time in nanoseconds (abscissa, bottom axis) needed to insert a single element (and remove it) in a tree containing N elements (ordinate, bottom axis). Note that both axes use a logarithmic scale.
The most important thing to notice is that the average insertion/removal time only grows from 80 ns to 700 s although the size of the tree changes from 10 to 1,000,000 elements.
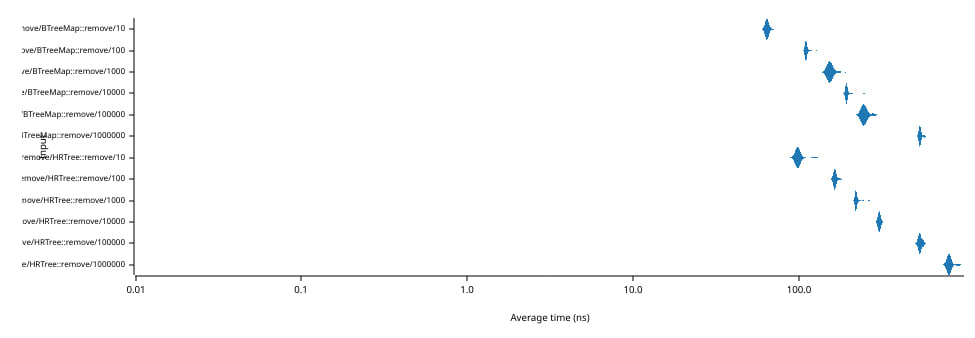
The graph above shows the amount of time in nanoseconds (abscissa, bottom axis) needed to remove a single element (and restore it) from a tree containing N elements (ordinate, bottom axis). Note that both axes use a logarithmic scale.
The most important thing to notice is that the average removal/insertion time only grows from 100 ns to 800 s although the size of the tree changes from 10 to 1,000,000 elements.

The graph above shows the amount of time in microseconds (abscissa, bottom axis) needed to compute 1 cumulated hash over a random range of elements in a tree of size N (ordinate, bottom axis). Note that both axes use a logarithmic scale.
The average time per cumulated hash grows from 30 ns to 1,200 ns as the size of the tree changes from 10 to 1,000,000 elements.
Although there is likely still a lot of room for improvement regarding the
performance of the HRTree, it is quite enough for our purposes, since we
expect network delays to be orders of magnitude longer.
Service
The service exploits the properties of HRTree to conduct a binary-search-like
search in the collections of the two instances. Once difference are found, the
corresponding key-value pairs are exchanged and conflicts are resolved.

The graph above shows the amount of time in microseconds (abscissa, bottom
axis) needed to send 1 insertion, then 1 removal** between two instances of
Service that contain the same N elements (ordinate, left axis). Note that
both axes use a logarithmic scale.
The times are very consistent, hovering around 122 µs, showing that the reconciliation time is entirely bounded by the local network transmission. This is made possible by the immediate transmission of the element at insertion/removal.

The graph above shows the amount of time in milliseconds (abscissa, bottom
axis) needed to reconcile 1 insertion, then 1 removal** between two instances of
Service that contain the same other N elements (ordinate, left axis). Note that
both axes use a logarithmic scale.
This time, the full reconciliation protocol must be run to identify the difference. The times grow from 240 µs to 640 µs as the size of the collection changes from 10 to 1,000,000 elements.
Note: These benchmarks are performed locally on the loop-back network interface. On a real network, transmission delays will make the values larger.
Dependencies
~5–14MB
~158K SLoC