3 releases
| 0.2.2 | Nov 3, 2023 |
|---|---|
| 0.2.1 | Nov 2, 2023 |
| 0.2.0 | Nov 2, 2023 |
#2311 in Algorithms
1,370 downloads per month
38KB
552 lines
rand-unique
A no-std crate for generating sequences of unique random numbers in O(1) time and space. RandomSequence is a non-repeating pseudo-random sequence generator, directly index-able for the nth number in the sequence.
Not cryptographically secure. No-std compatible.
Properties of each RandomSequence:
- Unique: The sequence will only include each number once; every index has a unique output.
- Uniform: The sequence is pseudo-uniformly distributed. Each number which has not yet appeared in the sequence has a roughly equal probability of being the next number in the sequence.
- Fast: Computing the value for any random index in the sequence is an O(1) operation in time and memory complexity.
- Indexable:
RandomSequence::n(index)returns the output for a given position in the sequence. - Integer Range: Support for
u8,u16,u32,u64, andusize. Outputs can be cast toi8,i16,i32,i64, andisizerespectively. - Terminating and Wrapping: Iterator usage of
RandomSequence::next()will terminate at the end of the sequence. Alternatively,RandomSequence::wrapping_next()will wrap around to the start of the sequence when exhausted. - Deterministic: The sequence is deterministic and repeatable for the same seeds.
RandomSequenceBuildercan be serialized with serde to store the sequence parameters. Must have theserdefeature enabled.RandomSequenceBuilder::new(seed_base, seed_offset)can be used to instantiate with specific seeds.RandomSequenceBuilder::rand(prng)can be used to instantiate with random seeds. Must have therandfeature enabled.RandomSequenceBuilder::into_iter()constructs aRandomSequencewith the parameters defined by the builder. Two builders configured the same will generate the same sequence, and so we can construct multiple iterators over the same sequence.
Features
This crate is no-std compatible.
default-features:randrand: Enables therand(&mut RngCore)helper methods onRandomSequenceBuilderandRandomSequenceto initialize with random seeds, which requires theranddependency. Can be omitted and instead manually provide seeds to theRandomSequenceBuilder::seed()method to instantiate.serde: Enables serdeSerlializeandDeserializesupport forRandomSequenceBuilder, which requires theserdedependency.
Example
use std::collections::HashSet;
use rand::rngs::OsRng;
use rand_unique::{RandomSequence, RandomSequenceBuilder};
// Initialise a sequence from a random seed.
let config = RandomSequenceBuilder::<u16>::rand(&mut OsRng);
let mut sequence: RandomSequence<u16> = config.into_iter();
// Iterate over the sequence with next() and prev(), or index directly with n(i).
assert_eq!(sequence.next().unwrap(), sequence.n(0));
assert_eq!(sequence.next().unwrap(), sequence.n(1));
assert_eq!(sequence.next().unwrap(), sequence.n(2));
// Get the current index, if the sequence is not yet exhausted.
assert_eq!(sequence.index(), Some(3));
assert!(!sequence.exhausted());
// Initialise a new RandomSequence iterator over the same sequence.
let sequence_2 = config.into_iter();
assert_eq!(sequence_2.n(0), sequence.n(0));
assert_eq!(sequence_2.index(), Some(0));
// Consume the iterator, and show outputs are unique across the entire type.
// With support for u8, u16, u32, u64, and usize.
let nums: HashSet<u16> = sequence_2.collect();
assert_eq!(nums.len(), u16::MAX as usize + 1);
// Serialise the config to reproduce the same sequence later.
// Requires the "serde" feature to be enabled.
// let config = serde_json::to_string(&sequence.config).unwrap();
Output Distribution
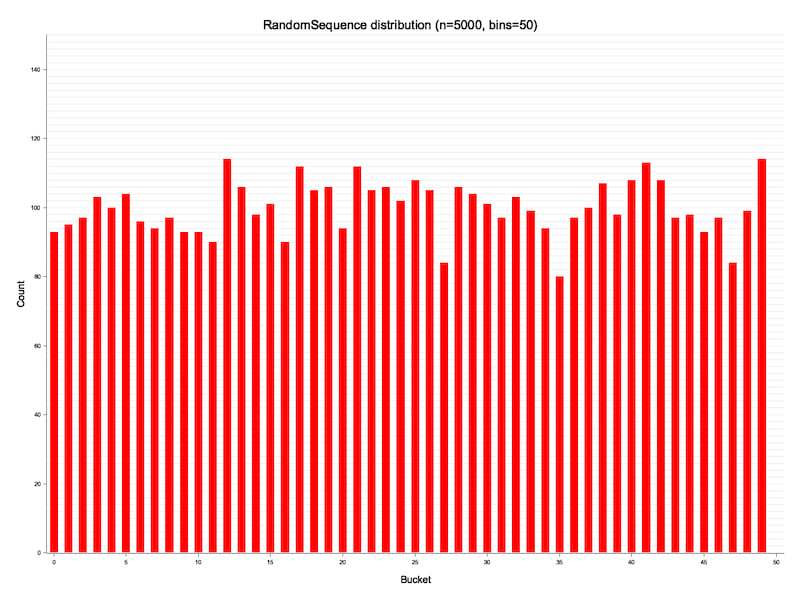
Future work could include a more rigorous analysis of the output distribution. For now, the following charts demonstrate the roughly uniform distribution for RandomSequence<u16>.
Histogram visualisation of the RandomSequence output distribution.
Visual scatter plot of the RandomSequence output.
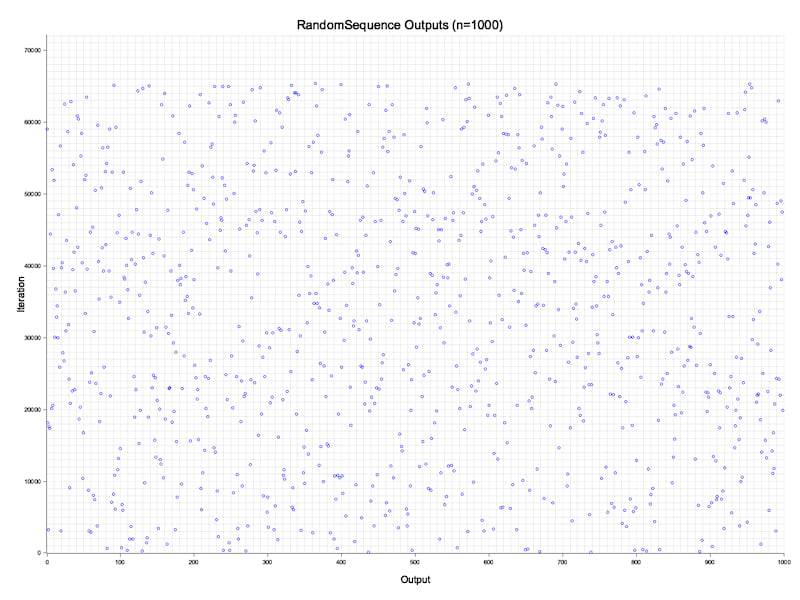
How It Works
This non-repeating pseudo-random number generator works by creating a permutation function against the index in the sequence, herein referred to as x. So for any position x in the sequence, we want to deterministically compute a unique output number via function n(x), where comparing n(x) and n(x + 1) would appear randomly generated.
For any prime number $p$ which satisfies $p 3 \mod 4$, then for any input $x$, the operation $f(x) = x^2 \mod p$ will produce a unique number for each value of $x$ where $2x < p$.
Quadratic residue tends to cluster numbers together, and so we apply the quadratic residue permutation along with other permutation functions (wrapping addition and xor) to add further noise. Permutation functions are those with a direct 1-1 mapping for all inputs to outputs, where each input has a unique output.
In a simplified form, the permutation function is:
/// `p` is chosen to be the largest number satisfying:
/// - a prime number
/// - that satisfies p = 3 mod 4 (`p % 4 == 3`)
/// - that fits in the datatype chosen, in this example `u64`
const PRIME: u64 = 18446744073709551427;
/// Simplified example of the quadratic residue function, taking input `x` for prime `PRIME`.
fn permute_qpr(x: u64) -> u64 {
// we choose x to be the largest prime number of the type, and so there are a small handful
// of numbers in the datatype which are larger than p. We map them directly to themselves.
if x > PRIME {
return x;
}
// compute the residue, in the real method we're careful to avoid integer overflow, omitted here
// for clarity.
let residue = (x * x) % PRIME;
// the residue is unique for all x <= p/2; and so p-residue is also unique for x > p/2.
if x <= PRIME / 2 {
residue
} else {
PRIME - residue
}
}
/// Randomly selected variables to introduce further noise in the output generation.
const OFFSET_NOISE: u64 = 0x46790905682f0161;
const XOR_NOISE: u64 = 0x5bf0363546790905;
/// We can then use this permutation function [permute_qpr] to build our number generator `n(x)`.
fn n(x: u64) -> u64 {
// function sequence: permute_qpr, wrapping addition, xor, permute_qpr
// care is taken in the real implementation to use wrapping addition, omitted here for clarity.
permute_qpr((permute_qpr(x) + OFFSET_NOISE) ^ XOR_NOISE)
}
Sources
Based on the article by @preshing using quadratic prime residue:
Dependencies
~1.5MB
~21K SLoC