2 unstable releases
| 0.1.0 | Apr 27, 2021 |
|---|---|
| 0.0.1 | Oct 10, 2020 |
#628 in Data structures
400KB
5.5K
SLoC
A graph crate with simplicity in mind.
Prepona aims to be simple to use (for users of the crate) and develop further (for contributors). Nearly every function is documented with specifications and examples for users to quickly figure out how to use a specific functionality. Also nearly every implementation has a useful comment about "why" it is implemented this way, So that contributors can quickly read the code and focus on the improvements they want to make.
General Structure
Prepona uses a layered Architecture for the logical relationship between its different components. Each layer expose functionalities for its upper layer to use. From bottom to top:
- Storage: This layer contains different structures that can store information about a graph. Each storage must implement
GraphStoragetrait. This makes swapping out a storage for a different one a trivial task. AlsoGraphStorageprovides default implementation for most of its functions so you can quickly provide an implementation for your custom and incrementally override these default implementation for a custom implementation with higher performance. - Graph: This layer adds more logic and sits on top a storage. One good example is the
SimpleGraphstructure which prevents adding a loop and multiple edges between two vertices. Decoupling this logic from a storage makes it possible to use the storages for any kind of graph. - Provide: This layer contains multiple traits, Each one describing a set of functionalities that is exposed by a graph. For example when a graph implements
Edgestrait, It means graph provides functionalities that enables the user to do computations on the edges of the graph. - Algorithm: This layers contains all the algorithms that can get executed on different kinds of graphs. Note that algorithms do not depend on the graph structure. They depend on the traits defined in the provide layer. This makes it possible to write a generic (in the sense that the algorithm does not depend on any structure but the functionalities that the structure provides) algorithm that can get executed on any type of graph that implements the required traits. For example
TopologicalSortalgorithm requiresVerticesandNeighborstraits to do its computation. So any graph, subgraph, augmented graph, etc... that provides these two traits, is a suitable structure for theTopologicalSortalgorithm to get executed on.
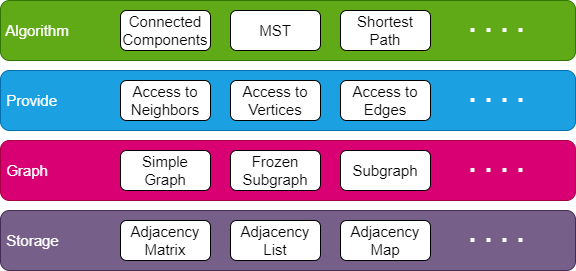
This architecture is meant to ease both the usage and contributing to this project. Users can try out each storage and graph easily without much change needed in the code base. They can easily replace the defaults with their own storage, graph and algorithm. Contributors can pick an area of interest and improve that area without needing to worry about everything else being compatible with their new enhancements.
For more information about each storage, graph, ... check the documentation of the project.
Basic Usage
First you have to pick a storage to use. For this section we will use AdjMatrix.
use prepona::prelude::*;
use prepona::storage::AdjMatrix;
let adj_matrix = AdjMatrix::<usize, DefaultEdge<usize>, UndirectedEdge>::init();
As you can see there are three generic parameters that must be specified. First parameter determines the type of weight is going to be stored in the storage. As you can see we set it to usize because we want our edges to have weights of type usize. Second parameter determines what type of edge is going to be stored. We use DefaultEdge for this example. DefaultEdge has only a weight. But you can define custom edge types. A good example is the FlowEdge which contains weight, capacity and flow. And finally the last parameter determines wether edges are DirectedEdge or UndirectedEdge. We will go with the undirected one for now. This declaration is too long so Prepona provides some aliases to make the process of initializing a storage easier and more readable. For all the aliases exposed by AdjMatrix, visit its documentation page. For now we use the one that is compatible with our defined adj_matrix:
use prepona::storage::Mat;
let adj_matrix = Mat::<usize>::init();
Next we have to find a graph that is suitable for out purpose. For this example we will use SimpleGraph because we don't want loops or multiple edges between two vertices:
use prepona::graph::SimpleGraph;
// Initialize the graph with the storage you have chosen.
let mut graph = SimpleGraph::init(adj_matrix);
Then we can populate our graph with vertices and edges:
// c
//
// a b d e
//
let a = graph.add_vertex();
let b = graph.add_vertex();
let c = graph.add_vertex();
let d = graph.add_vertex();
let e = graph.add_vertex();
// .-- c --.
// | |
// a --- b ----- d --- e
//
let ab = graph.add_edge_unchecked(a, b, 1.into());
let bc = graph.add_edge_unchecked(b, c, 1.into());
let cd = graph.add_edge_unchecked(c, d, 1.into());
let bd = graph.add_edge_unchecked(b, d, 1.into());
let de = graph.add_edge_unchecked(d, e, 1.into());
As you can see we use add_vertex for adding a new vertex to the graph and store the returned id of the vertex in a variable. Then we add the edges (each one with weight equal to 1) using add_edge_unchecked and store the edge ids in their variables. In Prepona each function that has a chance of failure, must provide two versions of itself: A checked version and an unchecked one. In the checked version some lookups will occur before doing the actual computation to make sure the computation is possible. If there is nothing wrong with the state of the graph and passed arguments, checked version of the function will return Ok containing the result of the computation. But if computation could fail, checked version will return an Err with a message explaining what is wrong. But the unchecked version will most likely panic due to some error. Its up to you what version you use. If you are sure about the state of your graph and the arguments you pass to the structure, then use the unchecked version to bypass the lookups and gain more performance. But if you read your values from a source that may produce valid data, use the checked version to prevent panics in your code.
Now we can execute algorithms on our graph. In this example we pretend that this graph represents a network and we want to find those vertices(connection nodes) and edges(links) that if removed, cause our network topology to become disconnected:
use prepona::algo::VertexEdgeCut;
let (cut_vertices, cut_edges) = VertexEdgeCut::init(&graph).execute(&graph);
// We find that vertices b and d are weak points in our topology.
// And if any of them goes down, we will lose connection to part of our network topology.
assert!(
vec![b, d]
.iter()
.all(|vertex_id| cut_vertices.contains(vertex_id))
);
// We find that links a -> b and d -> e are weak links in our topology.
// And if any of them goes down, we will lose connection to part of our network topology.
assert!(
vec![ab, de]
.into_iter()
.all(|edge_id| cut_edges.iter().find(|(_, _, edge)| edge.get_id() == edge_id).is_some())
);
Then you can use this information to alter the topology in order to remove these weak points/links.
Other graph crates
Also checkout these crates:
If you know any other crate email me. I'll be happy to reference them here.
Contribution
This project uses the same code of conduct as rust project.
Try to document your code using the style that already exists in the project code. For example if you are implementing a new algorithm make sure to explain a bit about what the algorithm does, reference a wikipedia page for more info about the algorithm, list the arguments and explain each one, explain the return value and what it means and at last if algorithm can fail, return a Result and avoid panic as much as possible.
Dependencies
~255–345KB
