8 releases
| 0.3.1 | Dec 9, 2024 |
|---|---|
| 0.3.0 | Aug 2, 2024 |
| 0.2.3 | Jul 17, 2024 |
| 0.2.2 | Jun 17, 2024 |
| 0.1.1 | Apr 15, 2024 |
#80 in Concurrency
450 downloads per month
59KB
788 lines
An efficient concurrent ID to object resolver
An IDR (IDentifier Resolver) provides a way to efficiently and concurrently map integer IDs to references to objects. It's particularly useful in scenarios where you need to find objects based on their ID quickly:
- IDs are shared among multiple machines or stored on FS
- IDs are used as a cheaper replacement for
Weaksmart pointers - IDs are used for FFI with untrusted code
The main goal of this crate is to provide a structure for fast getting objects by their IDs. The most popular solution for this problem is concurrent slabs. However, an interesting problem concurrent collections deal with comes from the remove operation. Suppose that a thread removes an element from some lock-free slab while another thread is reading that same element at the same time. The first thread must wait until the second thread stops reading the element. Only then is it safe to destroy it. Thus, every read operation should actually modify memory in order to tell other threads that the item is accessed right now. It can lead to high contention and, hence, a huge performance penalty (see benchmarks below) even if many threads mostly read and don't change data.
The modern solution for this problem is EBR (Epoch-Based memory Reclamation).
This crate is based on the EBR of the sdd crate rather than crossbeam-epoch because it's more efficient.
Every insertion allocates a new EBR container. Thus, it's preferable to use a strong modern allocator (e.g. mimalloc) if insertions are frequent.
Note: this crate isn't optimized for insert/remove operations (although it could be), if it's your case,
check sharded-slab, it's the efficient and well-tested implementation of a concurrent slab.
Examples
Inserting an item into the IDR, and returning a key:
use idr_ebr::{Idr, EbrGuard};
let idr = Idr::default();
let key = idr.insert("foo").unwrap();
let guard = EbrGuard::new();
assert_eq!(idr.get(key, &guard).unwrap(), "foo");
Safety and Correctness
Most implementations of wait-free and lock-free data structures in Rust require some amount of unsafe code, and this crate is not an exception.
Therefore, testing should be as complete as possible, which is why many tools are used to verify correctness:
loomto check concurrency according to C11 memory modelmirito check for the absence of undefined behaviorproptestto check some common properties of the implementation
In order to guard against the ABA problem, this crate makes use of
generational indices. Each slot in the underlying slab tracks a generation
counter, which is incremented every time a value is removed from that slot,
and the keys returned by Idr::insert() include the generation of the slot
when the value was inserted, packed into the high-order bits of the key.
This ensures that if a value is inserted, removed, and a new value is inserted
into the same slot in the underlying slab, the key returned by the first call
to insert will not map to the new value.
Since a fixed number of bits are set aside to use for storing the generation counter, the counter will wrap around after being incremented a number of times. To avoid situations where a returned index lives long enough to see the generation counter wraps around to the same value, it is good to be fairly generous when configuring the allocation of key bits.
Performance
These graphs were produced by benchmarks using the criterion crate.
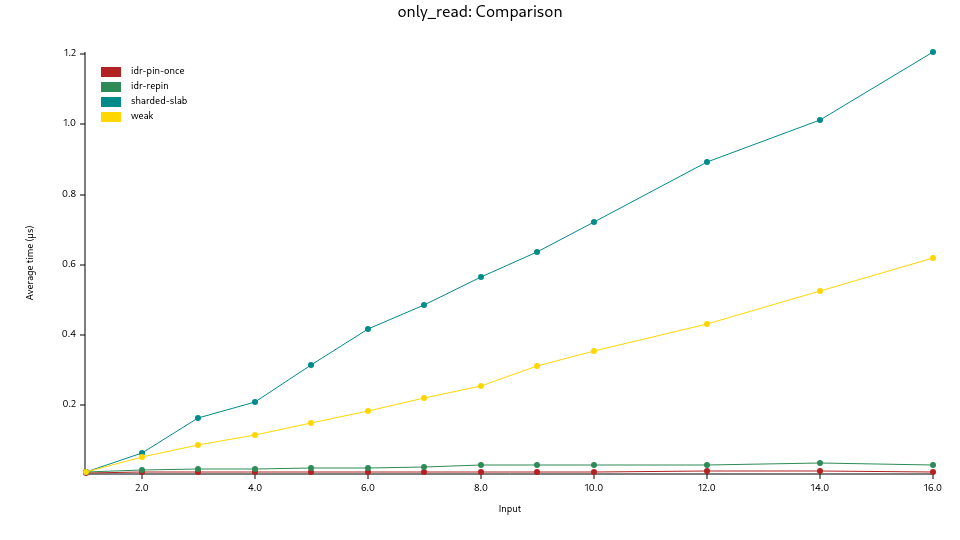
The first shows the results of the read_only benchmark where an increasing
number of threads accessing the same slot, which leads to high contention.
It compares the performance of the IDR with sharded-slab and simple std::sync::Weak::upgrade():
idr-pin-once: oneEbrGuard::new()for all accessesidr-repin: newEbrGuard::new()on every accessweak:std::sync::Weak::upgrade()sharded-slab:Slabwith default parameters in thesharded-slabcrate
This benchmark demonstrates that the IDR doesn't create any contention on get() at all.
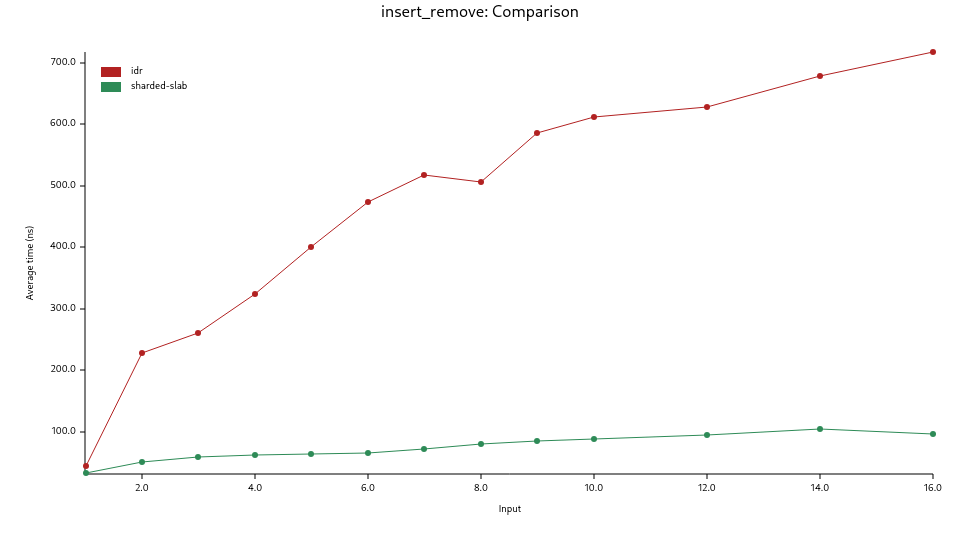
The second graph shows the results of the insert_remove benchmark where an increasing
number of threads insert and remove entries from the IDR. As mentioned before, it's not the goal
of this crate, and not optimized yet for this reason.
idr: theIDRstructure from this cratesharded-slab:Slabfrom thesharded-slabcrate
Implementation
The IDR is based on a slab, where every slot contains a link to the EBR container.
Thus, every Idr::insert() calls an allocator to create that container.
The container can be used by multiple threads both in a temporary way (Idr::get() or Idr::iter())
and permanently (Idr::get_owned()) even when the IDR is already dropped or an entry is removed from the IDR.
The IDR structure:
IDR pages slots
#─►┌───────────┐ ┌───►┌──────────┐
│ page #0 │ │ ┌►│ next │
├───────────┤ │ │ ├──────────┤
│ page #1 │ │ │ │generation│
│ slots ─┼──┘ │ ├──────────┤
│ free head ┼──┐ │ │ vacant │
├───────────┤ │ │ ╞══════════╡
│ page #2 │ │ │ │ next │
└───────────┘ │ │ ├──────────┤ EBR-protected
... │ │ │generation│ container
... │ │ ├──────────┤ ┌───────────┐
┌───────────┐ │ │ │ occupied ├─────►│ strong │
│ page #M-1 │ │ │ ╞══════════╡ │ reference │
└───────────┘ │ └─┼─ next │ │ counter │
└───►├──────────┤ ├───────────┤
(pages are │generation│ │ │
lazily ├──────────┤ │ value │
allocated) │ vacant │ │ │
└──────────┘ └───────────┘
The size of the first page in a shard is always a power of two, and every subsequent page added after the first is twice as large as the page that precedes it:
pages slots capacity
┌────┐ ┌─┬─┐
│ #0 ├───▶ │x│ 1IPS
├────┤ ├─┼─┼─┬─┐
│ #1 ├───▶ │x│x│ │ 2IPS
├────┤ ├─┼─┼─┼─┼─┬─┬─┬─┐
│ #2 ├───▶ │x│ │x│x│x│ │ │ 4IPS
├────┤ ├─┼─┼─┼─┼─┼─┼─┼─┼─┬─┬─┬─┬─┬─┬─┬─┐
│#M-1├───▶ │ │x│ │x│x│x│ │ │x│ │x│x│x│ │ │ 8IPS
└────┘ └─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┴─┘
where
IPSisConfig::INITIAL_PAGE_SIZE(32 by default)MisConfig::MAX_PAGES(27 by default)xis occupied slots
The Key structure:
Key Structure (64b)
┌──────────┬────────────┬───────────┐
│ reserved │ generation │ page+slot │
│ ≤32b │ ≤32b │ ≤32b │
│ def=0b │ def=32b │ def=32b │
└──────────┴────────────┴───────────┘
Check Config documentation for details how to configure these parts.
Dependencies
~0.1–23MB
~296K SLoC