1 unstable release
| 0.1.0 | Jun 9, 2021 |
|---|
#2038 in Cryptography
295KB
1K
SLoC
HashWires 🐙 :: Range proofs for issued credentials
A Rust implementation of the range proof scheme described in HashWires: Hyperefficient Credential-Based Range Proofs, accepted in Privacy Enhancing Technologies (PETS) 2021 conference, by Konstantinos Chalkias and Shir Cohen and Kevin Lewi and Fredric Moezinia and Yolan Romailler. A more simplified demonstration of how HashWires work is available as a ZKProof blogpost.
HashWires is a hash-based range proof protocol that is applicable in settings for which there is a trusted third party (typically a credential issuer) that can generate commitments. We refer to these as "credential-based" range proofs (CBRPs). It improves upon hashchain solutions that are typically restricted to micro-payments for small interval ranges, achieving an exponential speedup in proof generation and verification time. In terms of proof size and computational cost, we show that HashWires compares favorably against Bulletproofs for both 32- and 64-bit numeric values.
Although CBRPs are inherently less flexible than general zero-knowledge range proofs, we provide a number of applications in which a credential issuer can leverage HashWires to provide range proofs for private values, without having to rely on heavyweight cryptographic tools and assumptions.
Potential Applications:
- KYC range proofs (e.g., older/younger than age proofs)
- 2D/3D location range proofs (you can
- Proof of income (e.g., to landlords) without revealing the exact bank account balance or payslip salary
- Timestamp ranges (e.g, for digital certificates)
- Top % rankings (e.g., online contest ranking)
- % range for ingredients (e.g., in food and chemical products, showing compliance but without revealing the recipe)
- Micro payments (e.g., gradually redeemable cashier checks)
- Auction systems, where bidders want to hide their available funds (as this leaks information on how far they can go)
Note: The commitments used in HashWires are not homomorphic and thus they cannot be used for adding confidential amounts in blockchain applications.
Documentation
Let's assume that Alice is a trusted issuer and Bob is requesting a HashWires commitment for his age (he is 43 years
old). Carol is a verifier, who should be convinced that Bob is older that 21 years. They all agree on a base: u32
which defines how long each hash-chain can be and max_number_bits: usize which denotes the bits of the maximum number
supported in this use case.
Given Bob's age value: BigUint, Alice picks a seed: [u8] and instantiates a Secret for this commitment as
let secret = Secret::<Blake3>::gen(&seed, &value);. The secret can be instantiated with any hash function (in
this example we are using Blake3).
Alice can now generate a commitment by let commitment = secret.commit(base, max_number_bits);. Currently this crate
can only support a base in the set of {2, 4, 16, 256}. If required, a commitment can be serialized using
let commitment_bytes = commitment.serialize(); and it will be provided to Bob (in practice signed by Alice's key).
Bob can now generate a range proof by let proof = secret.prove(base, max_number_bits, &threshold);, where
threshold: BigUint is the challenge (range value) Carol is requesting (thus, 21 in our example).
Given the HashWires commitment and proof, Carol can verify the range proof's statement by
commitment.verify(&proof, &threshold);, which will return a HwError if it fails.
A sample full cycle prove_and_verify test:
// A full HashWires cycle with serialized outputs.
fn prove_and_verify(
base: u32,
max_number_bits: usize,
value: &BigUint,
threshold: &BigUint,
) -> Result<(), HwError> {
// Pick a random 32-byte seed.
let mut rng = OsRng;
let mut seed = vec![0u8; 32];
rng.fill_bytes(&mut seed);
// Generate secret.
let secret = Secret::<Blake3>::gen(&seed, &value);
// Generate and serialize commitment.
let commitment = secret.commit(base, max_number_bits)?;
let commitment_bytes = commitment.serialize();
// Generate and serialize a HashWires proof.
let proof = secret.prove(base, max_number_bits, &threshold)?;
let proof_bytes = proof.serialize();
// Verify a range proof over a commitment.
commitment.verify(&proof, &threshold)?;
Commitment::<Blake3>::deserialize(&commitment_bytes, base)
.verify(&Proof::deserialize(&proof_bytes)?, &threshold)
}
HashWires structure sample
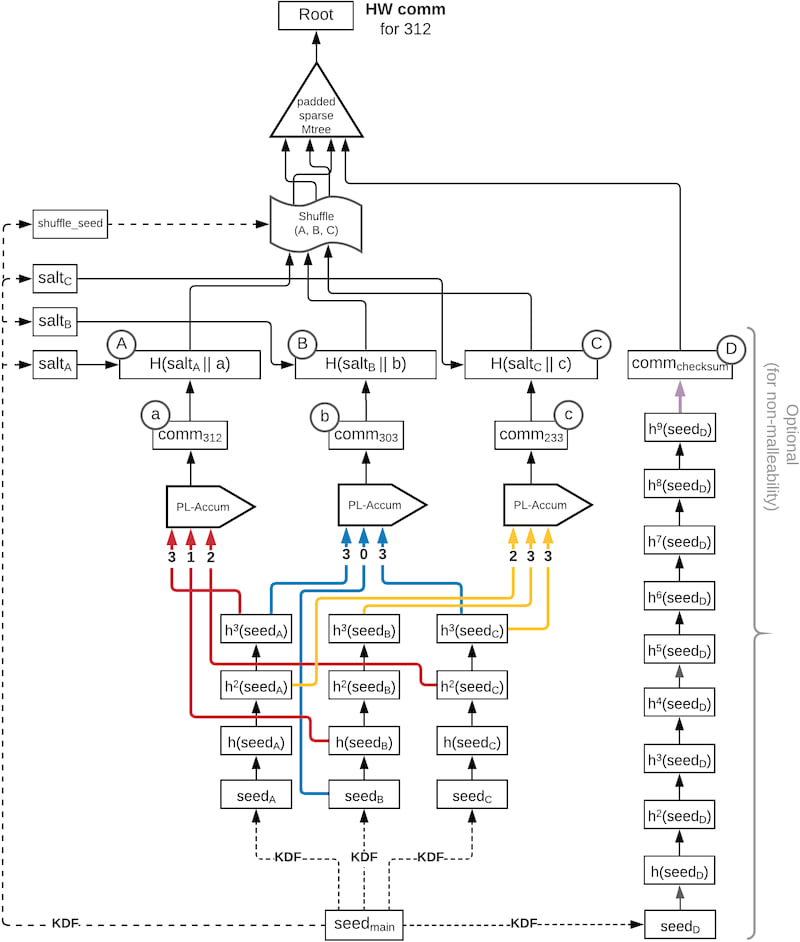 Fig.1 Full snapshot of a HashWires commitment structure for the number 312 in base-4. Note that malleability
protection is work in progress.
Fig.1 Full snapshot of a HashWires commitment structure for the number 312 in base-4. Note that malleability
protection is work in progress.
Performance
The HashWires performance depends on 3 parameters: the selected base, the maximum number supported and the underlying hash function.
The benchmarks were run on a MacBook Pro2.4 GHz 8-Core Intel Core i9 CPU with 32GB or RAM. As shown, Blake3 performs better than SHA2 in our selected Intel CPU, although it’s true that in AMD Ryzen architectures that support SHA extensions BLAKE3 is only slightly faster than hardware-accelerated SHA-256. Another interesting result is that because proof generation internally regenerates the commitment to compute the final tree-inclusion proofs, it is slightly more expensive than commitment creation.
Efficiency comparison (in microseconds) between Bulletproofs with and without AVX2 support, and HashWires for 64-bit integers, different bases and hash functions.
| scheme | Commit gen. | Proof gen. | Proof verify |
|---|---|---|---|
| Bulletproofs | 71 | 12099 | 1555 |
| Bulletproofs AVX2 | 36 | 6516 | 938 |
| HashWires b16 SHA2-256 | 274 | 278 | 84 |
| HashWires b256 SHA2-256 | 651 | 656 | 619 |
| HashWires b16 Blake3 | 101 | 103 | 31 |
| HashWires b256 Blake3 | 260 | 263 | 230 |
Contributors
The original authors of this code are Konstantinos Chalkias (@kchalkias), Kevin Lewi (@kevinlewi) and Yolan Romailler (@AnomalRoil). To learn more about contributing to this project, see this document.
Disclaimers
This software is still evolving and it has not been audited. Use at your own risk.
License
This project is MIT licensed.
Dependencies
~7.5MB
~140K SLoC