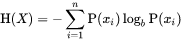2 stable releases
| 1.0.2 | May 6, 2020 |
|---|
#30 in #entropy
19KB
91 lines
entropy
entropy is a tiny utility for calculating Shannon entropy of a given file.
tuxⒶlattice:[~] => ./entropy --help
entropy 1.0.0
tux <me@johnpacific.com>
A utility to calculate Shannon entropy of a given file
USAGE:
entropy [FLAGS] <filepath>
ARGS:
<filepath> The target file to measure
FLAGS:
-h, --help Prints help information
-m, --metric-entropy Returns metric entropy instead of Shannon entropy
-V, --version Prints version information
Usage
To calculate the Shannon entropy of a given file, simply:
tuxⒶlattice:[~] => ./entropy path/to/file.bin
4.142214
To calculate the metric entropy of a given file, add the --metric-entropy flag:
tuxⒶlattice:[~] => ./entropy path/to/file.bin --metric-entropy
0.5177767
What is Shannon entropy?
Shannon entropy can be described as the amount of "information" in a string.
It can be calculated from the following equation:
The output of this equation (when performed in log_2) can tell you the minimum
number of bits required to encode a piece of "information" or "symbol" in binary form.
Metric entropy is calculated by dividing the Shannon entropy with the length of
the symbol. Since we are calculating Shannon entropy in bits (via log_2) and
counting bytes, we divide the Shannon entropy by eight (the number of bits in a byte).
The output of metric entropy is number between 0 and 1, where 1 indicates that the information (or symbols) are uniformly distributed across the string. This can be used to assess how "random" or "uncertain" a particular string is. It can also be an indicator that data may be effectively compressed when metric entropy is closer to 0.
Demonstration
Let's calculate the Shannon entropy and metric entropy of a really random file from /dev/urandom:
tuxⒶlattice:[~] => cat /dev/urandom | head -c 1000000 > random.bin
So we filled a 1MB file of random data from /dev/urandom. The data inside
should be uniformly distributed, but let's verify this:
tuxⒶlattice:[~] => ./entropy random.bin
7.9998097
tuxⒶlattice:[~] => ./entropy random.bin --metric-entropy
0.9999762
As you can see above, the Shannon entropy indicates that we need to encode each
symbol in the file with eight bits. The metric entropy indicates that the information
in the random.bin file is uniformly distributed; it's chock-full of information!
Now what happens if we do the same thing but from a file filled with all zeros? Let's find out:
tuxⒶlattice:[~] => cat /dev/zero | head -c 1000000 > zero.bin
tuxⒶlattice:[~] => ./entropy zero.bin
0
tuxⒶlattice:[~] => ./entropy zero.bin --metric-entropy
0
The Shannon and metric entropy is zero! Why? Because there are no unique symbols in the file. The probability of finding a zero in this file is exactly 1; it's impossible to find a non-zero symbol in the file. Therefore, we don't need any extra information to encode it in a binary sequence.
For more information, see the excellent Wikipedia entry on this topic.
If this repo helped you at all, please reach out and tell me how! I'd love to hear it!
Dependencies
~1.5MB
~24K SLoC