13 releases
| 0.1.12 | Feb 9, 2025 |
|---|---|
| 0.1.11 | Jul 4, 2024 |
| 0.1.10 | Jun 4, 2023 |
| 0.1.3 | May 31, 2023 |
| 0.1.1 | Apr 26, 2023 |
#298 in Algorithms
33 downloads per month
Used in 2 crates
590KB
4K
SLoC
AUTOmata Utilities and Representation (AUTOUR)
The word "Autour" in French refers to a bird. It corresponds to "Goshawk" in English.
Autour is a small toolbox to experiment with various kinds of automata and regular expressions. This project is oriented towards pedagogy rather than performances. It is still a work in progress.
Formalisms
The automata formalisms are the following :
- Deterministic Finite Automata (DFA)
- Nondeterministic Finite Automata (NFA)
- Nondeterministic Finite Automata with Immediate Transitions (NFAIT) (i.e. with epsilon transitions)
- Generalized Nondeterministic Finite Automata (GNFA) with Basic Regular Expressions (BRE) labelling transitions (not yet entirely integrated)
We can also manipulate regular expressions :
- Basic Regular Expressions (BRE)
- Extended Regular Expressions (ERE) (not yet entirely integrated)
Features
Automata can be drawn using GraphViz with the graphviz_dot_builder crate.
In the following we use those graphical representations to introduce some of the features of the toolbox.
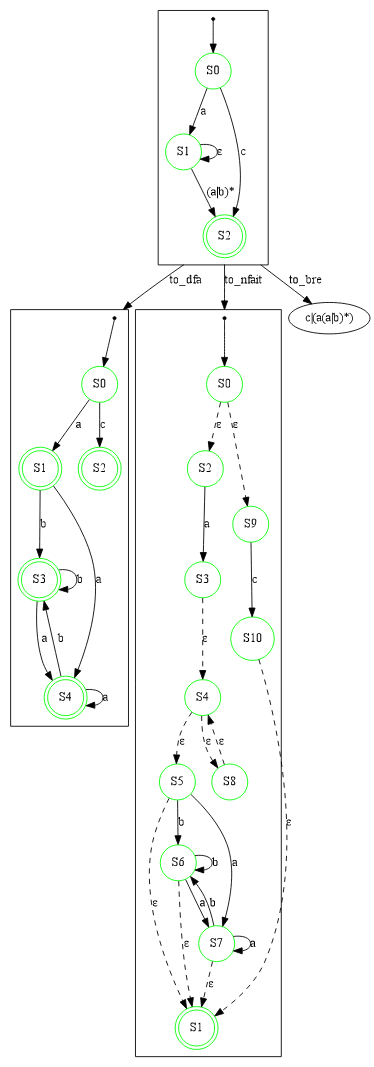
Translations
Translations between the different formalisms is possible. In the example below we translate a GNFA into (from left to right) a DFA, a NFAIT and a BRE.
(Co)-Accessibility
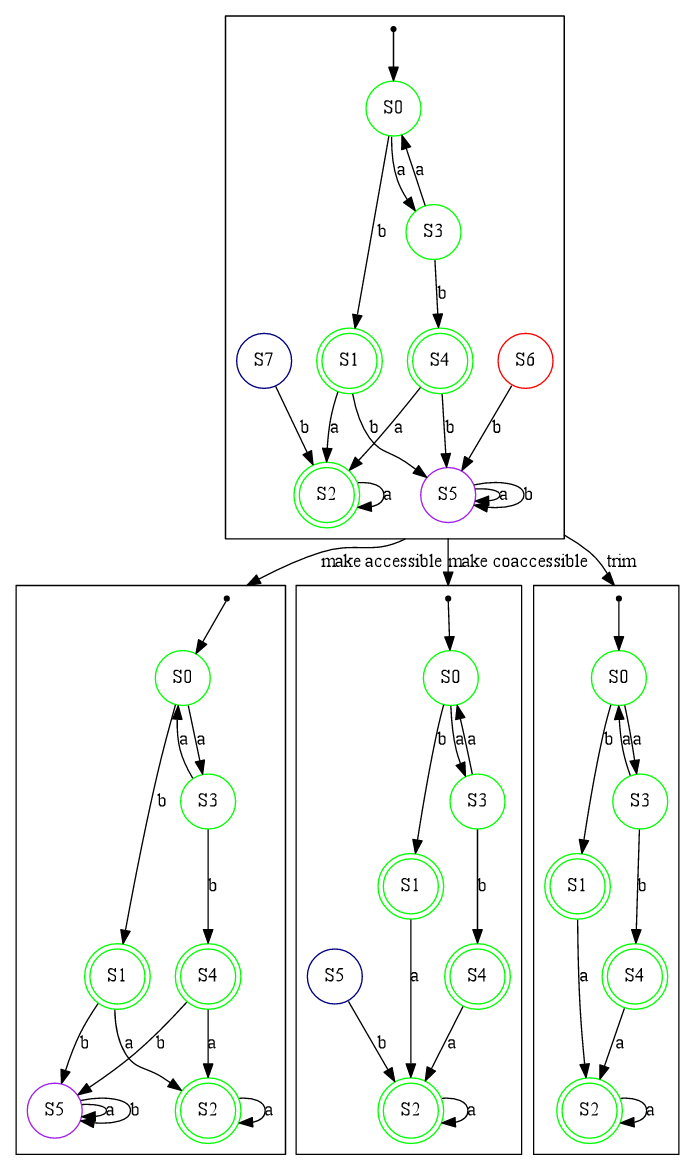
Various algorithms allow:
- determining if an automaton is accessible
- making it accessible
- determining if an automaton is coaccessible
- making it coaccessible
- determining if an automaton is coaccessible
- making it coaccessible
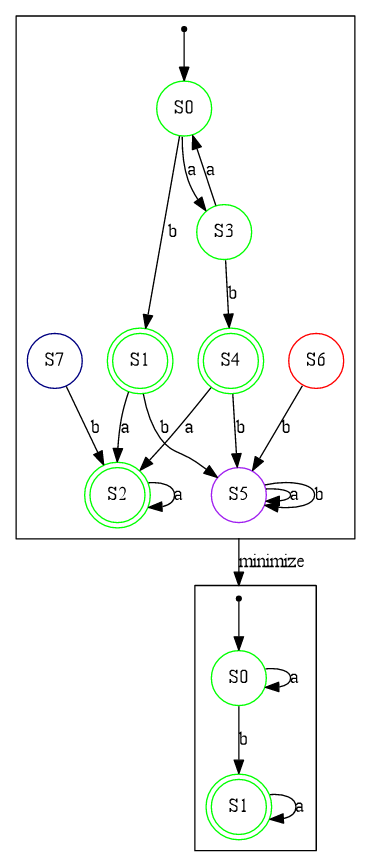
In the example below we have an initial DFA represented at the top of the image.
- The nodes in green are both accessible and coaccessible.
- Those in purple are accessible but not coaccessible.
- Those in blue are coaccessible but not accessible.
- Those in red are neither accessible nor coaccessible.
We then transform this initial DFA (from lef to right):
- by making it accessible
- by making it coaccessible
- by trimming it i.e. making it both accessible and coaccessible
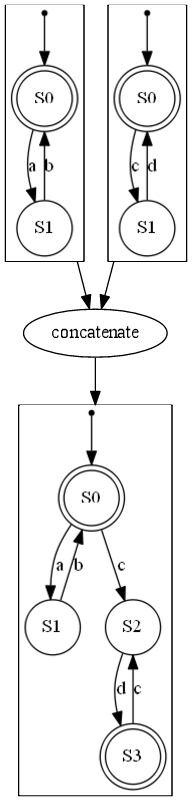
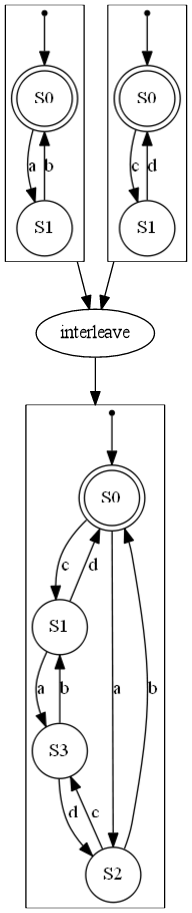
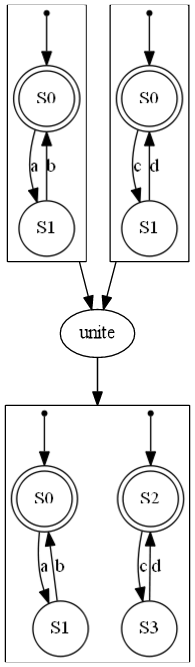
Building Automata
Means to construct terms:
- union
- intersection
- concatenation
- repetition
- negation
- reversion
- etc
See some examples below :
| DFA concatenation | DFA kleene | DFA reverse | DFA interleave | DFA unite |
 |
 |
 |
 |
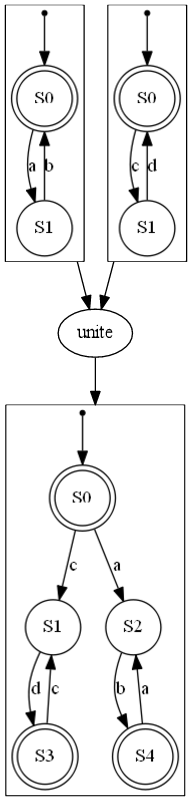 |
| NFA unite | NFA intersection |
 |
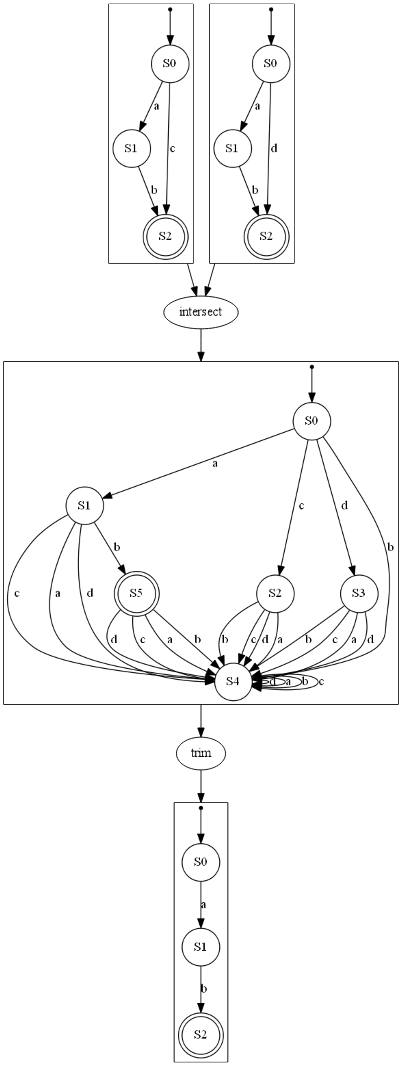 |
Automaton minimization
DFA
DFA minimization is implemented via Brzozowski's algorithm (reverse of the reverse).
Below is an example:
NFA
NFA minimization is implemented via the Kameda-Weiner algorithm. Below are represented two examples detailing the process.
A first example:
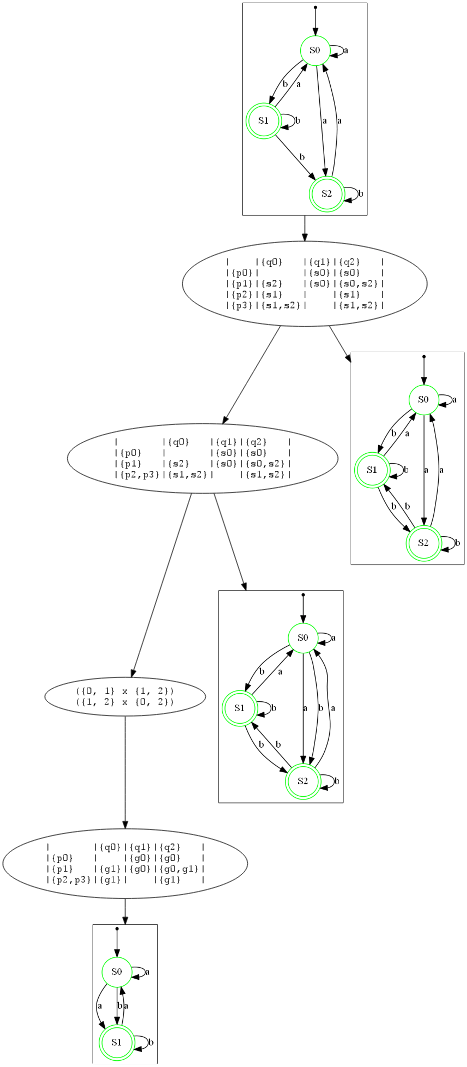
And a second which is a NFA accepting the reverse language w.r.t. the first example (you can notice the symmetry of matrices between the two examples modulo rows and columns positions substitution):
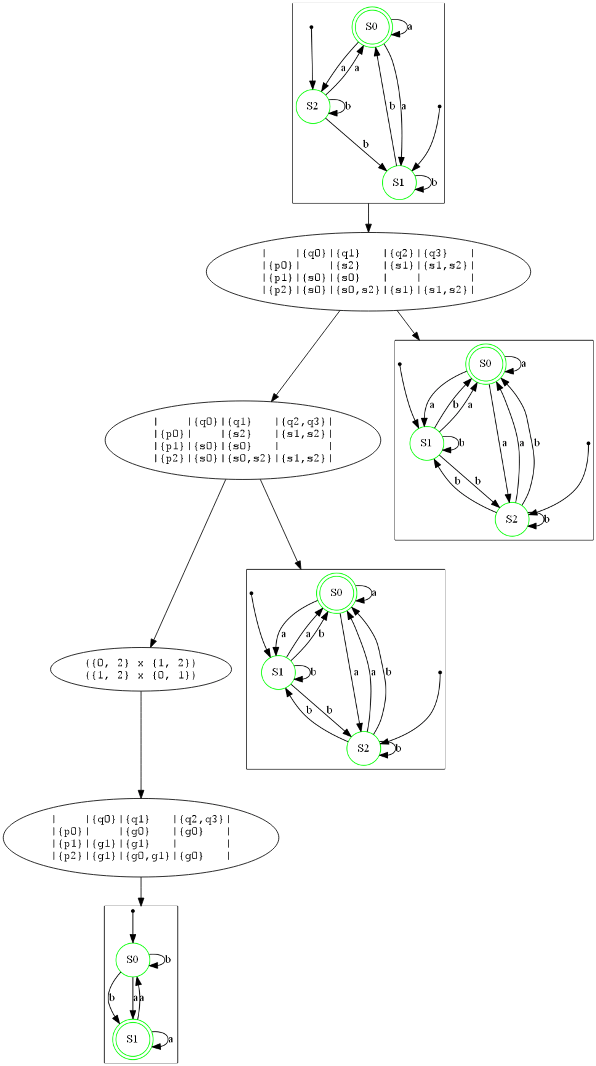
Alphabet hiding and substitution
Another thing that we can do is substitute letters or hide them.
In the example below we have an initial GNFA drawn at the top of the image. Then, from left to right:
- we hide letter 'b' in it
- we substitute letter 'b' by letter 'c' in it
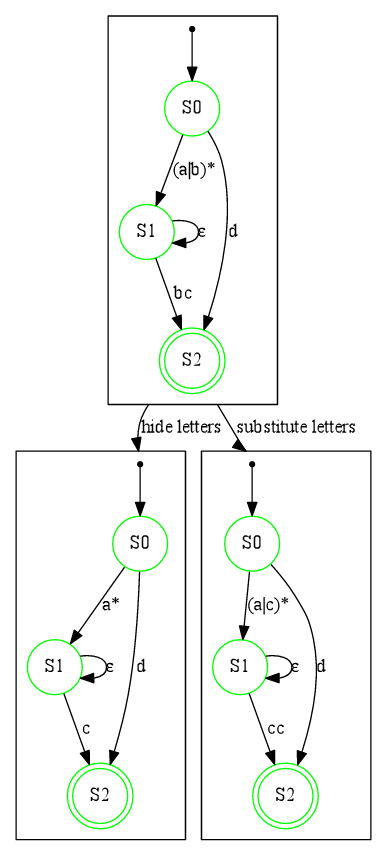
Other features
- completion up to alphabet
- running transitions and traces in DFA/NFA
- etc
Dependencies
~1.1–1.7MB
~35K SLoC